Minggu lepas, kami telah memperkenalkanPengurusan Risiko VaRApabila bercakap tentang risiko portfolio, ia tidak sama dengan risiko setiap aset individu, tetapi berkaitan dengan korelasi harga mereka. Mengambil dua aset sebagai contoh, jika korelasi positifnya sangat kuat, iaitu, ia naik dan turun bersama-sama, maka mempelbagaikan pelaburan yang panjang tidak akan mengurangkan risiko Jika korelasi negatif sangat kuat, kepelbagaian boleh mengurangkan risiko dengan ketara. Persoalan semula jadi ialah, apabila melabur dalam portfolio, bagaimana anda memaksimumkan pulangan pada tahap risiko tertentu? Di sinilah teori Markowitz, yang akan saya perkenalkan hari ini, berlaku.

Teori Portfolio Moden (MPT), yang dicadangkan oleh Harry Markowitz pada tahun 1952, ialah rangka kerja matematik untuk pemilihan portfolio yang bertujuan untuk memaksimumkan pulangan yang dijangkakan dengan memilih kombinasi aset berisiko yang berbeza sambil mengawal risiko. Idea teras ialah harga aset tidak bergerak dalam penyegerakan sempurna (iaitu, terdapat korelasi yang tidak sempurna antara aset), dan risiko pelaburan keseluruhan boleh dikurangkan dengan mempelbagaikan peruntukan aset.

Konsep Utama Teori Markowitz

1. Kadar pulangan yang dijangkakan: Ini ialah pulangan yang boleh diharapkan oleh pelabur untuk memperoleh dengan memegang aset atau portfolio, biasanya diramalkan berdasarkan data pulangan sejarah.

\(E(R_p) = \sum_{i=1}^{n} w_i E(R_i)\)

Di mana \(E(R_p)\) ialah kadar pulangan yang dijangkakan bagi portfolio, \(wi\) ialah berat aset \(i\)th dalam portfolio dan \(E(R_i)\) ialah kadar pulangan yang dijangkakan bagi \( Aset ke \)i.

1. Risiko (kemeruapan atau sisihan piawai): Digunakan untuk mengukur ketidakpastian pulangan pelaburan atau turun naik sesuatu pelaburan.

\(\sigma_p = \sqrt{\sum_{i=1}^{n} \sum_{j=1}^{n} w_i w_j \sigma_{ij}}\)

Di mana \(\sigma_p\) ialah jumlah risiko portfolio dan \(\sigma_{ij}\) ialah kovarians antara aset \(i\) dan aset \(j\), yang mengukur hubungan antara perubahan harga kedua-dua aset.

1. Kovarians: Mengukur korelasi antara pergerakan harga dua aset.

\(\sigma_{ij} = \rho_{ij} \sigma_i \sigma_j\)

Di mana \(\rho_{ij}\) ialah pekali korelasi antara aset \(i\) dan aset \(j\), \(\sigma_i\) dan \(\sigma_j\) ialah sisihan piawai aset \(i\) dan aset \(j\) masing-masing.

1. Frontier Cekap: Dalam sistem koordinat pulangan-risiko, sempadan cekap ialah set portfolio yang boleh memberikan pulangan maksimum yang dijangkakan pada tahap risiko tertentu.

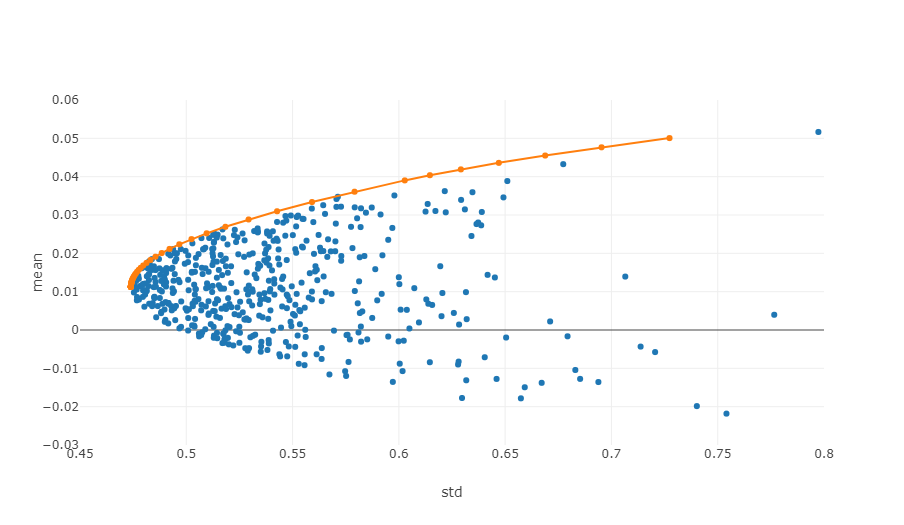
Gambar di atas ialah gambarajah skema bagi sempadan berkesan Setiap titik mewakili portfolio pelaburan dengan berat yang berbeza Paksi mendatar ialah turun naik, iaitu, tahap risiko, dan paksi menegak ialah kadar pulangan. Jelas sekali, kami menumpukan pada tepi atas graf, yang mencapai pulangan tertinggi pada tahap risiko yang sama.

Dalam perdagangan kuantitatif dan pengurusan portfolio, menggunakan prinsip ini memerlukan analisis statistik data sejarah dan penggunaan model matematik untuk menganggarkan pulangan yang dijangka, sisihan piawai dan kovarians pelbagai aset. Kemudian, teknik pengoptimuman digunakan untuk mencari konfigurasi berat aset yang terbaik. Proses ini biasanya melibatkan pengiraan matematik yang kompleks dan banyak pemprosesan komputer, itulah sebabnya analisis kuantitatif telah menjadi sangat penting dalam kewangan moden. Berikut akan menggunakan contoh Python khusus untuk menggambarkan cara mengoptimumkan.

Contoh kod Python untuk mencari kombinasi optimum menggunakan kaedah simulasi

Pengiraan portfolio optimum Markowitz ialah proses berbilang langkah yang melibatkan beberapa langkah utama seperti penyediaan data, simulasi portfolio dan pengiraan penunjuk. Rujukan: https://plotly.com/python/v3/ipython-notebooks/markowitz-portfolio-optimization/

1. Dapatkan data pasaran：

   • lulusget_dataBerfungsi untuk mendapatkan data harga sejarah mata wang digital yang dipilih. Ini adalah data yang diperlukan untuk mengira kadar pulangan dan risiko, yang digunakan untuk membina portfolio dan mengira nisbah Sharpe.

2. Mengira Pulangan dan Risiko：

   • gunacalculate_returns_riskFungsi ini mengira kadar pulangan tahunan dan risiko tahunan (sisihan piawai) untuk setiap mata wang digital. Ini adalah untuk mengukur prestasi sejarah setiap aset untuk digunakan dalam portfolio yang optimum.

3. Kira portfolio optimum Markowitz：

   • gunacalculate_optimal_portfolioBerfungsi, mensimulasikan pelbagai portfolio. Dalam setiap simulasi, wajaran aset dijana secara rawak dan jangkaan pulangan dan risiko portfolio kemudiannya dikira berdasarkan wajaran ini.
   • Dengan menjana gabungan berat yang berbeza secara rawak, pelbagai portfolio yang mungkin boleh diterokai untuk mencari kombinasi terbaik. Ini adalah salah satu idea teras teori portfolio Markowitz.

Matlamat keseluruhan proses adalah untuk mencari portfolio yang memberikan pulangan jangkaan terbaik untuk tahap risiko tertentu. Dengan mensimulasikan berbilang kombinasi yang mungkin, pelabur boleh memahami dengan lebih baik prestasi konfigurasi yang berbeza dan memilih gabungan yang paling sesuai dengan objektif pelaburan dan toleransi risiko mereka. Pendekatan ini membantu mengoptimumkan keputusan pelaburan dan menjadikan pelaburan lebih cekap.

import numpy as np
import pandas as pd
import requests
import matplotlib.pyplot as plt

# 获取行情数据
def get_data(symbols):
    data = []
    for symbol in symbols:
        url = 'https://api.binance.com/api/v3/klines?symbol=%s&interval=%s&limit=1000'%(symbol,'1d')
        res = requests.get(url)
        data.append([float(line[4]) for line in res.json()])
    return data

def calculate_returns_risk(data):
    returns = []
    risks = []

    for d in data:
        daily_returns = np.diff(d) / d[:-1]
        annualized_return = np.mean(daily_returns) * 365
        annualized_volatility = np.std(daily_returns) * np.sqrt(365)

        returns.append(annualized_return)
        risks.append(annualized_volatility)

    return np.array(returns), np.array(risks)

# 计算马科维茨最优组合
def calculate_optimal_portfolio(returns, risks):
    n_assets = len(returns)
    num_portfolios = 3000

    results = np.zeros((4, num_portfolios), dtype=object) 


    for i in range(num_portfolios):
        weights = np.random.random(n_assets)
        weights /= np.sum(weights)

        portfolio_return = np.sum(returns * weights)
        portfolio_risk = np.sqrt(np.dot(weights.T, np.dot(np.cov(returns, rowvar=False), weights)))

        results[0, i] = portfolio_return
        results[1, i] = portfolio_risk
        results[2, i] = portfolio_return / portfolio_risk
        results[3, i] = list(weights) # 将权重转换为列表

    return results

symbols = ['BTCUSDT','ETHUSDT', 'BNBUSDT','LINKUSDT','BCHUSDT','LTCUSDT']
data = get_data(symbols)

returns, risks = calculate_returns_risk(data)
optimal_portfolios = calculate_optimal_portfolio(returns, risks)

max_sharpe_idx = np.argmax(optimal_portfolios[2])
optimal_return = optimal_portfolios[0, max_sharpe_idx]
optimal_risk = optimal_portfolios[1, max_sharpe_idx]
optimal_weights = optimal_portfolios[3, max_sharpe_idx]

# 输出结果
print("最优组合:")
for i in range(len(symbols)):
    print(f"{symbols[i]}权重: {optimal_weights[i]:.4f}")

print(f"预期收益率: {optimal_return:.4f}")
print(f"预期风险(标准差): {optimal_risk:.4f}")
print(f"夏普比率: {optimal_return / optimal_risk:.4f}")

# 可视化投资组合
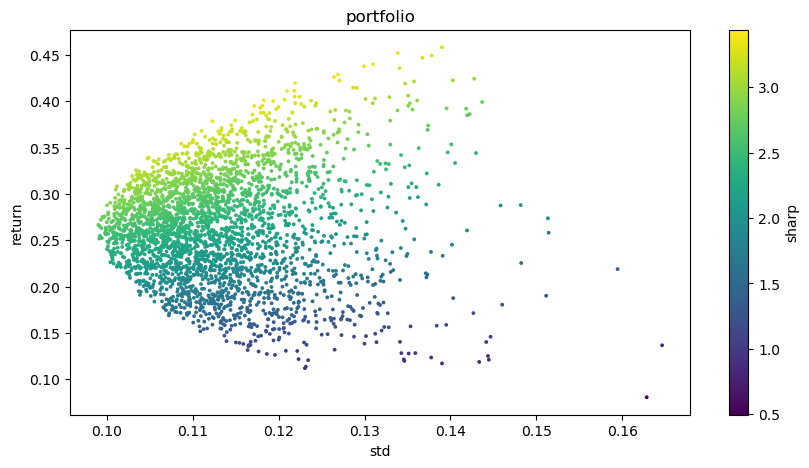
plt.figure(figsize=(10, 5))
plt.scatter(optimal_portfolios[1], optimal_portfolios[0], c=optimal_portfolios[2], marker='o', s=3)
plt.title('portfolio')
plt.xlabel('std')
plt.ylabel('return')
plt.colorbar(label='sharp')
plt.show()

Keluaran akhir: Gabungan terbaik: Berat BTCUSDT: 0.0721 Berat ETHUSDT: 0.2704 Berat BNBUSDT: 0.3646 Berat LINKUSDT: 0.1892 Berat BCHUSDT: 0.0829 Berat LTCUSDT: 0.0209 Kadar pulangan yang dijangkakan: 0.4195 Jangkaan risiko (sisihan piawai): 0.1219 Nisbah Sharpe: 3.4403