Strategi dagangan dalam hari yang menggunakan pengembalian nilai rata antara SPY dan IWM

Dalam artikel ini, kita akan menulis strategi dagangan dalam sehari. Ia akan menggunakan konsep dagangan klasik iaitu pasangan dagangan yang mempunyai nilai balik yang sama. Dalam contoh ini, kita akan menggunakan dua dana indeks terbuka (ETF), SPY dan IWM yang berdagang di Bursa Saham New York (NYSE) dan cuba mewakili indeks pasaran saham Amerika Syarikat, iaitu S&P 500 dan Russell 2000.

Strategi ini mewujudkan perbezaan keuntungan dengan melakukan lebih daripada satu ETF dan tidak melakukan satu lagi ETF. Perbandingan banyak ruang boleh ditakrifkan dalam banyak cara, seperti menggunakan kaedah siri masa penyatuan statistik. Dalam keadaan ini, kita akan mengira nisbah perhadangan antara SPY dan IWM melalui regresi linear bergolak. Ini akan membolehkan kita membuat perbezaan keuntungan antara SPY dan IWM, yang ditandaskan sebagai z-score. Apabila z-score melebihi satu ambang, isyarat perdagangan akan dihasilkan kerana kita percaya bahawa perbezaan keuntungan akan kembali ke purata.

Prinsip asas strategi ini adalah bahawa SPY dan IWM mewakili keadaan pasaran yang sama, iaitu prestasi harga saham sekumpulan syarikat besar dan kecil di Amerika Syarikat. Dengan asumsi bahawa jika harga yang diterima dengan teori regression regression, maka ia akan selalu kembali, kerana peristiwa regression mungkin mempengaruhi S&P 500 dan Russell 2000 dalam masa yang sangat singkat, tetapi perbezaan keuntungan antara mereka akan selalu kembali ke purata normal, dan kedua-dua urutan harga jangka panjang akan selalu disatukan.

Strategi

Strategi ini dilaksanakan dengan langkah-langkah berikut:

Data - 1 minit grafik k dari SPY dan IWM diperoleh dari April 2007 hingga Februari 2014.

Mengolah - menyusun data dengan betul dan memadamkan k-string yang saling hilang.

Perbezaan - nisbah pegangan antara dua ETF menggunakan pengiraan regresi linear bergolak. Ditakrifkan sebagai pekali regresi β menggunakan tetingkap regresi yang bergerak ke hadapan 1 akar k dan menghitung semula pekali regresi. Oleh itu, nisbah pegangan βi, akar K adalah dengan mengira titik melintasi dari bi-1-k ke bi-1, untuk digunakan untuk membalikkan k baris.

Z-Score - Nilai selisih standard dikira dengan cara biasa. Ini bermaksud mengurangkan rata-rata selisih standard (sampel) dan mengurangkan selisih standard (sampel). Alasan untuk melakukan ini adalah untuk memudahkan parameter ambang untuk difahami, kerana Z-Score adalah kuantiti tanpa dimensi.

Perdagangan - apabila nilai z-score negatif jatuh di bawah ambang yang ditetapkan (atau optimum selepas itu), isyarat melakukan lebih banyak, sedangkan isyarat tidak dilakukan sebaliknya. Apabila nilai mutlak z-score jatuh di bawah ambang tambahan, isyarat rata akan dihasilkan. Untuk strategi ini, saya (agak rawak) memilih z-score = 2 sebagai ambang perdagangan terbuka, dan z-score = 1 sebagai ambang perdagangan rata.

Mungkin cara terbaik untuk memahami strategi dengan lebih mendalam adalah dengan mengimplementasikannya secara praktikal. Bahagian berikut menerangkan secara terperinci kod Python yang lengkap untuk melaksanakan strategi pengembalian nilai rata ini ("fail tunggal"). Saya telah menambah nota kod terperinci untuk membantu anda memahami lebih baik.

Pelaksanaan Python

Seperti semua tutorial Python/pandas, ia mesti disiapkan mengikut persekitaran Python yang diterangkan dalam tutorial ini. Setelah persediaan selesai, tugas pertama adalah mengimport perpustakaan Python yang diperlukan. Ini diperlukan untuk menggunakan matplotlib dan pandas.

Di bawah ini adalah versi perpustakaan khusus yang saya gunakan:

Python - 2.7.3 NumPy - 1.8.0 panda - 0.12.0 Matplotlib - 1.1.0

Mari kita teruskan dan masukkan perpustakaan ini:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Fungsi create_pairs_dataframe berikut akan mengimport dua fail CSV k dalam talian yang mengandungi dua simbol. Dalam contoh kami, ini akan menjadi SPY dan IWM. Kemudian ia akan membuat pasangan data yang berasingan, yang akan menggunakan indeks kedua-dua fail asal.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Langkah seterusnya ialah melakukan regresi linear bergolak antara SPY dan IWM. Dalam kes ini, IWM adalah peramal (x) dan SPY adalah tindak balas (y). Saya menetapkan tetingkap regresi lalai dengan 100 baris k. Seperti yang dinyatakan di atas, ini adalah parameter untuk dasar. Untuk menjadikan dasar dianggap kukuh, kita secara ideal ingin melihat laporan yang dikembalikan menunjukkan keadaan fungsi konkrit (x) atau prestasi lain pada tempoh regresi. Oleh itu, pada peringkat akhir kod, kita akan melakukan analisis sensitiviti melalui tempoh regresi dalam jangka perubahan.

Selepas mengira penganjur beta dalam model regresi linear SPY-IWM, tambahkan kepada pasangan DataFrame dan hapus baris kosong. Ini membina kumpulan K baris pertama, yang sama dengan metrik pemangkasan panjang regresi. Kemudian, kami mencipta dua margin ETF, masing-masing unit SPY dan unit -βi IWM. Jelasnya, ini bukan keadaan yang realistik kerana kita menggunakan sejumlah kecil IWM, yang tidak mungkin dalam pelaksanaan sebenar.

Akhirnya, kita mencipta z-score perbezaannya dengan mengurangkan purata perbezaannya dan mengira standard perbezaannya dengan standard perbezaannya. Perlu diperhatikan bahawa terdapat perbezaannya yang agak halus di sini. Saya sengaja menyimpannya dalam kod kerana saya ingin menekankan betapa mudahnya melakukan kesilapan seperti itu dalam kajian. Mengira purata dan standard perbezaannya untuk keseluruhan rentetan masa perbezaannya.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Dalam create_long_short_market_signals, isyarat dagangan dicipta. Ini dikira dengan nilai z-score melebihi ambang. Isyarat penempatan diberikan apabila nilai mutlak z-score kurang daripada atau sama dengan ambang lain.

Untuk mencapai keadaan ini, adalah perlu untuk menetapkan strategi perdagangan untuk setiap baris k yang terbuka atau kosong. Long_market dan short_market adalah dua pembolehubah yang ditakrifkan untuk mengesan kedudukan multihead dan kosong. Malangnya, ia lebih mudah untuk diprogramkan secara berulang berbanding dengan kaedah kuantifikasi, dan oleh itu ia agak perlahan. Walaupun grafik baris k 1 minit memerlukan kira-kira 700,000 titik data untuk setiap fail CSV, ia masih agak cepat dikira pada desktop lama saya!

Untuk mengulangi satu DataFrame panda (yang pastinya merupakan operasi yang tidak biasa), adalah perlu untuk menggunakan kaedah iterrows, yang menyediakan penjana pengulangan:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Pada peringkat ini, kami telah mengemas kini pasangan untuk mengandungi isyarat berbilang, kosong yang sebenarnya, yang membolehkan kami menentukan sama ada kami perlu membuka dagangan. Sekarang kami perlu membuat portfolio untuk mengesan nilai pasaran kedudukan. Tugas pertama adalah untuk membuat barisan kedudukan yang menggabungkan isyarat berbilang dan isyarat kosong. Ini akan mengandungi satu barisan elemen dari ((1, 0, -1), di mana 1 mewakili kedudukan berbilang, 0 mewakili kedudukan tidak berbilang (harus rata), dan -1 mewakili kedudukan kosong.

Setelah nilai pasaran ETF dicipta, kami mengumpulnya untuk menghasilkan nilai pasaran keseluruhan pada akhir setiap baris k. Kemudian kami menukarnya kepada nilai pulangan melalui kaedah pct_change untuk objek itu. Baris kod berikutnya membersihkan entri yang salah ((NaN dan elemen inf) dan akhirnya mengira kurva faedah yang lengkap.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Fungsi utama menggabungkannya. Dalam hari ini, fail CSV terletak di laluan datadir. Pastikan anda mengubah kod berikut untuk mengarahkan direktori tertentu kepada anda.

Untuk menentukan tahap sensitiviti strategi terhadap kitaran lookback, adalah perlu untuk mengira beberapa penunjuk prestasi lookback. Saya memilih peratusan pulangan keseluruhan portfolio sebagai penunjuk prestasi dan rentang lookback[50,200], dengan peningkatan sebanyak 10.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

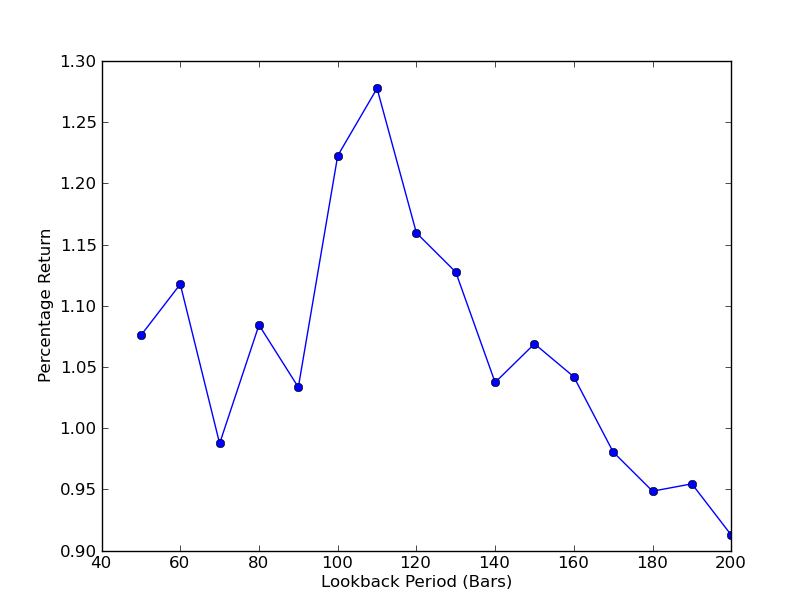
Sekarang anda boleh melihat grafik tentang lookbacks dan returns. Perhatikan bahawa lookback mempunyai nilai maksimum yang setara dengan 110 garis k. Jika kita melihat keadaan yang tidak berkaitan dengan lookbacks dan returns, ini kerana:

SPY-IWM analisis sensitiviti jangkaan linear regression hedging berbanding lookback

Tanpa kurva keuntungan yang miring ke atas, mana-mana artikel ulasan tidak lengkap! Oleh itu, jika anda ingin melukis kurva pulangan keuntungan kumulatif dengan masa, anda boleh menggunakan kod berikut. Ia akan melukis portfolio akhir yang dihasilkan dari kajian parameter pandangan. Oleh itu, adalah perlu untuk memilih pandangan berdasarkan carta yang anda ingin memvisualisasikan. Carta ini juga melukis pulangan SPY untuk tempoh yang sama untuk membantu perbandingan:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Jadual hak dan faedah di bawah adalah 100 hari:

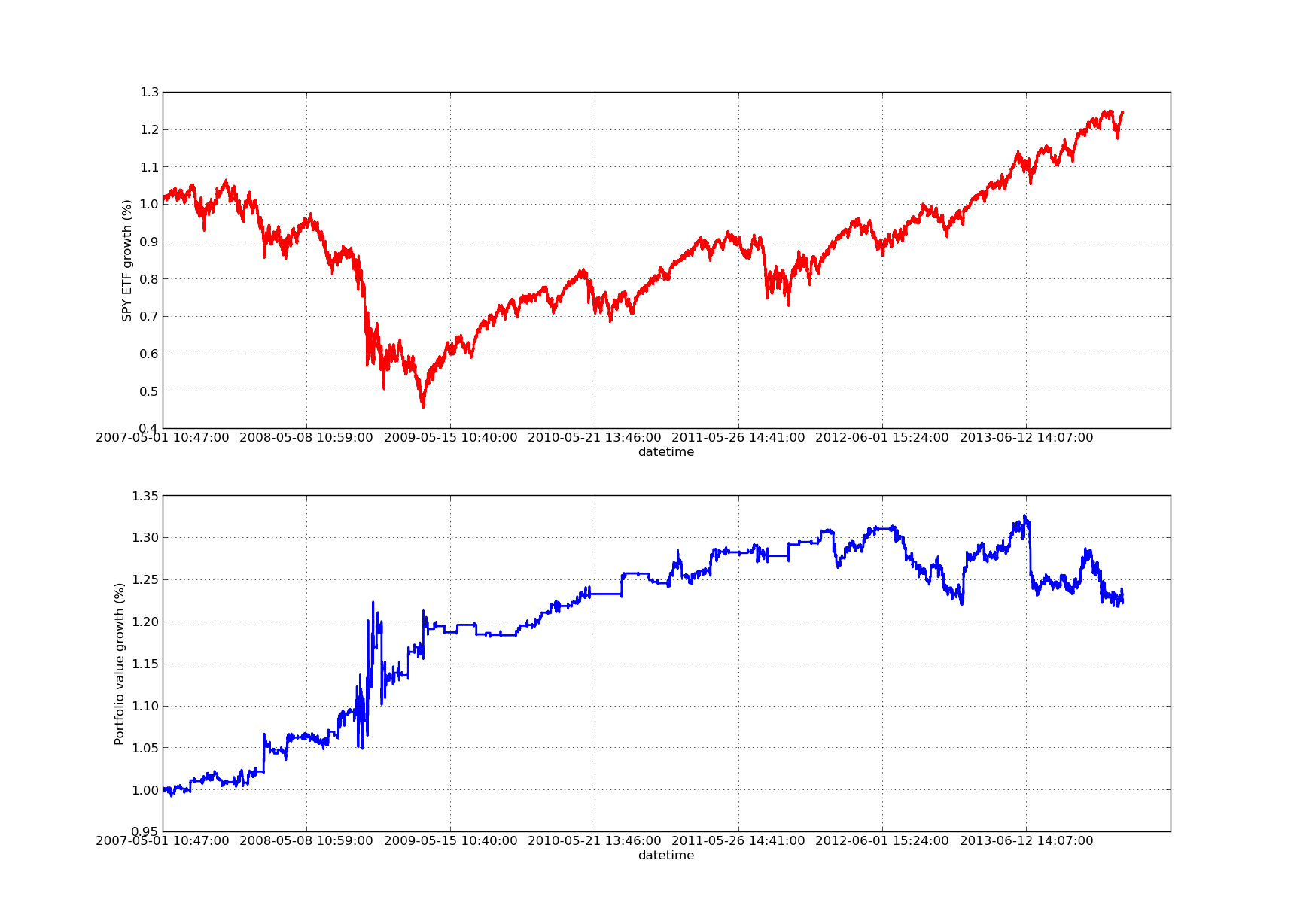
SPY-IWM analisis sensitiviti jangkaan linear regression hedging berbanding lookback

Sila ambil perhatian bahawa SPY 2009 telah mengalami penyusutan yang besar semasa krisis kewangan. Strategi ini juga berada dalam tempoh yang bergolak pada peringkat ini. Sila ambil perhatian juga bahawa prestasi tahun lepas telah merosot kerana sifat SPY yang kuat pada masa ini mencerminkan indeks S&P 500.

Perhatikan bahawa kita masih perlu mempertimbangkan bias bias jangka panjang ketika mengira margin z-score. Selain itu, semua perhitungan ini dilakukan tanpa kos dagangan. Sekali faktor-faktor ini diambil kira, strategi ini pasti akan menunjukkan prestasi yang buruk. Kos prosedur dan titik geser tidak diketahui pada masa ini.

Dalam artikel yang akan datang, kami akan mencipta backtester yang didorong oleh peristiwa yang lebih kompleks yang akan mengambil kira faktor-faktor di atas, yang akan memberi kami lebih keyakinan dalam kurva dana dan penunjuk prestasi.