Vamos falar sobre como otimizar os parâmetros de vários modelos de negociação programática

• #### Altos Parametrais e Ilhas Parametrais

　 Um princípio importante na otimização de parâmetros é a busca de elevações de parâmetros em vez de ilhas de parâmetros. A chamada elevação de parâmetros significa que há um alcance mais amplo de parâmetros, e o modelo obtém melhores resultados dentro desse alcance de parâmetros, geralmente formando uma distribuição quase normal com o centro da elevação. A chamada ilha de parâmetros significa que o modelo só tem um bom desempenho quando o valor do parâmetro está em um pequeno intervalo, e o desempenho do modelo é significativamente alterado quando o parâmetro se desvia desse valor.

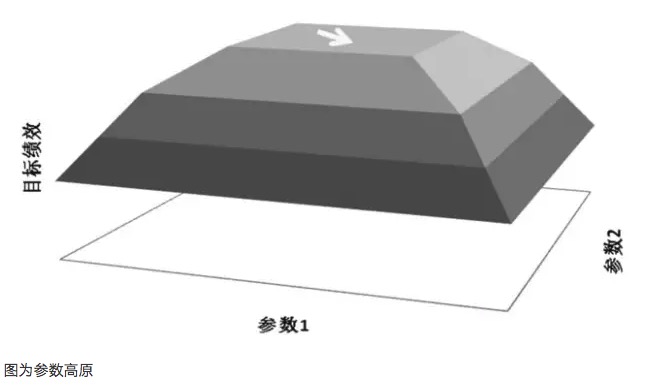
• #### Planalto com parâmetros

Por exemplo, se um modelo de negociação tiver dois parâmetros, o parâmetro 1 e o parâmetro 2, quando os dois parâmetros são testados em roteamento, um gráfico de desempenho tridimensional é obtido. Uma boa distribuição de parâmetros deve ser o gráfico de alta localização dos parâmetros, mesmo que as configurações dos parâmetros sejam desviadas, o desempenho lucrativo do modelo ainda pode ser garantido.

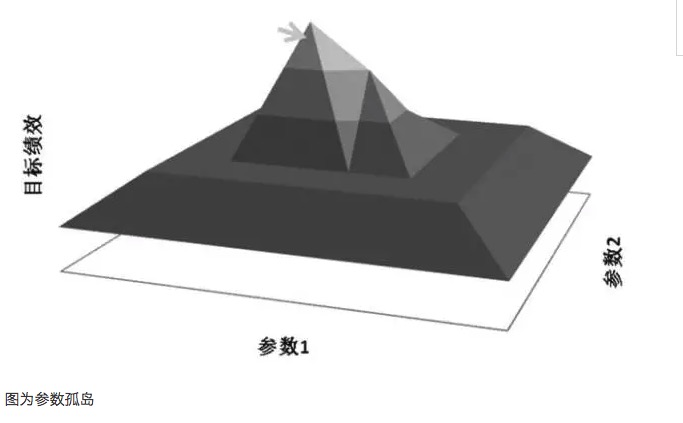
Em geral, se a performance de um sistema de parâmetros próximos é muito diferente da do parâmetro ótimo, então esse parâmetro ótimo pode ser o resultado de uma supersumação, que matematicamente pode ser considerada uma solução singular, e não a solução de valor máximo a ser procurada. Do ponto de vista matemático, a singularidade é instável e, em situações de incerteza futura, o parâmetro ótimo pode se tornar o parâmetro pior, uma vez que as características do mercado mudem.

O excesso de adequação está relacionado à amostra selecionada. Se a amostra selecionada não é representativa da característica geral do mercado, ajuste os parâmetros apenas para que o resultado do teste atinja o valor esperado positivo, o que é sem dúvida uma auto-ilusão. O valor do parâmetro obtido é o parâmetro inválido do excesso de adequação.

A principal contradição entre a superação e a otimização de parâmetros é que o parâmetro ideal obtido com a otimização de parâmetros de modelo é baseado apenas em amostras de dados históricos que já ocorreram, enquanto o comportamento futuro é dinâmico, com semelhanças e variações em relação ao comportamento histórico. O criador do modelo pode encontrar o parâmetro do modelo que melhor desempenhou o modelo historicamente, mas esse parâmetro não é necessariamente o melhor desempenho do modelo no uso real do modelo no futuro, muito menos o melhor desempenho histórico do parâmetro do modelo, que pode ser um parâmetro de péssimo desempenho em uma batalha do modelo no futuro, ou até mesmo trazer grandes perdas. Por exemplo, selecionar um parâmetro que pode capturar uma grande onda de eventos históricos, mas configurar um modelo com esse parâmetro não significa que o modelo também possa ter um bom desempenho na batalha do futuro.

Além disso, o alto patamar de parâmetros e o isolamento de parâmetros também tendem a ter uma grande relação com o número de transações. Se o número de transações do modelo é menor, geralmente é possível encontrar um ponto de parâmetro apropriado, fazendo com que o modelo ganhe em todas as transações, o lucro do modelo após a otimização desses parâmetros reflete uma forte casualidade. Se o número de transações do modelo for maior, a casualidade do lucro do modelo diminuirá, refletindo mais a necessidade e a regularidade do lucro, também haverá um alto patamar de parâmetros.

• #### Método para otimizar os parâmetros

Depois de conhecer os altiplãs e ilhas de parâmetros, o método de otimização de parâmetros é muito importante, especialmente quando há vários parâmetros no modelo (chamados de arquivos de parâmetros), muitas vezes o valor de um parâmetro afeta a distribuição do altiplã de outro parâmetro. Então, como otimizar o conjunto de parâmetros?

Um método é o de convergência gradual. Em primeiro lugar, otimizar um parâmetro individualmente, fixando-o após o seu melhor valor, e depois otimizar outro parâmetro, fixando-o após o seu melhor valor. Assim, o ciclo de seleção continua até que o resultado da otimização não mude. Por exemplo, um modelo de negociação de compra e venda de cruzamento linear, com dois parâmetros independentes, respectivamente, são o ciclo curto N1 e o ciclo longo N2.

Outro método é usar uma plataforma de design de software programado com funções de computação mais poderosas para calcular diretamente a distribuição entre a função-alvo e o conjunto de parâmetros, em seguida, procurar a distribuição de diferença multidimensional e definir um limite de diferença, cujo valor absoluto de diferença seja menor que o correspondente tamanho multidimensional máximo, o maior raio de corte interdimensional, selecionado como o valor de parâmetro mais estável.

Além do método de otimização de parâmetros, a seleção de amostras de dados também é um fator importante. Os modelos que seguem a tendência como ideias de negociação funcionam melhor em situações de tendência, e as estratégias que vendem alto e baixo como ideias de negociação funcionam melhor em situações de oscilação. Portanto, na otimização de parâmetros, é necessário eliminar adequadamente os comportamentos que correspondem às ideias de negociação para considerar o lucro e aumentar os dados de comportamentos que não correspondem à estratégia para considerar os prejuízos.

Por exemplo, os futuros de índices de ações, desde o início de 2010 e até o final de 2014, quando surgiram situações extremas no mercado de touros, foram unilaterais. Sem dúvida, todos os modelos de tendência obtiveram bons resultados. No entanto, se também inserirmos esses dados de tendências extremas na amostra para otimização de parâmetros, os parâmetros do modelo obtido não serão necessariamente os melhores.

Por exemplo, se um modelo tem dois parâmetros, o parâmetro A tem um resultado muito bom em um único período de tempo e um bom desempenho em outros períodos; o outro parâmetro B tem um resultado pior em um único período de tempo e um bom desempenho em outros períodos, e a distribuição entre os períodos é mais uniforme do que o parâmetro A. Mesmo que o parâmetro A tenha um indicador composto de testes em toda a amostra de dados, como o risco de ganho é maior do que o parâmetro B, preferimos o parâmetro B, pois o parâmetro B é mais estável e não depende de uma amostra específica.

Em suma, ao construir modelos de negociação programada, por um lado, pode-se melhorar o modelo por meio da otimização de parâmetros, para que o modelo se adapte melhor aos padrões de flutuação de preços, aumentando o retorno do investimento; Por outro lado, deve-se evitar a adaptação excessiva à otimização de parâmetros, o que reduz significativamente a adaptabilidade do modelo às mudanças de mercado.

Transcrição feita por Programmable Trader