Razão de Sharpe 0,6, devo abandoná-la?

Nós fizemos um experimento para ilustrar este problema. Este experimento começou com algumas hipóteses-chave. Nós temos 20 sinais de negociação com um rendimento anual composto de 8%, com uma taxa anual de Sharpe de 0,6. Os sinais de negociação para esta estratégia não são muito produtivos.

• Uma variável de entrada importante na negociação é a correlação entre os sinais. Nós fazemos uma série de experimentos de acordo com o coeficiente de correlação de 0 a 0.9. Os experimentos não levam em conta o custo da negociação (porque estamos interessados apenas no desempenho relativo) e a distribuição da taxa de retorno do portfólio anualizado, que é reequilibrado diariamente de acordo com a correlação, é basicamente a mesma.

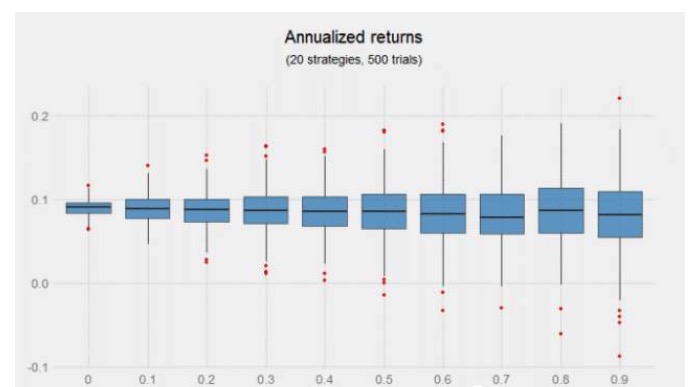
A combinação de sinais de baixa correlação não aumenta o rendimento, mas o gráfico acima sugere os benefícios que as estratégias adicionais podem trazer, especialmente quando essas estratégias não são correlacionadas. Na metade esquerda do gráfico, ou seja, o coeficiente de correlação de 0 a 0,4, a distribuição é mais estreita e o rendimento é positivo em quinhentos experimentos.

Os resultados ficam mais claros quando a proporção de Sharpe é usada para medir os ganhos ajustados ao risco. Uma combinação de 20 estratégias com uma proporção de Sharpe anual de 0,6 e um coeficiente de correlação de 0 produz um conjunto com uma proporção de Sharpe anual de 3 e uma combinação de 20 estratégias com uma proporção de Sharpe anual de 0,6 e um coeficiente de correlação de 0,9 produz um conjunto com uma proporção de Sharpe anual de 0,64, o primeiro com um rendimento 370% maior do que o último.

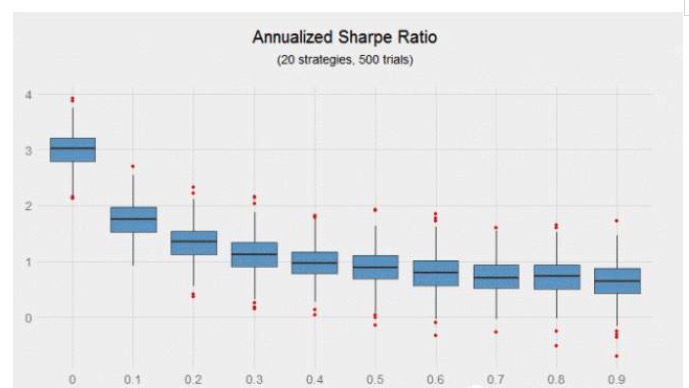
No gráfico acima, é notável que a taxa de Sharpe diminui rapidamente à medida que a relevância da estratégia aumenta. O coeficiente relevante aumenta de 0 para 0,2, e a taxa de Sharpe diminui 56%.

Mesmo com um Sharpe Ratio muito alto, esta estratégia combinada tem quase 50 mil sinais de negociação, e a diferença de Sharpe Ratio de uma combinação de correlação zero é surpreendente. Um investidor sortudo pode obter um Sharpe Ratio de 3.5 (que pode fazer uma pessoa milionária) e um investidor mal-sucedido com a mesma combinação pode obter apenas um Sharpe Ratio de 2.5. Mesmo com uma combinação de alto Sharpe Ratio, a sorte também desempenha um papel importante.

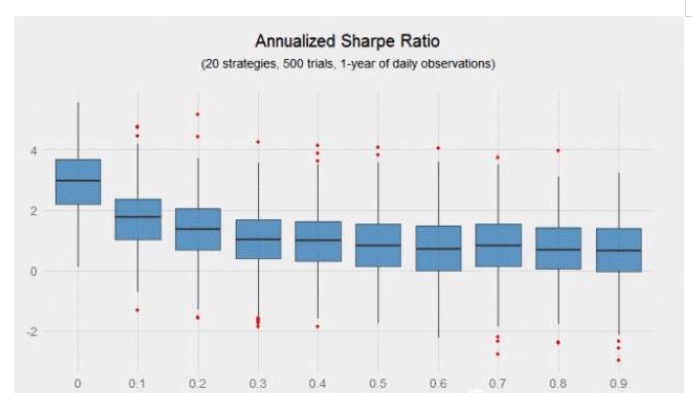
Obviamente, quanto mais amostras de observação, mais claras são as fronteiras. O que acontece se um investidor observa uma amostra de observação de apenas um ano, em vez de uma década? O gráfico abaixo mostra que, com o aumento da relevância, o diferencial da taxa de Sharpe cresce exponencialmente.

Se simularmos as 10000 estratégias individuais acima, qual é a proporção de p-valores abaixo de 5%? A resposta é perto de 48%, o que pode levar a maioria dos pesquisadores a desistir de estratégias diárias como esta (i.e., estratégias com uma taxa de Sharpe anual de 0.6). No entanto, se a correlação entre os sinais for baixa o suficiente, combinar esses sinais fracos juntos pode produzir milagres, e o fluxo de retorno do conjunto pode se tornar muito significativo.

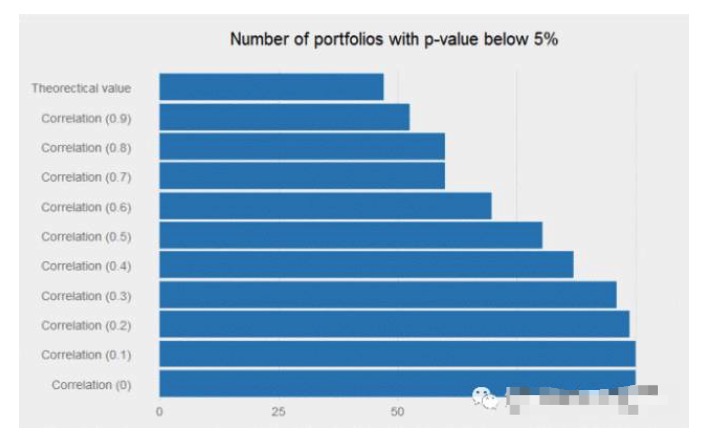
Uma estratégia de um Sharpe ratio anual de 0,6 pode ser descartada pelos pesquisadores por não ter qualquer atração nas negociações. Mas, se tiver a correlação correta (ou seja, baixa) entre os sinais existentes, pode aumentar muito o valor do portfólio.

Este artigo não abriu um novo campo, pois os benefícios do investimento diversificado são bem conhecidos na comunidade de investidores. Mas ele faz um lembrete de que você não precisa desistir da estratégia de uma taxa anual de Sharpe de 0,6. Talvez você possa adicioná-la ao seu portfólio de estratégias existentes, reduzindo a liquidez do portfólio e permitindo o uso de mais alavancagem para aumentar o retorno total.

Transcrição feita por: