Uma estratégia de negociação diurna que usa o regresso de igual valor entre SPY e IWM

Neste artigo, vamos escrever uma estratégia de negociação intradía. Ela usará o clássico conceito de negociação de pares de negociação de retorno de parâmetros de parâmetros. Neste exemplo, vamos usar dois fundos de índices abertos (ETFs), SPY e IWM, que são negociados no NYSE e tentam representar os índices dos mercados de ações dos EUA, respectivamente, o S&P 500 e o Russell 2000.

A estratégia é criar um diferencial de lucro fazendo mais de um ETF e fazendo o outro ETF vazio. O diferencial de lucro pode ser definido de várias maneiras, como por exemplo, usando a metodologia das sequências de tempo de coesão estatística. Nesse cenário, vamos calcular a taxa de hedge entre o SPY e o IWM através de regressão linear rolante. Isso nos permitirá criar um diferencial de lucro entre o SPY e o IWM, que é padronizado como um z-score.

O princípio básico da estratégia é que o SPY e o IWM representam aproximadamente a mesma situação do mercado, ou seja, o desempenho dos preços de ações de um grupo de grandes e pequenas empresas americanas. O pressuposto é que, se se aceitar a teoria do regresso do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmetro do parâmet

Estratégias

A estratégia é executada através dos seguintes passos:

Dados - 1 minuto de gráficos de k-string do SPY e do IWM, respectivamente, de abril de 2007 a fevereiro de 2014.

Processar - alinhar os dados corretamente e excluir k-strings que estão faltando um ao outro.

Diferença - o rácio de hedge entre os dois ETFs é calculado com uma regressão linear rotativa. Definido como o coeficiente de regresso β usando uma janela de retrocesso que move 1 linha k para a frente e recalcula o coeficiente de regresso. Assim, o rácio de hedge βi, a linha big K, é usado para recuar a linha k através do cálculo do ponto de travessia de bi-1-k para bi-1, para calcular o coeficiente de regresso k.

Z-Score - O valor do desvio padrão é calculado da maneira usual. Isso significa subtrair o valor médio do desvio padrão da amostra e subtrair o desvio padrão da amostra. A razão para fazer isso é para facilitar a compreensão dos parâmetros do limiar, pois o Z-Score é uma quantidade sem dimensão.

Negociação - quando o valor do z-score negativo cai para baixo do limite previsto (ou pós-optimizado), um sinal de fazer mais é gerado, enquanto o sinal de fazer nada é gerado ao contrário. Quando o valor absoluto do z-score cai para baixo do limite adicional, um sinal de equilíbrio é gerado. Para esta estratégia, eu (um pouco aleatoriamente) escolhi o z-score = 2 como limite de negociação aberto e o z-score = 1 como limite de negociação plana.

Talvez a melhor maneira de entender a política é implementá-la na prática. A seção a seguir apresenta em detalhes o código completo do Python para implementar essa política de retorno de igual valor (um único arquivo). Eu adicionei uma notação de código detalhada para ajudar você a entender melhor.

Implementação do Python

Como todos os tutoriais Python/pandas, o ambiente Python descrito neste tutorial deve ser configurado. Após a configuração, a primeira tarefa é importar a biblioteca Python necessária. Isso é necessário para usar matplotlib e pandas.

A versão específica da biblioteca que eu uso é a seguinte:

Python - 2.7.3 NumPy - 1.8.0 Pandas - 0.12.0 matplotlib - 1.1.0

Vamos continuar e importar estas bibliotecas:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

A seguinte função create_pairs_dataframe importa dois CSVs de k linhas internas que contêm dois símbolos. No nosso exemplo, isso seria SPY e IWM. Em seguida, ele cria um par de pares separados de pares de pares de dados, que usam os índices dos dois arquivos originais. Os seus tempos podem variar devido a transações e erros perdidos.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

O próximo passo é fazer uma regressão linear rotativa entre SPY e IWM. Neste cenário, IWM é o preditor (x), SPY é a resposta (y). Configurei uma janela de regressão padrão de 100 linhas k. Como mencionado acima, este é um parâmetro da política. Para que a política seja considerada robusta, idealmente queremos ver um relatório de retorno apresentando um estado de função convexa (x) ou outro desempenho de métrica de desempenho no período de regressão.

Depois de calcular o coeficiente de rotação β no modelo de regressão linear SPY-IWM, adicione-o ao par de DataFrame e remova as linhas vazias. Isso constrói o primeiro grupo de linhas K, que é igual a uma medida de corte de comprimento retrô. Então, criamos dois diferenciais de ETFs, unidades de SPY e unidades de -βi do IWM. Obviamente, isso não é real, porque estamos usando uma pequena quantidade de IWM, o que não é possível na implementação real.

Finalmente, criamos um z-score do diferencial, calculado subtraindo a média do diferencial e usando o padrão de diferencial padronizado. Note-se que existe um par de erros de visão de futuro bastante subtis aqui. Deixei-o intencionalmente no código porque queria enfatizar o quão fácil é cometer esses erros no estudo.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Em create_long_short_market_signals, os sinais de negociação são criados. Estes são calculados por um valor do z-score superior ao limiar. Quando o valor absoluto do z-score é menor ou igual a outro (menor) limiar, um sinal de equilíbrio é dado.

Para conseguir isso, é necessário estabelecer uma estratégia de negociação para cada linha k, quer seja um depósito aberto ou um depósito plano. Long_market e short_market são as duas variáveis definidas para rastrear posições de múltiplos e vazios. Infelizmente, é mais fácil de programar de forma iterativa em comparação com o método de quantificação e, portanto, é muito lento de calcular. Embora o gráfico de linha k de 1 minuto exija cerca de 700.000 pontos de dados por arquivo CSV, no meu desktop antigo ele ainda é relativamente rápido de calcular!

Para iterar um DataFrame panda (isto é, sem dúvida, uma operação incomum), é necessário usar o método iterrows, que fornece um gerador de iteração:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Neste estágio, atualizamos os pares para incluir sinais reais de múltiplos e vazios, o que nos permite determinar se precisamos ou não abrir um negócio. Agora precisamos criar um portfólio para rastrear o valor do mercado do posicionamento. A primeira tarefa é criar uma coluna de posições que combine sinais múltiplos e sinais vazios. Isso incluirá uma coluna de elementos a partir de ((1, 0, -1), onde 1 representa posições múltiplos, 0 representa nenhuma posição, e -1 representa posições vazias. sym1 e sym2 representam o valor do mercado das posições SPY e IWM no final de cada linha k.

Uma vez criado o valor de mercado do ETF, nós os combinamos para produzir o valor total de mercado no final de cada linha k. Depois, transformamos em valor de retorno através do método pct_change do objeto. A linha de código seguinte limpa as entradas erradas (NaN e inf elementos) e, finalmente, calcula a curva de direitos completa.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

A função principal os combina. O arquivo CSV no dia está localizado no caminho datadir. Certifique-se de modificar o código abaixo para apontar para o seu diretório específico.

Para determinar a sensibilidade da estratégia aos ciclos de lookback, é necessário calcular uma série de indicadores de desempenho do lookback. Escolhi a percentagem de retorno total final do portfólio como indicador de desempenho e o intervalo de lookback [50,200], com um aumento de 10. Você pode ver no código abaixo que a função anterior está incluída no ciclo for dentro desse intervalo, enquanto outros limites permanecem inalterados. A última tarefa é criar um gráfico de linha de lookbacks versus retornos usando o matplotlib:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

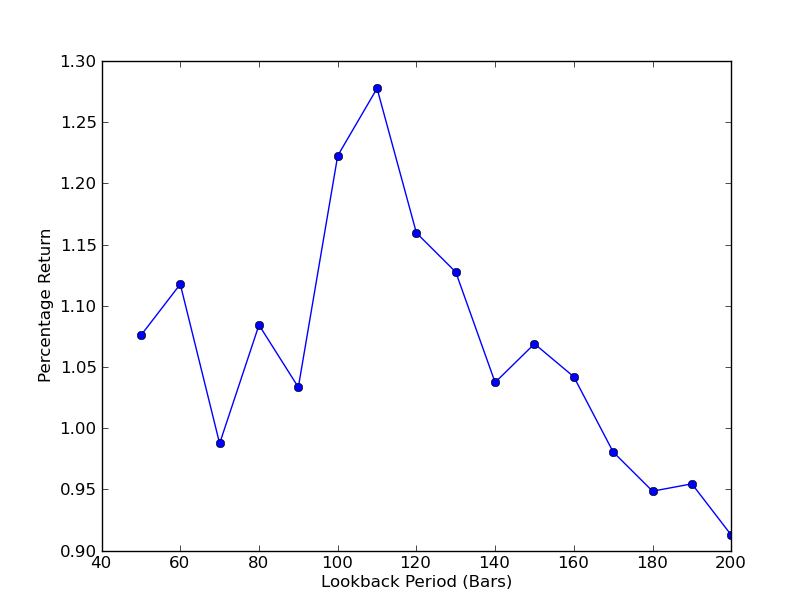
Agora, podemos ver um gráfico de lookbacks e retornos. Note que lookback tem um valor máximo de lookbacks global, igual a 110 k-strings. Se vemos que lookbacks não têm relação com retornos, é porque:

Análise de sensibilidade do período de hedge de regressão linear do SPY-IWM em relação ao lookback

Sem curvas de lucro inclinadas para cima, qualquer artigo de retrospectiva é incompleto! Portanto, se você deseja traçar uma curva de retorno de lucro acumulado e tempo, use o seguinte código. Ele desenhará o portfólio final gerado a partir do estudo dos parâmetros do lookback. Portanto, é necessário selecionar o lookback com base no gráfico que você deseja visualizar.

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

O seguinte gráfico da curva de direitos e benefícios tem um lookback de 100 dias:

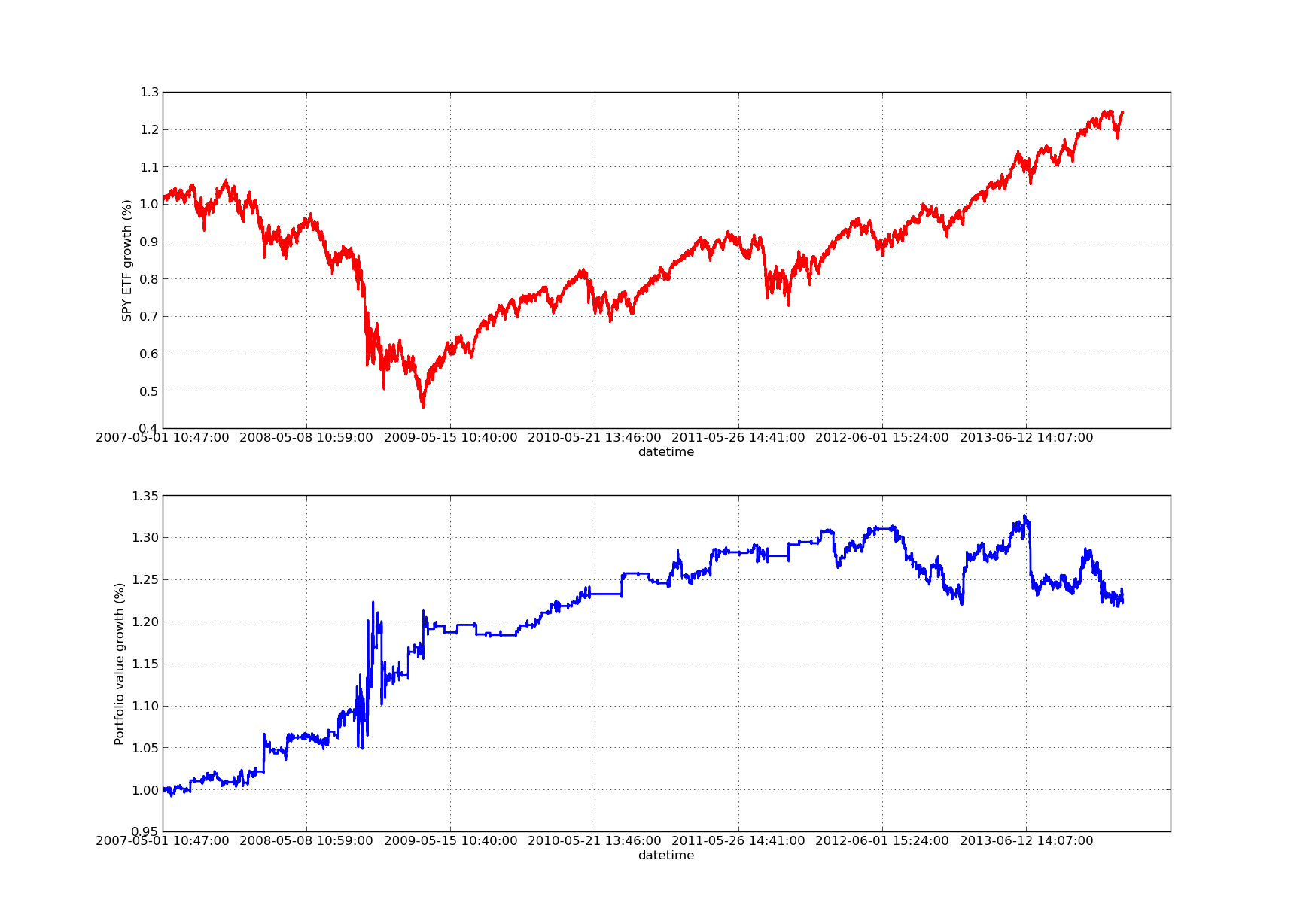
Análise de sensibilidade do período de hedge de regressão linear do SPY-IWM em relação ao lookback

Observe que o SPY em 2009 teve um grande decréscimo durante a crise financeira. A estratégia também está em um período de turbulência nesta fase. Observe também que o desempenho do ano passado piorou devido à natureza fortemente tendencial do SPY durante este período, refletindo o índice S&P 500.

Observe que, ao calcular o desfalque do z-score, ainda precisamos considerar o desfalque da visão de futuro. Além disso, todos esses cálculos foram feitos sem custos de transação. Uma vez que esses fatores são considerados, a estratégia certamente vai se apresentar muito mal.

Em artigos posteriores, criaremos um backtester mais complexo, impulsionado por eventos, que levará em consideração esses fatores e nos dará mais confiança na curva de capital e nos indicadores de desempenho.