No artigo anterior (https://www.fmz.com/digest-topic/4187), apresentamos estratégias de negociação de pares e demonstramos como usar dados e análise matemática para criar e automatizar estratégias de negociação.

A estratégia de ações balanceadas long-short é uma extensão natural da estratégia de pair trading aplicável a uma cesta de alvos de negociação. É particularmente adequado para negociar mercados com muitas variedades e inter-relações, como o mercado de moeda digital e o mercado futuro de commodities.

Princípios básicos

A estratégia de ações balanceadas long-short consiste em operar comprado e vendido em uma cesta de alvos de negociação ao mesmo tempo. Assim como o pair trading, determine quais alvos de investimento são baratos e quais são caros. A diferença é que a estratégia de ações balanceadas long-short classificará todos os alvos de investimento em um pool de seleção de ações para determinar quais alvos de investimento são relativamente baratos. Ou caros. Em seguida, ele entrará em posição comprada nos n principais investimentos com base na classificação e vendida nos n últimos investimentos com um valor igual (valor total das posições compradas = valor total das posições vendidas).

Lembra quando dissemos anteriormente que a negociação de pares é uma estratégia neutra de mercado? O mesmo vale para uma estratégia de ações balanceadas long-short, pois quantidades iguais de posições longas e curtas garantem que a estratégia permanecerá neutra em relação ao mercado (não afetada pelas flutuações do mercado). A estratégia também é estatisticamente robusta; ao classificar investimentos e assumir múltiplas posições, você pode expor seu modelo de classificação a múltiplas exposições, em vez de apenas uma exposição única ao risco. A única coisa em que você está apostando é na qualidade do seu esquema de classificação.

O que é um esquema de classificação?

Um esquema de classificação é um modelo que atribui uma prioridade a cada meta de investimento com base em seu desempenho esperado. Os fatores podem ser fatores de valor, indicadores técnicos, modelos de precificação ou uma combinação de todos os itens acima. Por exemplo, você pode usar a métrica de momentum para classificar uma lista de investimentos que seguem tendências: espera-se que os investimentos com o maior momentum continuem a ter um bom desempenho e recebam as classificações mais altas; os investimentos com o menor momentum teriam o pior desempenho e têm os menores retornos.

O sucesso dessa estratégia depende quase inteiramente do esquema de classificação utilizado, ou seja, seu esquema de classificação é capaz de separar investimentos de alto desempenho de investimentos de baixo desempenho, obtendo melhor os retornos da estratégia de investimento de longo prazo-curto prazo. Portanto, é muito importante desenvolver um esquema de classificação.

Como formular um plano de classificação?

Uma vez que tenhamos um esquema de classificação em vigor, obviamente queremos lucrar com ele. Fazemos isso investindo a mesma quantia de dinheiro para operar comprado nos investimentos mais bem classificados e vendido nos investimentos menos bem classificados. Isso garante que a estratégia só ganhará dinheiro na proporção da qualidade de suas classificações e será “neutra em relação ao mercado”.

Suponha que você esteja classificando todos os investimentos m, tenha n dólares para investir e queira manter um total de 2p (onde m>2p) posições. Se espera-se que o investimento com classificação 1 tenha o pior desempenho, então espera-se que o investimento com classificação m tenha o melhor desempenho:

• Você organiza as metas de investimento da seguinte forma: 1, …, p e metas de investimento curtas de 2/2p em USD

• Você organiza as metas de investimento como: m-p,……,m, e opera longo em n/2p dólares de metas de investimento

Perceber:Como o preço-alvo devido a saltos de preço nem sempre dividirá n/2p uniformemente, e alguns alvos devem ser comprados em números inteiros, haverá alguns algoritmos inexatos, e o algoritmo deve ser o mais próximo possível desse número. Para a estratégia executada com n = 100000 e p = 500, vemos:

n/2p = ¹⁰⁰⁰⁰⁰⁄₁₀₀₀ = 100

Isso pode causar grandes problemas para preços com frações maiores que 100 (como mercados futuros de commodities), porque você não pode abrir posições com preços fracionários (esse problema não existe no mercado de criptomoedas). Nós mitigamos isso reduzindo negociações de preços fracionários ou aumentando o capital.

Vejamos um exemplo hipotético.

• Construindo nosso ambiente de pesquisa na Plataforma Quantitativa Inventor

Primeiro de tudo, para trabalhar sem problemas, precisamos construir nosso ambiente de pesquisa. Neste artigo, usamos a Inventor Quantitative Platform (FMZ.COM) para construir o ambiente de pesquisa, principalmente para que possamos usar a API conveniente e rápida interface e encapsulamento desta plataforma posteriormente. Sistema Docker completo.

No nome oficial da Inventor Quantitative Platform, esse sistema Docker é chamado de sistema host.

Para obter mais informações sobre como implantar hosts e robôs, consulte meu artigo anterior: https://www.fmz.com/bbs-topic/4140

Os leitores que desejam adquirir seu próprio host de implantação de servidor de computação em nuvem podem consultar este artigo: https://www.fmz.com/bbs-topic/2848

Após a implantação bem-sucedida do serviço de computação em nuvem e do sistema host, instalaremos a ferramenta Python mais poderosa: Anaconda

Para obter todos os ambientes de programa relevantes necessários para este artigo (bibliotecas dependentes, gerenciamento de versões, etc.), a maneira mais fácil é usar o Anaconda. É um ecossistema de ciência de dados Python empacotado e um gerenciador de dependências.

Para o método de instalação do Anaconda, consulte o guia oficial do Anaconda: https://www.anaconda.com/distribution/

Este artigo também usará numpy e pandas, duas bibliotecas muito populares e importantes na computação científica Python.

Para o trabalho básico acima, você também pode consultar meu artigo anterior, que apresenta como configurar o ambiente Anaconda e as duas bibliotecas numpy e pandas. Para detalhes, consulte: https://www.fmz.com/digest- tópico/4169

Geramos investimentos e fatores aleatórios e os classificamos. Vamos supor que nossos retornos futuros realmente dependam desses valores de fatores.

import numpy as np
import statsmodels.api as sm
import scipy.stats as stats
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
## PROBLEM SETUP ##
# Generate stocks and a random factor value for them
stock_names = ['stock ' + str(x) for x in range(10000)]
current_factor_values = np.random.normal(0, 1, 10000)
# Generate future returns for these are dependent on our factor values
future_returns = current_factor_values + np.random.normal(0, 1, 10000)
# Put both the factor values and returns into one dataframe
data = pd.DataFrame(index = stock_names, columns=['Factor Value','Returns'])
data['Factor Value'] = current_factor_values
data['Returns'] = future_returns
# Take a look
data.head(10)

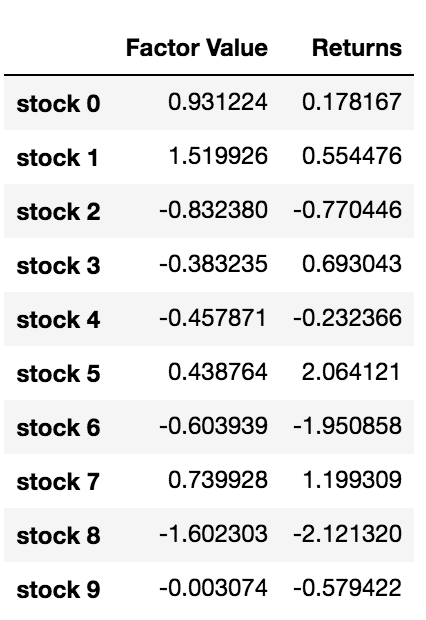
Agora que temos valores de fatores e retornos, podemos ver o que acontece se classificarmos os investimentos com base nos valores de fatores e então abrirmos posições longas e curtas.

# Rank stocks
ranked_data = data.sort_values('Factor Value')
# Compute the returns of each basket with a basket size 500, so total (10000/500) baskets
number_of_baskets = int(10000/500)
basket_returns = np.zeros(number_of_baskets)
for i in range(number_of_baskets):
    start = i * 500
    end = i * 500 + 500 
    basket_returns[i] = ranked_data[start:end]['Returns'].mean()
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

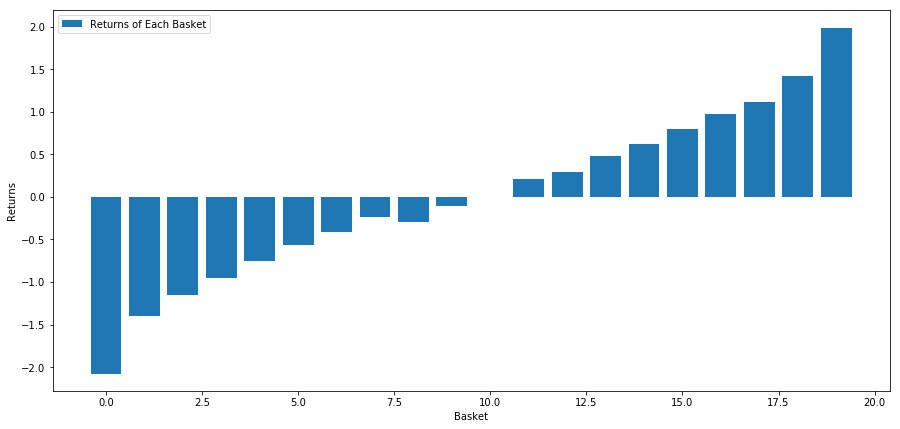
Nossa estratégia é operar comprado no primeiro investimento classificado em uma cesta de alvos de investimento e vendido no décimo alvo de investimento classificado. As recompensas desta estratégia são:

basket_returns[number_of_baskets-1] - basket_returns[0]

O resultado é: 4.172

Aposte em nosso modelo de classificação para separar investimentos de alto desempenho dos de baixo desempenho.

No restante deste artigo, discutiremos como avaliar esquemas de classificação. O benefício de ganhar dinheiro com arbitragem baseada em classificação é que ela não é afetada pela desordem do mercado, mas pode tirar vantagem dela.

Vamos considerar um exemplo do mundo real.

Carregamos dados de 32 ações de diferentes setores no S&P 500 e tentamos classificá-las.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2010/01/01'
endDateStr = '2017/12/31'
cachedFolderName = '/Users/chandinijain/Auquan/yahooData/'
dataSetId = 'testLongShortTrading'
instrumentIds = ['ABT','AKS','AMGN','AMD','AXP','BK','BSX',
                'CMCSA','CVS','DIS','EA','EOG','GLW','HAL',
                'HD','LOW','KO','LLY','MCD','MET','NEM',
                'PEP','PG','M','SWN','T','TGT',
                'TWX','TXN','USB','VZ','WFC']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
price = 'adjClose'

Vamos usar o indicador de momentum normalizado ao longo de um período de um mês como base para classificação

## Define normalized momentum
def momentum(dataDf, period):
    return dataDf.sub(dataDf.shift(period), fill_value=0) / dataDf.iloc[-1]
## Load relevant prices in a dataframe
data = ds.getBookDataByFeature()[‘Adj Close’]
#Let's load momentum score and returns into separate dataframes
index = data.index
mscores = pd.DataFrame(index=index,columns=assetList)
mscores = momentum(data, 30)
returns = pd.DataFrame(index=index,columns=assetList)
day = 30

Agora analisaremos o comportamento das nossas ações e veremos como elas se saem no mercado dentro dos fatores de classificação que escolhemos.

Analisar os dados

Comportamento do estoque

Vamos dar uma olhada no desempenho da nossa cesta selecionada de ações em nosso modelo de classificação. Para fazer isso, vamos calcular os retornos futuros de uma semana para todas as ações. Podemos então analisar a correlação do retorno futuro de 1 semana de cada ação com o momentum anterior de 30 dias. Ações que mostram correlação positiva seguem tendências, e ações que mostram correlação negativa revertem à média.

# Calculate Forward returns
forward_return_day = 5
returns = data.shift(-forward_return_day)/data -1
returns.dropna(inplace = True)
# Calculate correlations between momentum and returns
correlations = pd.DataFrame(index = returns.columns, columns = [‘Scores’, ‘pvalues’])
mscores = mscores[mscores.index.isin(returns.index)]
for i in correlations.index:
    score, pvalue = stats.spearmanr(mscores[i], returns[i])
    correlations[‘pvalues’].loc[i] = pvalue
    correlations[‘Scores’].loc[i] = score
correlations.dropna(inplace = True)
correlations.sort_values(‘Scores’, inplace=True)
l = correlations.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correlations[‘Scores’])
plt.xlabel(‘Stocks’)
plt.xlim((1, l+1))
plt.xticks(range(1,1+l), correlations.index)
plt.legend([‘Correlation over All Data’])
plt.ylabel(‘Correlation between %s day Momentum Scores and %s-day forward returns by Stock’%(day,forward_return_day));
plt.show()

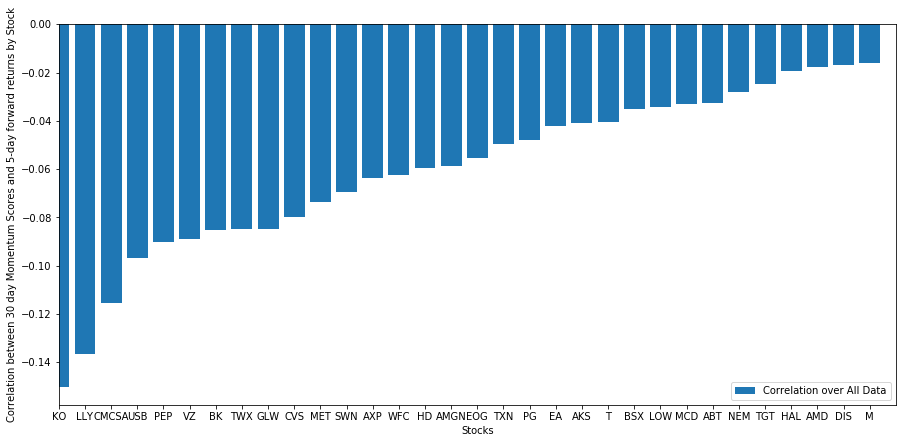
Todas as nossas ações significam reversão em algum grau! (Aparentemente, nosso universo escolhido funciona dessa maneira.) Isso nos diz que se uma ação tem uma classificação alta na análise de momentum, devemos esperar que ela tenha um desempenho inferior na semana que vem.

Correlação entre classificação de pontuação de momentum e retornos

Em seguida, precisamos olhar para a correlação entre nossa pontuação de classificação e os retornos forward gerais do mercado, ou seja, a relação entre a previsão de retornos esperados e nossos fatores de classificação. Níveis de correlação mais altos podem prever retornos relativos mais pobres, ou vice-versa?

Para fazer isso, calculamos a correlação diária entre o momentum de 30 dias e os retornos futuros de 1 semana para todas as ações.

correl_scores = pd.DataFrame(index = returns.index.intersection(mscores.index), columns = [‘Scores’, ‘pvalues’])
for i in correl_scores.index:
    score, pvalue = stats.spearmanr(mscores.loc[i], returns.loc[i])
    correl_scores[‘pvalues’].loc[i] = pvalue
    correl_scores[‘Scores’].loc[i] = score
correl_scores.dropna(inplace = True)
l = correl_scores.index.size
plt.figure(figsize=(15,7))
plt.bar(range(1,1+l),correl_scores[‘Scores’])
plt.hlines(np.mean(correl_scores[‘Scores’]), 1,l+1, colors=’r’, linestyles=’dashed’)
plt.xlabel(‘Day’)
plt.xlim((1, l+1))
plt.legend([‘Mean Correlation over All Data’, ‘Daily Rank Correlation’])
plt.ylabel(‘Rank correlation between %s day Momentum Scores and %s-day forward returns’%(day,forward_return_day));
plt.show()

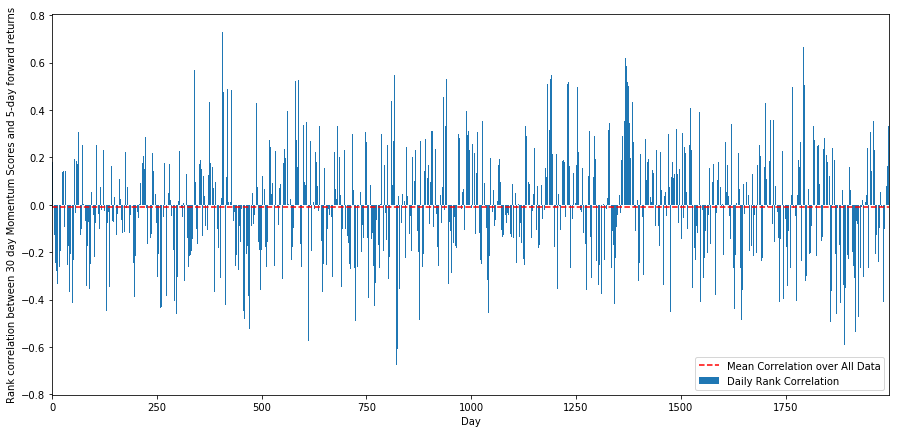
A correlação diária é bastante ruidosa, mas muito leve (o que é esperado, já que dissemos que todas as ações significarão reversão). Também analisamos a correlação média mensal dos retornos futuros de 1 mês.

monthly_mean_correl =correl_scores['Scores'].astype(float).resample('M').mean()
plt.figure(figsize=(15,7))
plt.bar(range(1,len(monthly_mean_correl)+1), monthly_mean_correl)
plt.hlines(np.mean(monthly_mean_correl), 1,len(monthly_mean_correl)+1, colors='r', linestyles='dashed')
plt.xlabel('Month')
plt.xlim((1, len(monthly_mean_correl)+1))
plt.legend(['Mean Correlation over All Data', 'Monthly Rank Correlation'])
plt.ylabel('Rank correlation between %s day Momentum Scores and %s-day forward returns'%(day,forward_return_day));
plt.show()

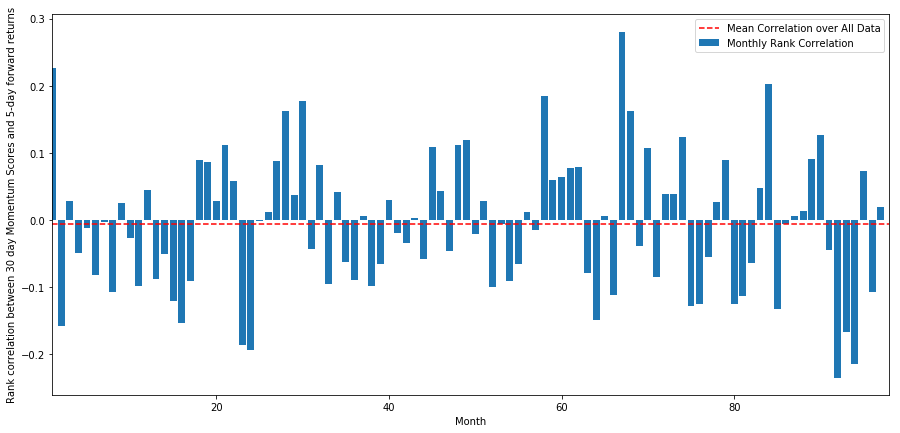
Podemos ver que a correlação média é novamente ligeiramente negativa, mas também varia muito de mês para mês.

Retornos médios da cesta de ações

Calculamos os retornos para uma cesta de ações retiradas da nossa classificação. Se classificarmos todas as ações e depois as dividirmos em n grupos, qual será o retorno médio de cada grupo?

O primeiro passo é criar uma função que fornecerá o retorno médio e o fator de classificação para cada cesta fornecida a cada mês.

def compute_basket_returns(factor, forward_returns, number_of_baskets, index):
data = pd.concat([factor.loc[index],forward_returns.loc[index]], axis=1)
    # Rank the equities on the factor values
    data.columns = ['Factor Value', 'Forward Returns']
    data.sort_values('Factor Value', inplace=True)
    # How many equities per basket
    equities_per_basket = np.floor(len(data.index) / number_of_baskets)
basket_returns = np.zeros(number_of_baskets)
# Compute the returns of each basket
    for i in range(number_of_baskets):
        start = i * equities_per_basket
        if i == number_of_baskets - 1:
            # Handle having a few extra in the last basket when our number of equities doesn't divide well
            end = len(data.index) - 1
        else:
            end = i * equities_per_basket + equities_per_basket
        # Actually compute the mean returns for each basket
        #s = data.index.iloc[start]
        #e = data.index.iloc[end]
        basket_returns[i] = data.iloc[int(start):int(end)]['Forward Returns'].mean()
        
    return basket_returns

Calculamos o retorno médio de cada cesta ao classificar as ações com base nessa pontuação. Isso deve nos dar uma boa ideia do relacionamento deles ao longo do tempo.

number_of_baskets = 8
mean_basket_returns = np.zeros(number_of_baskets)
resampled_scores = mscores.astype(float).resample('2D').last()
resampled_prices = data.astype(float).resample('2D').last()
resampled_scores.dropna(inplace=True)
resampled_prices.dropna(inplace=True)
forward_returns = resampled_prices.shift(-1)/resampled_prices -1
forward_returns.dropna(inplace = True)
for m in forward_returns.index.intersection(resampled_scores.index):
    basket_returns = compute_basket_returns(resampled_scores, forward_returns, number_of_baskets, m)
    mean_basket_returns += basket_returns
mean_basket_returns /= l    
print(mean_basket_returns)
# Plot the returns of each basket
plt.figure(figsize=(15,7))
plt.bar(range(number_of_baskets), mean_basket_returns)
plt.ylabel('Returns')
plt.xlabel('Basket')
plt.legend(['Returns of Each Basket'])
plt.show()

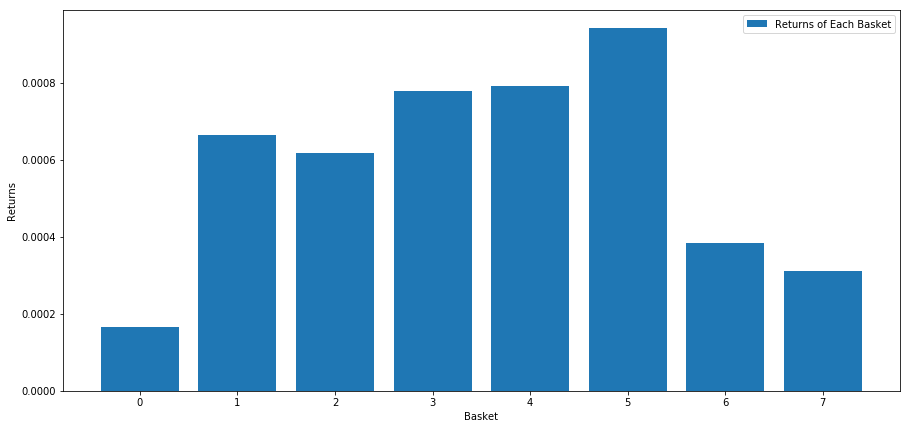
Parece que conseguimos separar os de alto desempenho dos de baixo desempenho.

Consistência de propagação (base)

Claro, esses são apenas relacionamentos comuns. Para entender o quão consistente é o relacionamento e se estamos dispostos a fazer um acordo, devemos mudar nossa abordagem e atitude em relação a ele ao longo do tempo. A seguir, veremos seus spreads mensais (base) dos dois anos anteriores. Podemos ver mais mudanças e realizar análises mais aprofundadas para determinar se essa pontuação de momentum é negociável.

total_months = mscores.resample('M').last().index
months_to_plot = 24
monthly_index = total_months[:months_to_plot+1]
mean_basket_returns = np.zeros(number_of_baskets)
strategy_returns = pd.Series(index = monthly_index)
f, axarr = plt.subplots(1+int(monthly_index.size/6), 6,figsize=(18, 15))
for month in range(1, monthly_index.size):
    temp_returns = forward_returns.loc[monthly_index[month-1]:monthly_index[month]]
    temp_scores = resampled_scores.loc[monthly_index[month-1]:monthly_index[month]]
    for m in temp_returns.index.intersection(temp_scores.index):
        basket_returns = compute_basket_returns(temp_scores, temp_returns, number_of_baskets, m)
        mean_basket_returns += basket_returns
    
    strategy_returns[monthly_index[month-1]] = mean_basket_returns[ number_of_baskets-1] - mean_basket_returns[0]
    
    mean_basket_returns /= temp_returns.index.intersection(temp_scores.index).size
    
    r = int(np.floor((month-1) / 6))
    c = (month-1) % 6
    axarr[r, c].bar(range(number_of_baskets), mean_basket_returns)
    axarr[r, c].xaxis.set_visible(False)
    axarr[r, c].set_title('Month ' + str(month))
plt.show()

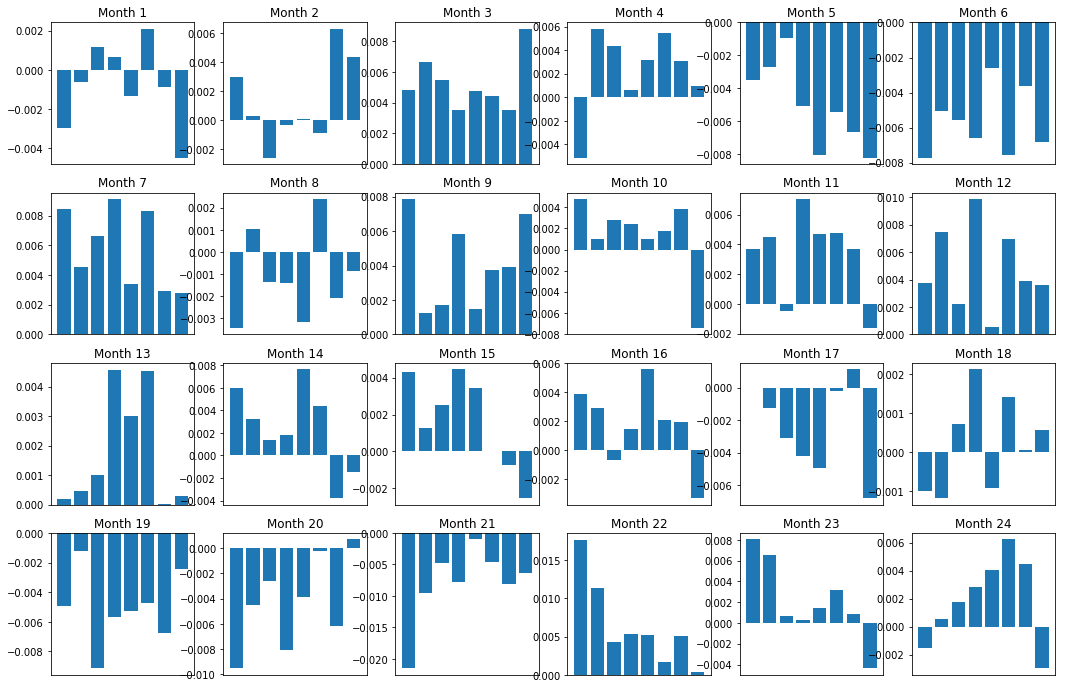
plt.figure(figsize=(15,7))
plt.plot(strategy_returns)
plt.ylabel(‘Returns’)
plt.xlabel(‘Month’)
plt.plot(strategy_returns.cumsum())
plt.legend([‘Monthly Strategy Returns’,’Cumulative Strategy Returns’])
plt.show()

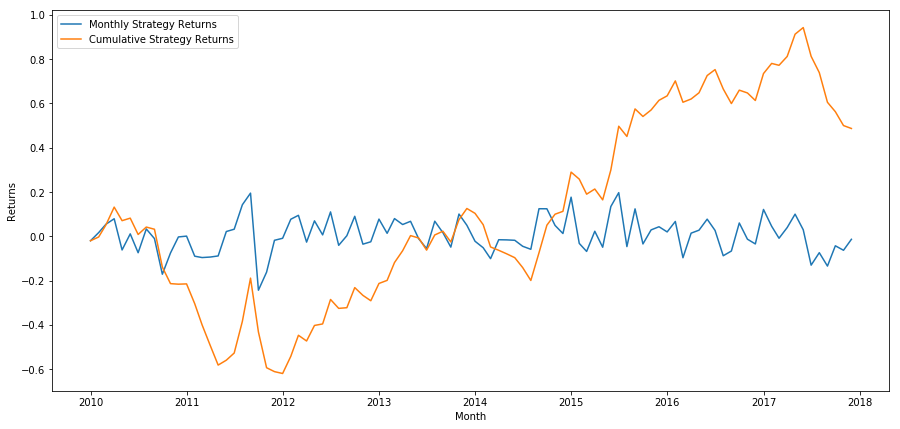
Por fim, vejamos os retornos se estivéssemos comprados na última cesta e vendidos na primeira cesta a cada mês (assumindo alocação igual de capital para cada título)

total_return = strategy_returns.sum()
ann_return = 100*((1 + total_return)**(12.0 /float(strategy_returns.index.size))-1)
print('Annual Returns: %.2f%%'%ann_return)

Retorno anual: 5,03%

Vemos que temos um esquema de classificação muito fraco que distingue apenas modestamente ações de alto desempenho de ações de baixo desempenho. Além disso, não há consistência nesse esquema de classificação e ele varia muito de mês para mês.

Encontrando o esquema de classificação correto

Para implementar uma estratégia de ações balanceadas long-short, você só precisa determinar o esquema de classificação. Tudo depois disso é mecânico. Depois de ter uma estratégia de ações balanceadas de longo e curto prazo, você pode alternar diferentes fatores de classificação sem alterar muito mais. Essa é uma maneira muito conveniente de iterar rapidamente suas ideias sem ter que se preocupar em ajustar o código inteiro toda vez.

O esquema de classificação também pode vir de quase qualquer modelo. Não precisa ser um modelo de fator baseado em valor, pode ser uma técnica de aprendizado de máquina que prevê retornos com um mês de antecedência e os classifica com base nisso.

Seleção e avaliação de esquemas de classificação

O esquema de classificação é a vantagem da estratégia de ações equilibradas long-short e também é o componente mais importante. Escolher um bom esquema de classificação é um projeto sistemático e não há respostas simples.

Um bom ponto de partida é escolher tecnologias conhecidas e ver se você pode modificá-las ligeiramente para obter retornos maiores. Discutiremos alguns pontos de partida aqui:

• Clonar e ajustar: Escolha algo que seja frequentemente discutido e veja se você pode modificá-lo ligeiramente a seu favor. Normalmente, os fatores públicos não terão mais sinais de negociação porque foram totalmente arbitrados fora do mercado. No entanto, às vezes eles podem orientá-lo na direção certa.

• Modelo de preços: Qualquer modelo que preveja retornos futuros pode ser um fator e tem o potencial de ser usado para classificar sua cesta de alvos de negociação. Você pode pegar qualquer modelo de precificação complexo e convertê-lo em um esquema de classificação.

• Fatores baseados em preço (indicadores técnicos): Fatores baseados em preço, como os que discutimos hoje, pegam informações sobre o preço histórico de cada ação e as usam para gerar um valor de fator. Exemplos podem ser indicadores de média móvel, indicadores de momentum ou indicadores de volatilidade.

• Regressão e Momentum: Vale ressaltar que alguns fatores acreditam que, uma vez que os preços se movem em uma direção, eles continuarão assim. Alguns fatores são exatamente o oposto. Ambos são modelos válidos em diferentes períodos de tempo e ativos, e é importante estudar se o comportamento subjacente é baseado em momentum ou regressão.

• Fatores Fundamentais (Baseados em Valor):Isso usa uma combinação de valores fundamentais como PE, dividendos etc. O valor fundamental contém informações relacionadas a fatos do mundo real sobre uma empresa e, portanto, pode ser mais poderoso que o preço de muitas maneiras.

Em última análise, desenvolver preditores é uma corrida armamentista em que você tenta ficar um passo à frente. Os fatores são arbitrados fora do mercado e têm um tempo de vida útil, então você deve trabalhar continuamente para determinar quanta deterioração seus fatores sofreram e quais novos fatores podem ser usados ​​para substituí-los.

Outras considerações

• Frequência de reequilíbrio

Cada sistema de classificação prevê retornos em um período de tempo ligeiramente diferente. A reversão média baseada em preço pode ser preditiva ao longo de alguns dias, enquanto os modelos de fatores baseados em valor podem ser preditivos ao longo de alguns meses. É muito importante determinar o horizonte de tempo que o modelo deve prever e validá-lo estatisticamente antes de executar a estratégia. Você certamente não quer se ajustar demais ao tentar otimizar sua frequência de rebalanceamento; você inevitavelmente encontrará uma que supera aleatoriamente as outras. Depois de determinar o horizonte de tempo que seu esquema de classificação prevê, tente rebalancear aproximadamente nessa frequência para aproveite ao máximo seu modelo.

• Capacidade de capital e custos de transação

Cada estratégia tem um requisito de capital mínimo e máximo, com o limite mínimo geralmente determinado pelos custos de transação.

Negociar muitas ações resultará em altos custos de transação. Supondo que você queira comprar 1.000 ações, cada rebalanceamento incorrerá em custos de vários milhares de dólares. Sua base de capital deve ser alta o suficiente para que os custos de transação representem uma pequena fração dos retornos gerados por sua estratégia. Por exemplo, se seu capital for de US\( 100.000 e sua estratégia render 1% (US\) 1.000) ao mês, todo esse retorno será consumido pelos custos de transação. Você precisaria de milhões de dólares de capital para executar essa estratégia e lucrar com mais de 1.000 ações.

O limite mínimo de ativos depende principalmente do número de ações negociadas. No entanto, a capacidade máxima também é muito alta, e as estratégias de ações balanceadas long-short são capazes de negociar centenas de milhões de dólares sem perder sua vantagem. Isso é verdade porque a estratégia é rebalanceada relativamente raramente. O valor total do ativo dividido pelo número de ações negociadas dará um valor em dólar muito baixo por ação, e você não precisa se preocupar com seu volume de negociação movendo o mercado. Digamos que você negocie 1.000 ações, isso dá US\( 100.000.000. Se você reequilibrasse todo o seu portfólio todo mês, estaria negociando apenas US\) 100.000 por mês por ação, o que não é suficiente para representar uma fatia significativa do mercado para a maioria dos títulos.