Бактестирование стратегии реверсионных пар внутридневного значения между SPY и IWM

В этой статье мы рассмотрим нашу первую стратегию внутридневного трейдинга. Она будет использовать классическую торговую идею, торговые пары. В данном случае мы будем использовать два биржевых фондов (ETF), SPY и IWM, которые торгуются на Нью-Йоркской фондовой бирже (NYSE) и пытаются представлять индексы фондового рынка США, S&P500 и Russell 2000, соответственно.

Стратегия в целом создает спред между парой ETF, затягивая один и коротко обменивая сумму другого. Соотношение длинного к короткому может быть определено многими способами, такими как использование методов статистических коинтегрирующих временных рядов. В этом сценарии мы будем рассчитывать соотношение хеджирования между SPY и IWM с помощью линейной регрессии. Это позволит нам создать спред между SPY и IWM, который нормализуется до z-соотношения. Торговые сигналы будут генерироваться, когда z-соотношение превышает определенные пороги, полагая, что спред вернется к среднему.

Основанием для этой стратегии является то, что SPY и IWM примерно характеризуют одну и ту же ситуацию, экономику группы крупнокапитализированных и мелкокапитализированных корпораций США. Предпосылка заключается в том, что если взять спред цен, то он должен быть средне-обратным, поскольку, хотя локальные (в времени) события могут влиять либо на индексы S&P500, либо на индексы Russell 2000 отдельно (например, различия между мелкой капитализацией и крупной капитализацией, даты ребалансирования или блок-трейды), долгосрочные ценовые ряды этих двух, вероятно, будут совместно интегрированы.

Стратегия

Стратегия реализуется в следующих этапах:

1. Данные - 1-минутные панели SPY и IWM получены с апреля 2007 года по февраль 2014 года.
2. Обработка - данные правильно выравниваются и отсутствующие строки взаимно отбрасываются.
3. Распространение - соотношение хеджирования между двумя ETF рассчитывается с помощью линейной регрессии. Это определяется как коэффициент регрессии β с использованием окна обратного просмотра, которое смещается вперед на 1 бар и пересчитывает коэффициенты регрессии. Таким образом, соотношение хеджирования βi для бар би рассчитывается по точкам bi−1−k до bi−1 для обратного просмотра k бар.
4. Z-Score - стандартный балл спреда рассчитывается обычным способом. Это означает вычитание среднего значения (выборки) спреда и деление на стандартное отклонение (выборки) спреда. Разум этого заключается в том, чтобы сделать пороговые параметры более простыми для интерпретации, поскольку z-score является безмерной величиной. Я намеренно ввел в расчеты предвзятость взгляда, чтобы показать, насколько она может быть тонкой. Попробуйте и следите за ней!
5. Торговля - длинные сигналы генерируются, когда отрицательный z-оценка опускается ниже заранее определенного (или пост-оптимизированного) порога, в то время как короткие сигналы являются обратным. Выходные сигналы генерируются, когда абсолютный z-оценка опускается ниже дополнительного порога. Для этой стратегии я (несколько произвольно) выбрал абсолютный порог входа z z = 2 и порог выхода z z z = 1. Предполагая среднее обращение поведения в спреде, это, надеюсь, захватит эту связь и обеспечит положительную производительность.

Возможно, лучший способ глубоко понять стратегию - это фактически ее реализовать. Следующий раздел описывает полный код Python (единый файл) для реализации этой стратегии обратного отсчета среднего. Я щедро прокомментировал код, чтобы помочь понять.

Использование Python

Как и во всех учебных пособиях Python/pandas, необходимо установить исследовательскую среду Python, как описано в этом учебном пособии. После установки первой задачей является импорт необходимых библиотек Python. Для этого требуется backtest matplotlib и pandas.

Конкретные версии библиотек, которые я использую, следующие:

• Python - 2.7.3
• NumPy - 1.8.0
• Панды - 0.12.0
• Matplotlib - 1.1.0 Давайте продолжим и импортируем библиотеки:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Следующая функция create_pairs_dataframe импортирует два файла CSV, содержащих внутридневные полоски двух символов. В нашем случае это будут SPY и IWM. Затем он создает отдельные пары данных, которые используют индексы обоих оригинальных файлов. Поскольку их временные знаки, вероятно, будут отличаться из-за пропущенных сделок и ошибок, это гарантирует, что у нас будут совпадающие данные. Это одно из основных преимуществ использования библиотеки анализа данных, такой как панды.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Следующим шагом является выполнение линейной регрессии между SPY и IWM. В этом случае IWM является предсказателем (x) и SPY является ответом (y). Я установил окно обратного просмотра по умолчанию в 100 бар. Как обсуждалось выше, это параметр стратегии. Чтобы стратегия считалась надежной, мы в идеале хотим видеть профиль возврата (или другую меру производительности) как выпуклую функцию обратного периода. Таким образом, на более позднем этапе кода мы проведем анализ чувствительности, изменяя период обратного просмотра в диапазоне.

После того, как коэффициент бета-коэффициента будет рассчитан в модели линейной регрессии для SPY-IWM, мы добавим его к парам DataFrame и упустим пустые строки. Это составляет первый набор строк, равных размеру обратного взгляда в качестве меры обрезания. Затем мы создаем распространение двух ETF как единицы SPY и −βi единиц IWM. Очевидно, что это не реалистичная ситуация, поскольку мы принимаем дробные количества IWM, что невозможно в реальной реализации.

Наконец, мы создаем z-балл распространения, который рассчитывается путем вычитания среднего значения распространения и нормализации стандартным отклонением распространения. Обратите внимание, что здесь происходит довольно тонкое уклонение. Я намеренно оставил его в коде, так как хотел подчеркнуть, насколько легко совершить такую ошибку в исследовании. Среднее и стандартное отклонение рассчитываются для всего временного ряда распространения. Если это отражает истинную историческую точность, то эта информация не была бы доступна, поскольку она косвенно использует будущую информацию. Таким образом, мы должны использовать колеблющуюся среднюю величину и stdev для расчета z-балла.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

В create_long_short_market_signals создаются торговые сигналы. Они рассчитываются путем длинного распространения, когда z-соотношение отрицательно превышает отрицательный z-соотношение, и короткого распространения, когда z-соотношение положительно превышает положительное z-соотношение. Выходный сигнал дается, когда абсолютное значение z-соотношения меньше или равно другому (меньше по величине) порогу.

Для достижения этой ситуации необходимо знать, для каждой строки, является ли стратегия in или out рынка. long_market и short_market - это две переменные, определяемые для отслеживания длинных и коротких рыночных позиций. К сожалению, это намного проще кодировать итеративным способом, а не векторизированным подходом, и, следовательно, вычислять медленно. Несмотря на 1-минутные строки, требующие ~ 700 000 точек данных на CSV-файл, он все еще относительно быстрый для вычисления на моей старой настольной машине!

Для итерации над пандой DataFrame (которая, конечно, НЕ является обычной операцией) необходимо использовать метод iterrows, который предоставляет генератор, над которым итерация:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

На данном этапе мы обновили пары, чтобы содержать фактические длинные/короткие сигналы, что позволяет нам определить, нужно ли нам быть на рынке. Теперь нам нужно создать портфель, чтобы отслеживать рыночную стоимость позиций. Первая задача - создать колонку позиций, которая сочетает длинные и короткие сигналы. Это будет содержать список элементов от (1,0,−1), с 1 представляющим длинную/рыночную позицию, 0 представляющим никакую позицию (должен быть выпущен) и -1 представляющим короткую/рыночную позицию. Колонки sym1 и sym2 представляют рыночные значения позиций SPY и IWM при закрытии каждого бара.

После того, как рыночные значения ETF были созданы, мы суммируем их, чтобы получить общую рыночную стоимость в конце каждой строки. Это затем превращается в поток возврата методом pct_change для этого объекта Series. Последующие строки кода очищают плохие записи (элементы NaN и inf) и, наконец, вычисляют полную кривую собственности.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

ВглавныйФункция объединяет все. Внутренние CSV-файлы расположены на пути datadir. Убедитесь, что вы изменили код ниже, чтобы указать на ваш конкретный каталог.

Для того, чтобы определить, насколько чувствительна стратегия к периоду обратного просмотра, необходимо вычислить показатель производительности для диапазона обратных просмотров. Я выбрал окончательный общий процентный доход портфеля в качестве меры производительности и диапазон обратного просмотра в [50,200] с ступенями 10. Вы можете увидеть в следующем коде, что предыдущие функции завернуты в петлю for по всему этому диапазону, с другими порогами, удерживаемыми фиксированными.

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

Теперь можно увидеть график периода обратного обзора по отношению к доходам. Обратите внимание, что вокруг обратного обзора есть максимальный 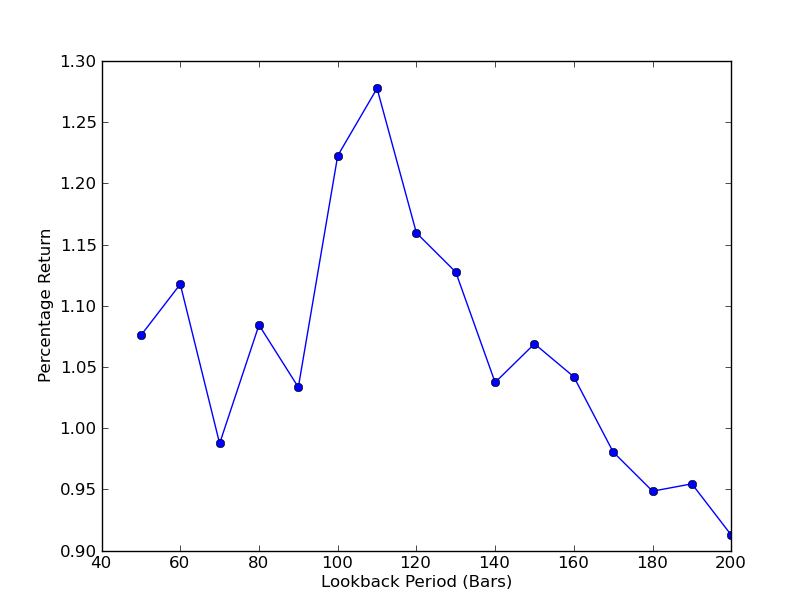global равный 110 бар. Если бы мы видели ситуацию, когда обратный обзор был независим от доходов, это было бы причиной для беспокойства:Линейная регрессия SPY-IWM - анализ чувствительности периода обзора соотношения хеджирования

Никакая статья по обратному тестированию не будет полной без кривой акций, наклоненной вверх! Таким образом, если вы хотите составить график кривой накопленной доходности по сравнению с временем, вы можете использовать следующий код. Он составит график окончательного портфеля, полученного из исследования параметров обратного взгляда. Таким образом, необходимо будет выбрать обратный взгляд в зависимости от того, какой график вы хотите визуализировать. График также содержит график доходности SPY за тот же период для облегчения сравнения:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

Нижеприведенный график кривой собственного капитала относится к 100-дневному периоду: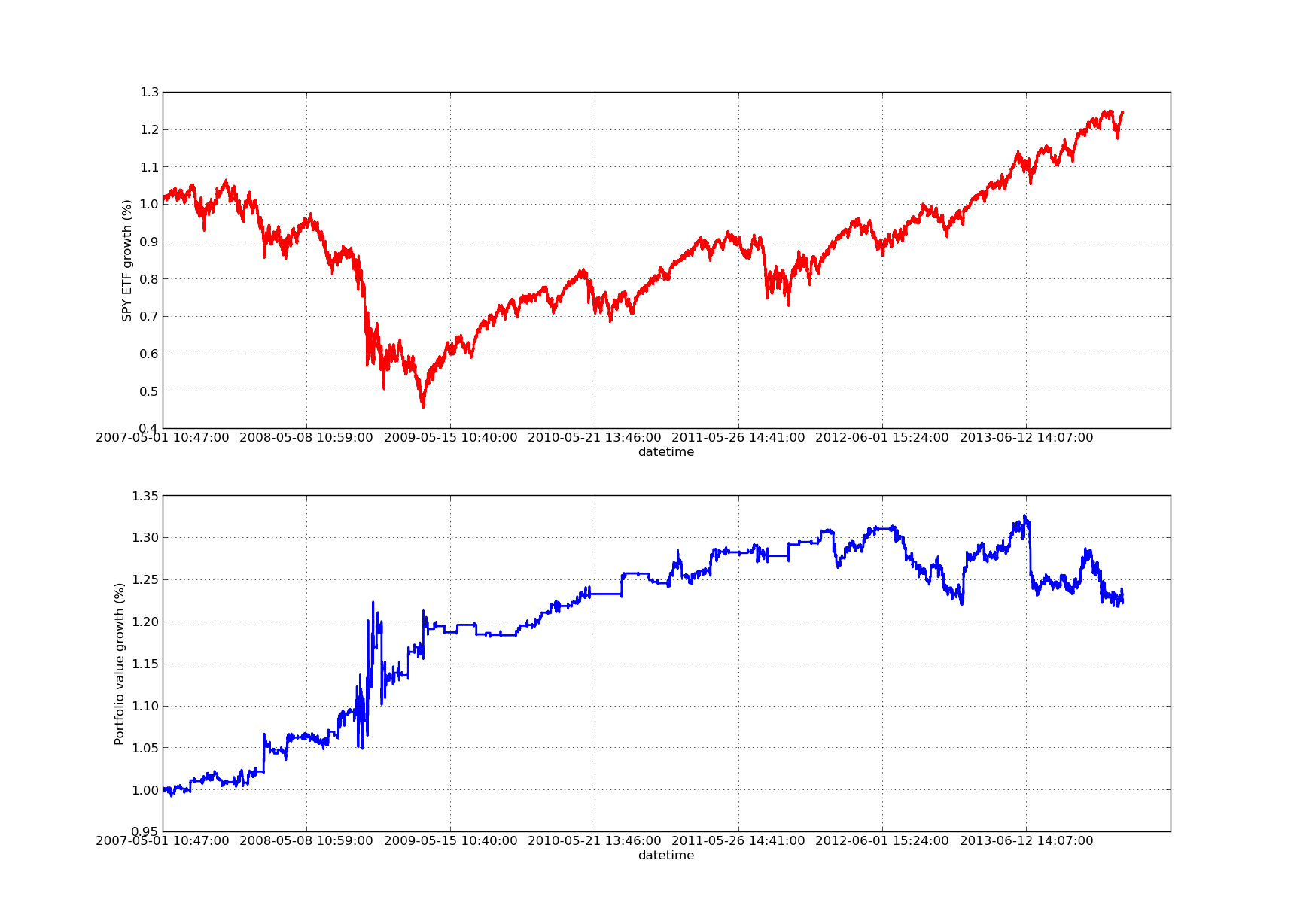Линейная регрессия SPY-IWM - анализ чувствительности периода обзора соотношения хеджирования

Следует отметить, что снижение SPY было значительным в 2009 году в период финансового кризиса. На этом этапе стратегия также пережила волатильный период. Также следует отметить, что показатели несколько ухудшились в прошлом году из-за сильного тенденционного характера SPY в этот период, что отражает индекс S&P500.

Следует отметить, что при расчете Z-оценки спреда мы все еще должны учитывать предвзятость взгляда. Кроме того, все эти расчеты были проведены без затрат на транзакции. Эта стратегия, безусловно, будет работать очень плохо, как только будут приняты во внимание эти факторы. В настоящее время не учитываются сборы, спред предложения / запроса и скольжение. Кроме того, стратегия торгуется в дробных единицах ETF, что также очень нереально.

В последующих статьях мы создадим гораздо более сложный обратный тест, основанный на событиях, который будет учитывать эти факторы и дает нам значительно больше уверенности в кривой собственности и показателях эффективности.