Примечание: данный случай используется для изучения и исследования, а не для инвестирования.

Данные о ценах на биткоин основаны на временной последовательности, поэтому прогнозы цен на биткоин в основном выполняются с использованием модели LSTM.

Долговременная кратковременная память (LSTM) - это модель глубокого обучения, особенно подходящая для данных временной последовательности (или данных, имеющих временную / пространственную / структурную последовательность, например, фильмы, предложения и т. Д.), Идеальная модель для прогнозирования ценового направления криптовалюты.

В статье рассматриваются данные, полученные в результате сопоставления данных с помощью LSTM, которые позволяют прогнозировать будущую цену биткоина.

Библиотека, которую нужно использовать для импорта

            
            
            
import pandas as pd
import numpy as np

from sklearn.preprocessing import MinMaxScaler, LabelEncoder
from keras.models import Sequential
from keras.layers import LSTM, Dense, Dropout

from matplotlib import pyplot as plt
%matplotlib inline

Анализ данных

Загрузка данных

Читать данные о дневном обороте BTC

            
            
            
data = pd.read_csv(filepath_or_buffer="btc_data_day")

В настоящее время существует 1380 данных, состоящих из столбцов Date, Open, High, Low, Close, Volume (BTC), Volume (Currency) и Weighted Price. Кроме столбца Date, все остальные столбцы имеют тип данных float64.

            
            
            
data.info()

Посмотрите на первые 10 строк данных.

            
            
            
data.head(10)

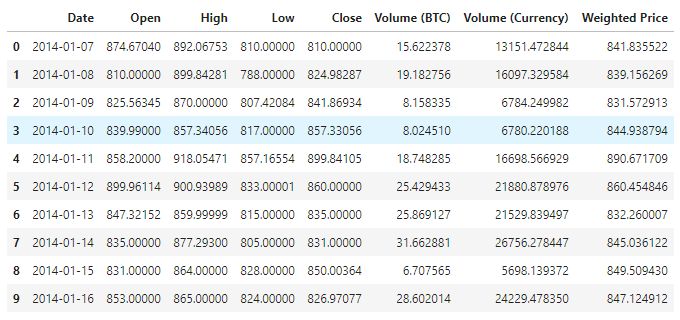
Визуализация данных

Используйте matplotlib, чтобы нанести на карту весовую цену, чтобы увидеть, как распределены данные и как они движутся. На графике мы обнаружили часть данных 0, и нам нужно подтвердить, есть ли какие-либо исключения в данных.

            
            
            
plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

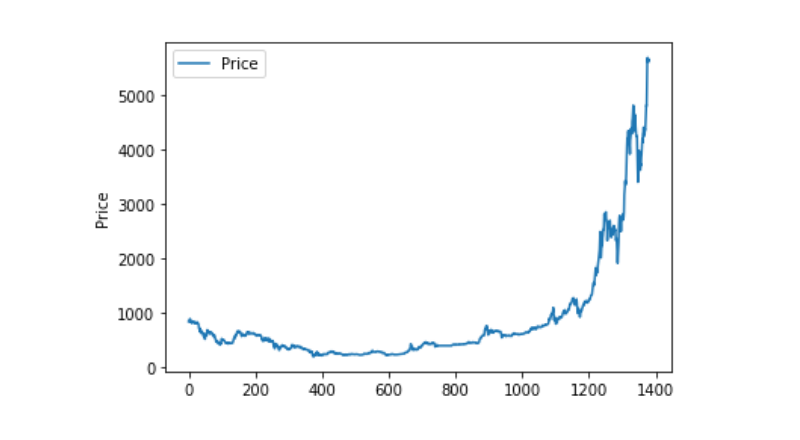
Необычная обработка данных

Сначала посмотрим, есть ли в данных данные нана, и мы увидим, что в наших данных нет данных нана.

            
            
            
data.isnull().sum()

            
            
            
Date                 0
Open                 0
High                 0
Low                  0
Close                0
Volume (BTC)         0
Volume (Currency)    0
Weighted Price       0
dtype: int64

Теперь посмотрим на нулевую величину, и мы увидим, что она содержит нулевую величину, и мы должны обрабатывать нулевую величину.

            
            
            
(data == 0).astype(int).any()

            
            
            
Date                 False
Open                  True
High                  True
Low                   True
Close                 True
Volume (BTC)          True
Volume (Currency)     True
Weighted Price        True
dtype: bool

            
            
            
data['Weighted Price'].replace(0, np.nan, inplace=True)
data['Weighted Price'].fillna(method='ffill', inplace=True)
data['Open'].replace(0, np.nan, inplace=True)
data['Open'].fillna(method='ffill', inplace=True)
data['High'].replace(0, np.nan, inplace=True)
data['High'].fillna(method='ffill', inplace=True)
data['Low'].replace(0, np.nan, inplace=True)
data['Low'].fillna(method='ffill', inplace=True)
data['Close'].replace(0, np.nan, inplace=True)
data['Close'].fillna(method='ffill', inplace=True)
data['Volume (BTC)'].replace(0, np.nan, inplace=True)
data['Volume (BTC)'].fillna(method='ffill', inplace=True)
data['Volume (Currency)'].replace(0, np.nan, inplace=True)
data['Volume (Currency)'].fillna(method='ffill', inplace=True)

            
            
            
(data == 0).astype(int).any()

            
            
            
Date                 False
Open                 False
High                 False
Low                  False
Close                False
Volume (BTC)         False
Volume (Currency)    False
Weighted Price       False
dtype: bool

Теперь посмотрим на распределение и движение данных, и на этом этапе кривая будет очень последовательной.

            
            
            
plt.plot(data['Weighted Price'], label='Price')
plt.ylabel('Price')
plt.legend()
plt.show()

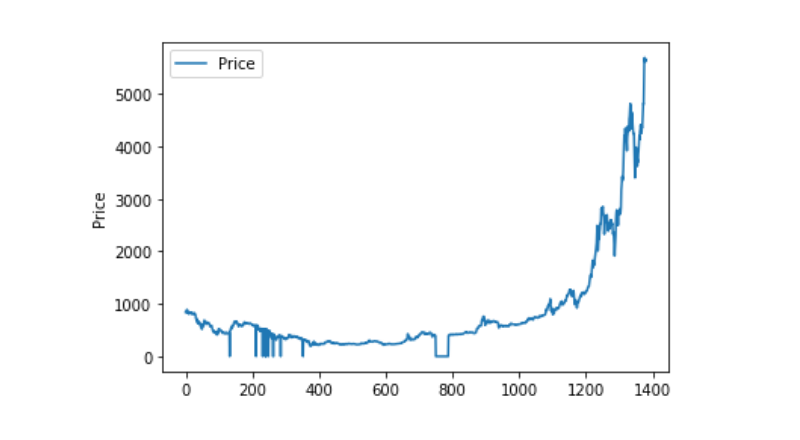
Разделение на тренировочные и тестовые

Однообразить данные в 0-1

            
            
            
data_set = data.drop('Date', axis=1).values
data_set = data_set.astype('float32')
mms = MinMaxScaler(feature_range=(0, 1))
data_set = mms.fit_transform(data_set)

Разделение тестовых и тренировочных наборов данных на 2:8

            
            
            
ratio = 0.8
train_size = int(len(data_set) * ratio)
test_size = len(data_set) - train_size
train, test = data_set[0:train_size,:], data_set[train_size:len(data_set),:]

Создание тренировочных и тестовых наборов данных, используя один день в качестве окна для создания наших тренировочных и тестовых наборов данных.

            
            
            
def create_dataset(data):
    window = 1
    label_index = 6
    x, y = [], []
    for i in range(len(data) - window):
        x.append(data[i:(i + window), :])
        y.append(data[i + window, label_index])
    return np.array(x), np.array(y)

            
            
            
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Определение модели и обучение

В этот раз мы используем простую модель, которая выглядит следующим образом:. LSTM2. Dense。

Здесь нужно сделать пояснение к inputh shape LSTM, входное измерение Input Shape составляет ((batch_size, time steps, features)). В данном случае, значение time steps является интервалом временного окна во время ввода данных, здесь мы используем 1 день в качестве временного окна, и наши данные являются дневными данными, поэтому наши временные шаги здесь равны 1 ‒

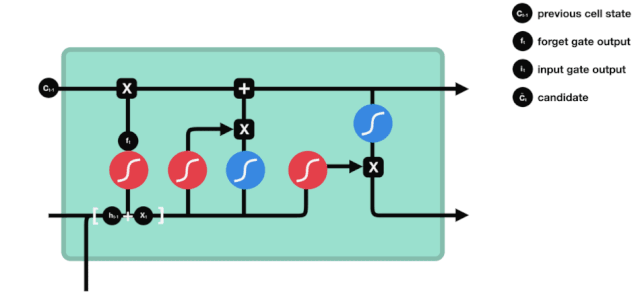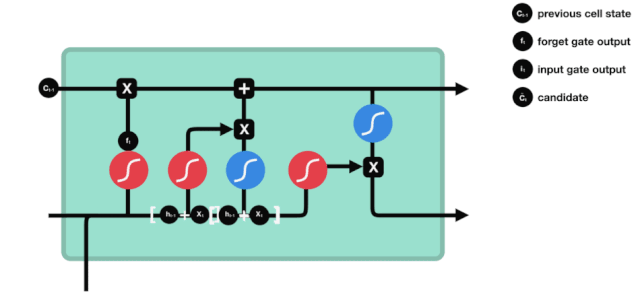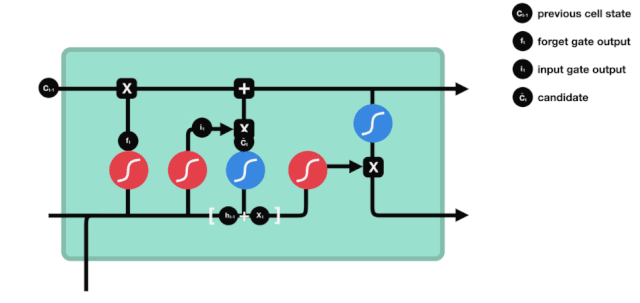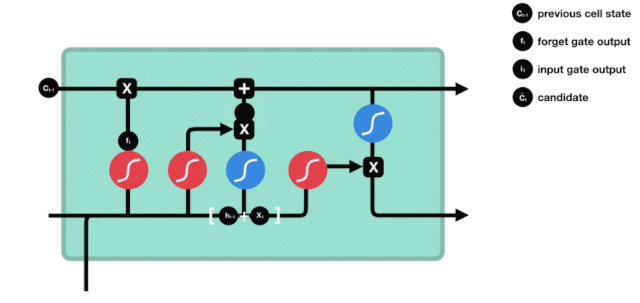
Долгая краткосрочная память (LSTM) - специальный тип RNN, используемый для решения проблем исчезновения и взрыва градиентов в процессе обучения длинным последовательностям.

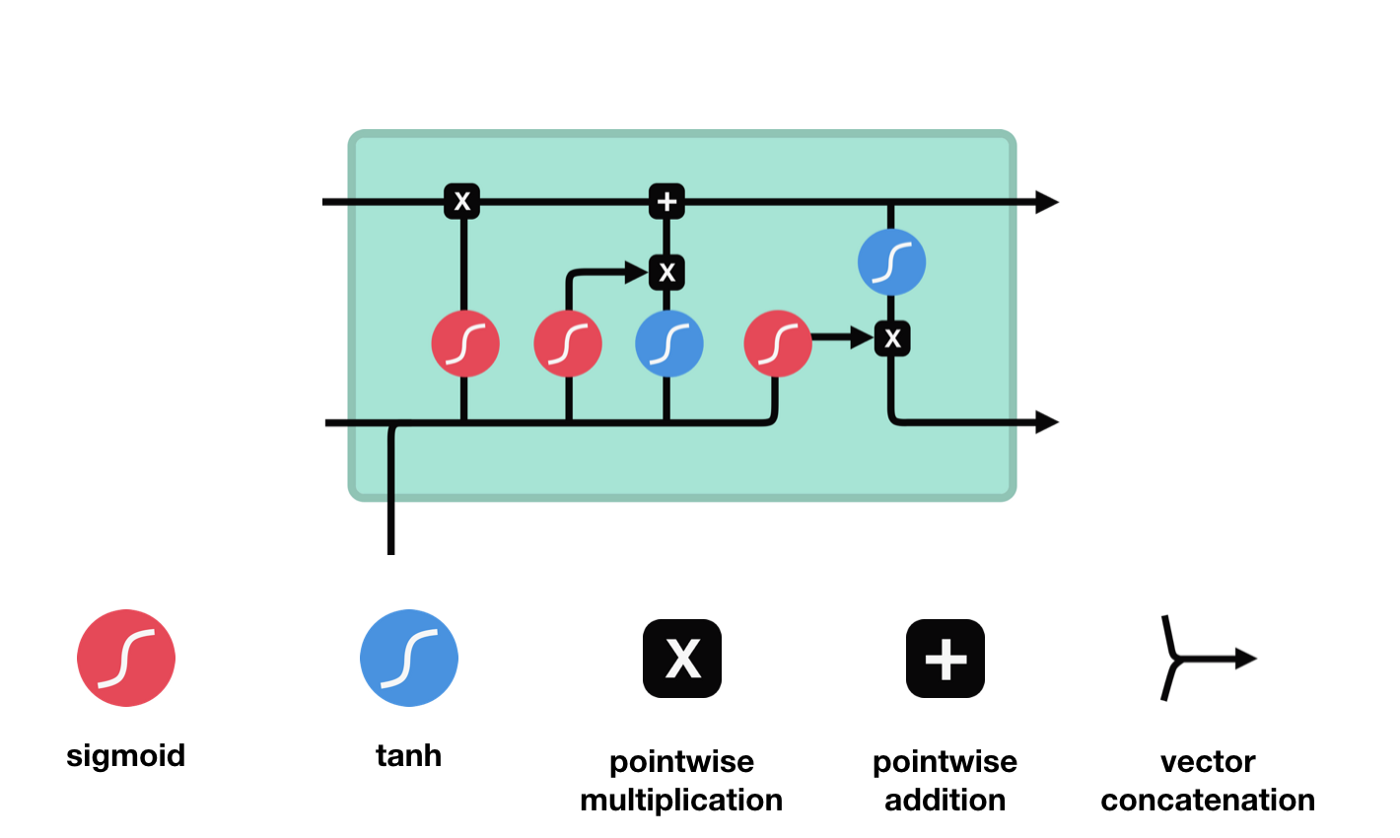
Из схемы сетевой структуры LSTM можно увидеть, что LSTM - это небольшая модель, которая включает в себя 3 сигмоидных активационных функции, 2 танх-активационные функции, 3 умножения и 1 сложение.

Состояние клетки

Клеточный статус является центральным элементом LSTM, он представляет собой верхнюю черную линию на рисунке. Ниже этой черной линии находятся двери, о которых мы расскажем в дальнейшем.

Сеть LSTM позволяет удалять или добавлять информацию о состоянии клеток через структуру, называемую воротами. Врата позволяют избирательно решать, какую информацию пропускать. Структура ворот - это сигмоидный слой и комбинация операций умножения точек.

Врата забвения

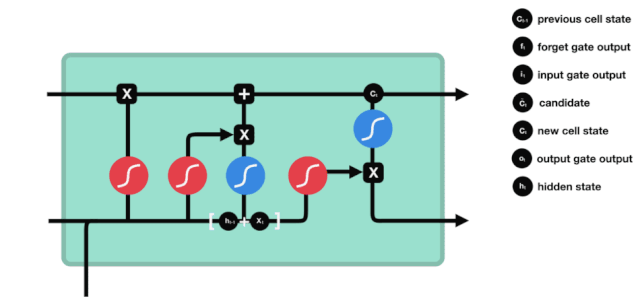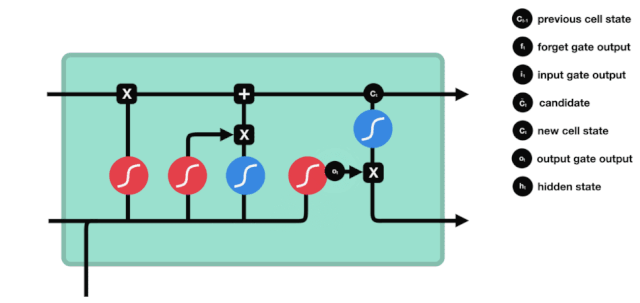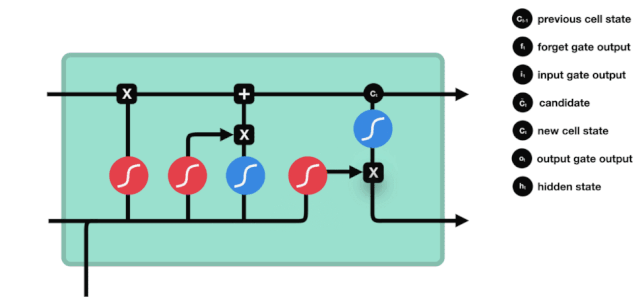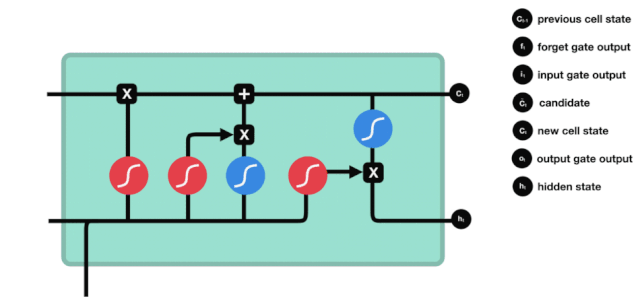
Первым шагом LSTM является определение того, какую информацию нужно удалить из клеточного состояния. Эта часть операции обрабатывается посредством сигмоидной ячейки, называемой дверью забвения.

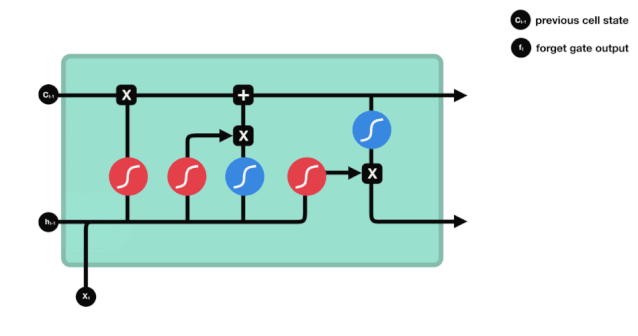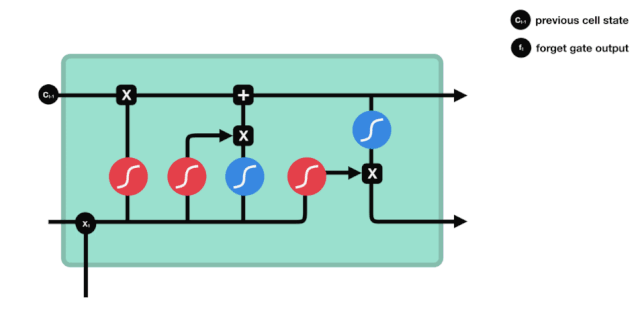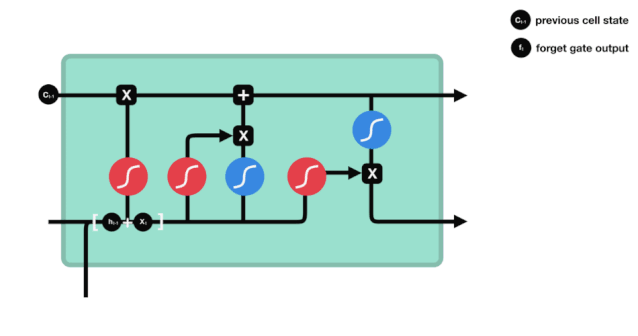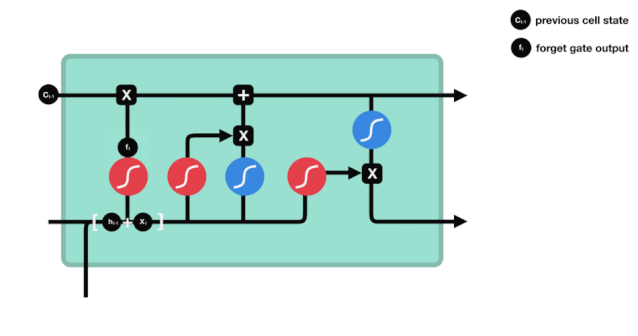
Мы можем видеть, что шлюз забвения, просматривая информацию \(h_{l-1}\) и \(x_{t}\), выводит вектор между 0 и 1, где значение 0 в векторе указывает на то, какая информация сохраняется или отбрасывается из состояния клетки \(C_{t-1}\). 0 означает, что она не сохраняется, и 1 означает, что она сохраняется.

Математическое выражение: \(f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)\)

Входные двери

Следующим шагом является определение того, какую новую информацию можно добавить к состоянию клетки, и это делается путем ввода и открытия входа.

Мы видим, что \(h_{l-1}\) и \(x_{t}\) были помещены в забытое (sigmoid) и входное (tanh) ворота. Поскольку выходное значение забытого ворота - 0-0, то, если забытое ворота - 0, то входное значение \(C_{i}\) не будет добавлено в текущее состояние ячейки, а если 1, то все будет добавлено в состояние ячейки, поэтому забытое ворота будет выборочно добавлять входное значение в состояние ячейки.

Математическая формула: \(C_{t}=f_{t} * C_{t-1}+i_{t} *\tilde{C}_{t}\)

Выход

После обновления состояния клетки необходимо судить, какие состояния выходной клетки характеризуются суммой \(h_{l-1}\) и \(x_{t}\) входов. Здесь нужно оценить вход через сигмоидный слой, называемый выходной дверью, а затем оценить состояние клетки через таньский слой, чтобы получить вектор с значениями от -1 до 1, этот вектор умножен на выходной дверь, чтобы получить выходной элемент этой конечной RNN.

            
            
            
def create_model():
    model = Sequential()
    model.add(LSTM(50, input_shape=(train_x.shape[1], train_x.shape[2])))
    model.add(Dense(1))
    model.compile(loss='mae', optimizer='adam')
    model.summary()
    return model

model = create_model()

            
            
            
history = model.fit(train_x, train_y, epochs=80, batch_size=64, validation_data=(test_x, test_y), verbose=1, shuffle=False)

            
            
            
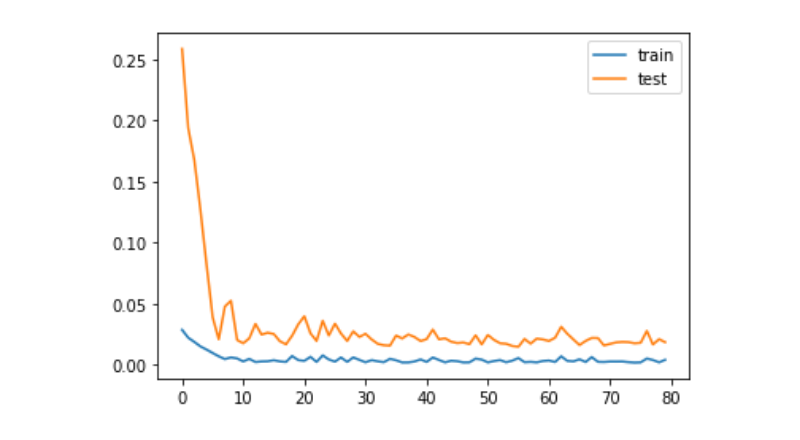
plt.plot(history.history['loss'], label='train')
plt.plot(history.history['val_loss'], label='test')
plt.legend()
plt.show()

            
            
            
train_x, train_y = create_dataset(train)
test_x, test_y = create_dataset(test)

Прогноз

            
            
            
predict = model.predict(test_x)
plt.plot(predict, label='predict')
plt.plot(test_y, label='ground true')
plt.legend()
plt.show()

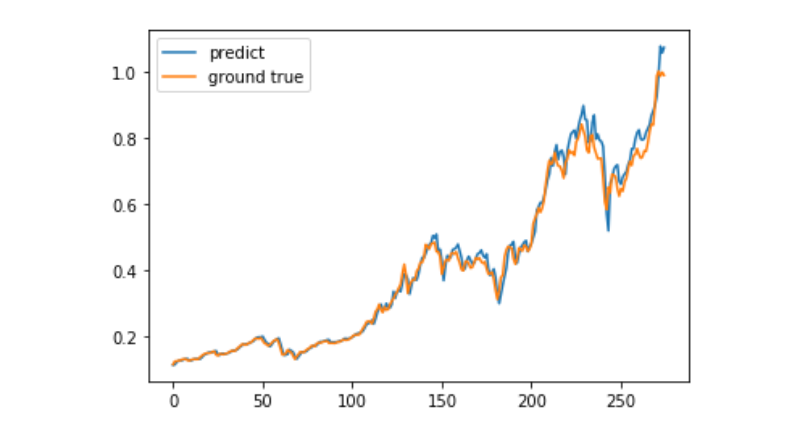
В настоящее время использование машинного обучения для прогнозирования долгосрочного ценового движения биткоина является очень трудным, и этот текст может быть использован только в качестве учебного случая. Этот случай будет запущен в режиме реального времени в виде демо-изображений в облаке Метриковых прудов, и заинтересованные пользователи могут непосредственно испытать его.