Стратегия внутридневной торговли, использующая равнозначное возвращение между SPY и IWM

В данной статье мы рассмотрим стратегию внутридневного торговли. Она будет использовать классическую торговую идею, которая заключается в том, чтобы торговать парой пары с равной стоимостью рентабельности. В этом примере мы будем использовать два открытых индексальных фонда (ETF), SPY и IWM, которые торгуют на Нью-Йоркской фондовой бирже (NYSE) и пытаются представлять индексы американских фондовых рынков, S&P 500 и Russell 2000 соответственно.

Эта стратегия создает разницу в прибыли, делая больше одного ETF и делая другой ETF неактивным. Многопространственное соотношение может быть определено многими способами, например, с использованием методов статистических синхронных временных последовательностей. В этом случае мы будем рассчитывать соотношение хеджировки между SPY и IWM с помощью линейного регрессия. Это позволит нам создать разницу в прибыли между SPY и IWM, которая будет стандартизирована как z-score. Когда z-score превышает определенный порог, будет произведен торговый сигнал, поскольку мы верим, что разница в прибыли вернется к среднему значению.

Основной принцип этой стратегии заключается в том, что SPY и IWM представляют собой примерно одну и ту же рыночную ситуацию, а именно, цены на акции группы крупных и малых американских компаний. Предполагается, что если принять теорию регрессивной вертикали, то она всегда возвращается, поскольку вертикали могут влиять на S&P 500 и Russell 2000 в короткие сроки, но разница в прибыли между ними всегда возвращается к нормальному среднему, и длительные цепочки цен всегда сочетаются ("все вместе интегрированы").

Стратегия

Эта стратегия выполняется следующими шагами:

Данные - 1-минутные к-схемы SPY и IWM, полученные с апреля 2007 по февраль 2014 года.

Обработка - правильное выравнивание данных и удаление взаимно отсутствующих k-строчек.

Дифференциация - соотношение хеджирования между двумя ETF с использованием роликового линейного регрессионного расчета. Определяется как коэффициент регрессии β с использованием регрессионного окна, которое перемещает 1 корень к линии вперед и пересчитывает коэффициент регрессии. Таким образом, соотношение хеджирования βi, корень би-К-линии используется для регрессии к линии путем расчета пересечения от bi-1-k до bi-1, чтобы перейти к линии k.

Z-Score - значение стандартной разницы рассчитывается обычным способом. Это означает, что вычитается среднее значение стандартной разницы и вычитается стандартная разница с использованием прибыли. Причина этого заключается в том, чтобы сделать параметры порога более понятными, поскольку Z-Score является безмерной величиной.

Торговля - когда значение отрицательного z-score снижается ниже заданного (или оптимизированного) порога, то появляется больше сигнал, а сигнал пустого действия - наоборот. Когда абсолютное значение z-score снижается ниже дополнительного порога, то появляется сигнал тирании. Для этой стратегии я (несколько случайно) выбрал z-score = 2 как порог открытия, а z-score = 1 как порог тирании. Предположим, что равномерные возвраты играют роль в разнице прибыли.

Возможно, лучший способ глубже понять политику - это реализовать ее на практике. В следующем разделе подробно описан полный код Python для реализации этой стратегии возвращения равнозначных значений ("один файл"). Я добавил подробные кодовые комментарии, чтобы помочь вам лучше понять.

Реализация Python

Как и все учебные пособия по Python/pandas, они должны быть настроены в соответствии с Python-окружением, описанным в этом учебном пособии. После завершения настройки первая задача - импортировать необходимую библиотеку Python. Это необходимо для использования matplotlib и pandas.

Я использую следующую версию библиотеки:

Python - 2.7.3 NumPy - 1.8.0 Панды - 0.12.0 Matplotlib - 1.1.0

Давайте продолжим и введем следующие библиотеки:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Следующая функция create_pairs_dataframe импортирует в CSV-файл две внутриквартальные строки, содержащие два символа. В нашем примере это будет SPY и IWM. Затем она создает отдельную пару пары пары пары данных, которая будет использовать индексы двух первичных файлов. Из-за пропущенных сделок и ошибок их сроки могут отличаться.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Следующим шагом является прокат линейного регрессирования между SPY и IWM. В этом сценарии IWM является прогнозирующим (x), SPY - ответом (y). Я установил кнопка регрессии по умолчанию на 100 к-строков. Это параметры политики, как указано выше. Для того, чтобы политика считалась надежной, мы, в идеале, хотели бы видеть возвращающийся отчет, который в регрессивном периоде демонстрирует состояние выпуклой (x) или другие показатели производительности.

После вычисления коэффициента β в линейной регрессионной модели SPY-IWM, добавляем его в DataFrame и удаляем пробелы. Это создает первую группу K-линий, которая равна ретроспективному размеру обрезки длины. Затем мы создаем два разрыва ETF в единицах SPY и в единицах -βi IWM. Очевидно, это не реально, потому что мы используем небольшое количество IWM, что невозможно в практической реализации.

Наконец, мы создаем z-счет прибыли, который рассчитывается путем вычитания среднего размера прибыли и стандартного стандартного размера прибыли. Следует отметить, что здесь существует довольно тонкая форма прогрессивного отклонения. Я намеренно оставил ее в коде, потому что хочу подчеркнуть, как легко совершать такие ошибки в исследованиях.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

В create_long_short_market_signals создаются торговые сигналы. Они рассчитываются как значение z-score, превышающее порог.

Для достижения этого необходимо установить для каждой строки k стратегию торговли - открытый или плоский; long_market и short_market - две переменные, которые определяются для отслеживания многозадачных и пустых позиций. К сожалению, программирование в итерационном режиме проще, чем в векторальном методе, и поэтому вычисления медленные. Хотя для 1 минутной строки k требуется около 700 000 точек данных на CSV-файл, на моем старом настольном компьютере это все еще относительно быстро!

Для иридации пандас DataFrame (это, несомненно, необычная операция) необходимо использовать метод iterrows, который предоставляет иридирующий генератор:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

На этом этапе мы обновили пары, чтобы включить реальные много, пустые сигналы, что позволило нам определить, нужно ли нам открывать позиции. Теперь нам нужно создать портфель, чтобы отслеживать рыночную стоимость позиций. Первая задача - создать позиционный столб, объединяющий многоголовые сигналы и пустые сигналы.

После того, как была создана рыночная стоимость ЭТФ, мы сравниваем их, чтобы получить общую рыночную стоимость в конце каждой строки k. Затем мы преобразуем ее в возвращаемую стоимость с помощью pct_change метода этого объекта. Последующие строки кода удаляют неправильные записи ((NaN и элементы inf), и, наконец, рассчитываем полную кривую прибыли.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Основная функция объединяет их. В данном случае CSV-файл находится в пути datadir. Пожалуйста, не забудьте изменить следующий код, чтобы указать на ваш конкретный каталог.

Для определения чувствительности стратегии к циклам lookback необходимо вычислить ряд показателей производительности lookback. Я выбрал процент конечного общего дохода портфеля в качестве показателя производительности и lookback range[50,200], увеличенный на 10. Вы можете увидеть в следующем коде, что предыдущая функция содержится в цикле for в этом диапазоне, другие пороги остаются неизменными.

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

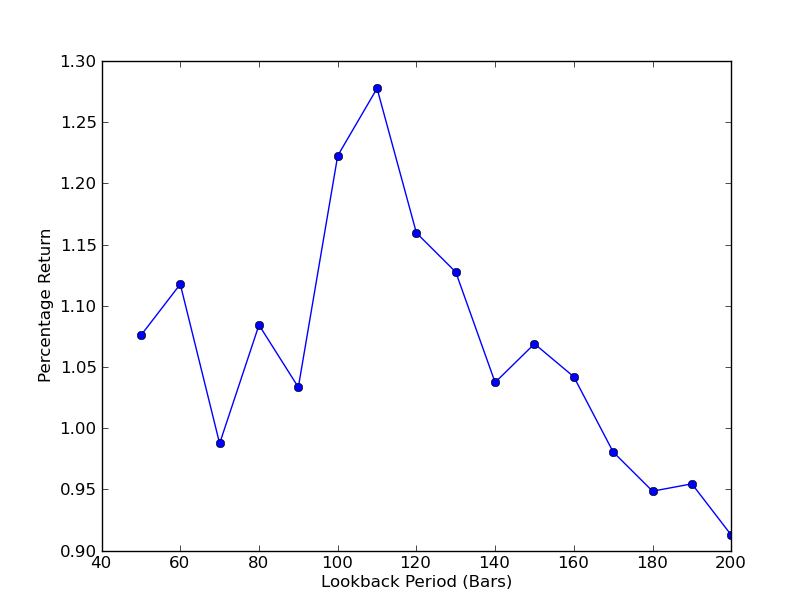
Теперь можно увидеть график lookbacks и returns. Обратите внимание, что lookback имеет максимальное значение цепочки, равное 110 к-строкам. Если мы видим, что lookbacks не связаны с returns, это потому, что:

SPY-IWM линейный регрессионный хеджирование по сравнению с анализом чувствительности на период lookback

Без наклонной вверх кривой прибыли любой ретроспективный пост будет неполным! Поэтому, если вы хотите нарисовать кривую совокупной прибыли и времени, вы можете использовать следующий код. Он будет рисовать конечный портфель инвестиций, полученный из исследования параметров lookback. Таким образом, необходимо выбрать lookback в соответствии с графиком, который вы хотите визуализировать.

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Например, в 2010 году в Китае было установлено, что в течение следующих 100 дней будет наблюдаться следующая тенденция:

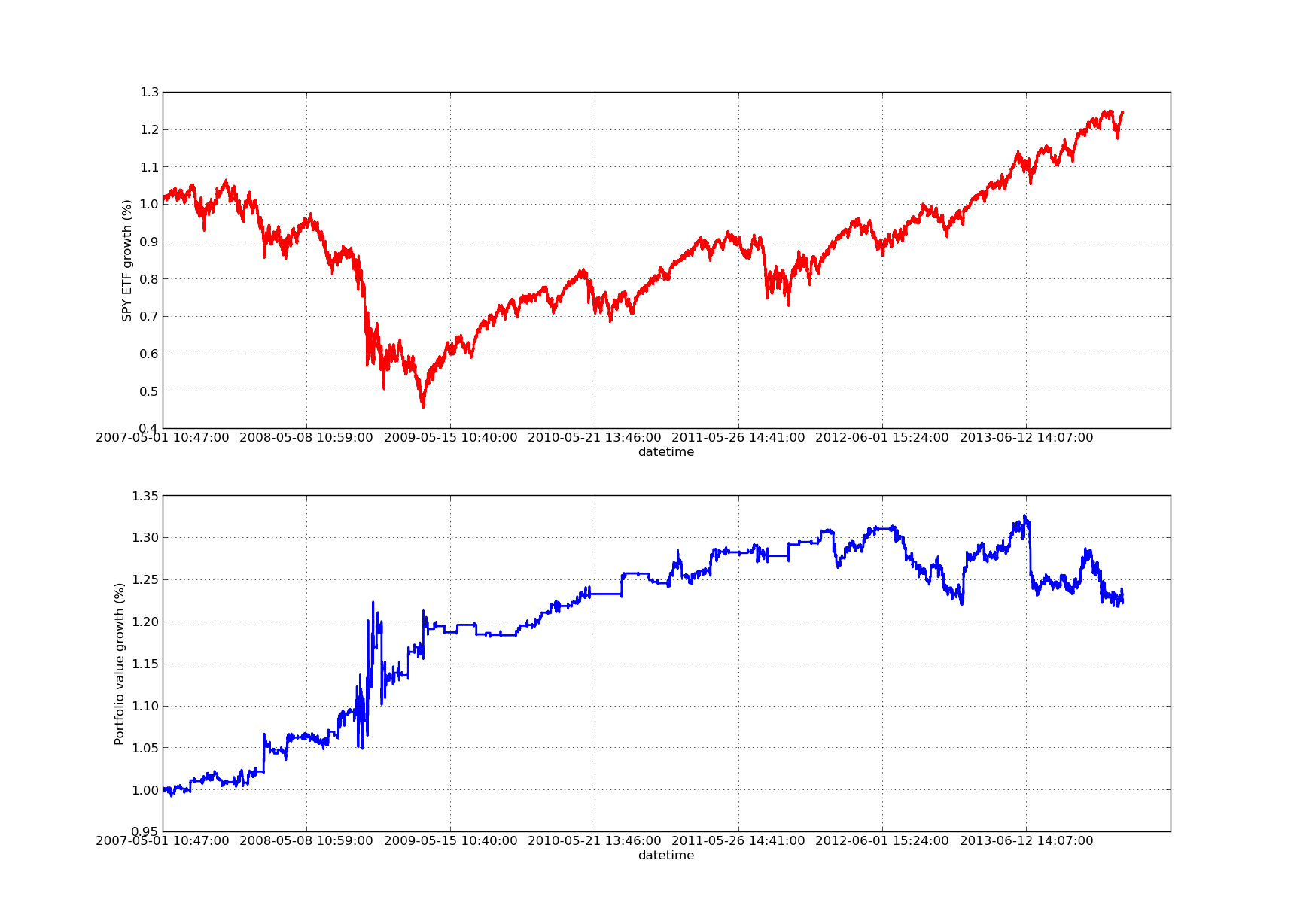
SPY-IWM линейный регрессионный хеджирование по сравнению с анализом чувствительности на период lookback

Обратите внимание, что в 2009 году SPY значительно сократился во время финансового кризиса. Эта стратегия также находилась в нестабильном состоянии на этом этапе. Обратите также внимание, что в прошлом году показатели ухудшились из-за сильного тенденционного характера SPY в этот период, отражающего индекс S&P 500.

Обратите внимание, что при расчете Z-score мы все еще должны учитывать перспективное отклонение. Кроме того, все эти расчеты были сделаны без затрат на транзакции. С учетом этих факторов эта стратегия, безусловно, будет плохо работать.

В последующих статьях мы будем создавать более сложный эпизодический backtester, который будет учитывать эти факторы, чтобы дать нам больше уверенности в кривой капитала и показателях производительности.