Парная торговля — отличный пример разработки торговой стратегии на основе математического анализа. В этой статье мы покажем, как использовать данные для создания и автоматизации стратегии парной торговли.

Основные принципы

Предположим, у вас есть пара инвестиций X и Y, которые имеют некоторую базовую корреляцию, например, обе компании производят один и тот же продукт, например Pepsi и Coca-Cola. Вы хотите, чтобы соотношение цен или базис (также называемый спредом) между ними оставалось постоянным с течением времени. Однако спред между двумя парами может время от времени расходиться из-за временных изменений спроса и предложения, таких как крупные ордера на покупку/продажу для одной инвестиционной цели, реакция на важные новости об одной из компаний и т. д. В этом случае одна инвестиция движется вверх, а другая вниз относительно друг друга. Если вы ожидаете, что это расхождение со временем нормализуется, вы можете заметить торговую возможность (или возможность арбитража). Подобные арбитражные возможности есть повсюду на рынке цифровых валют или внутреннем рынке товарных фьючерсов, например, взаимосвязь между BTC и активами-убежищами; взаимосвязь между соевым шротом, соевым маслом и сортами сои во фьючерсах.

Когда есть временная разница в цене, сделка продаст преуспевающую инвестицию (инвестицию, которая выросла) и купит неэффективную инвестицию (инвестицию, которая упала). Вы можете быть уверены, что между двумя инвестициями есть разница. Спред в конечном итоге будет отражен падением опережающих инвестиций или ростом неэффективных инвестиций, или обоими. Ваша торговля принесет прибыль во всех этих сценариях. Если инвестиции будут расти или падать одновременно, не меняя разницы между ними, вы не заработаете и не потеряете деньги.

Таким образом, парная торговля представляет собой рыночно-нейтральную торговую стратегию, которая позволяет трейдерам получать прибыль практически из любых рыночных условий: восходящего, нисходящего или бокового тренда.

Объясните концепцию: две гипотетические цели инвестиций

• Создание нашей исследовательской среды на платформе Inventor Quantitative

Прежде всего, чтобы работать гладко, нам нужно построить нашу исследовательскую среду. В этой статье мы используем Inventor Quantitative Platform (FMZ.COM) для построения исследовательской среды, в основном для того, чтобы мы могли использовать удобный и быстрый API Интерфейс и инкапсуляция этой платформы позже. Полная система Docker.

В официальном названии Inventor Quantitative Platform эта система Docker называется хост-системой.

Более подробную информацию о том, как развертывать хосты и роботов, можно найти в моей предыдущей статье: https://www.fmz.com/bbs-topic/4140

Читатели, желающие приобрести собственный хост для развертывания сервера облачных вычислений, могут обратиться к этой статье: https://www.fmz.com/bbs-topic/2848

После успешного развертывания сервиса облачных вычислений и хост-системы мы установим самый мощный инструмент Python: Anaconda.

Чтобы реализовать все необходимые для этой статьи программные среды (зависимые библиотеки, управление версиями и т. д.), проще всего использовать Anaconda. Это пакетная экосистема Python для обработки и анализа данных, а также менеджер зависимостей.

Информацию о способе установки Anaconda см. в официальном руководстве Anaconda: https://www.anaconda.com/distribution/

В этой статье также будут использоваться numpy и pandas — две очень популярные и важные библиотеки в научных вычислениях на Python.

Для вышеприведенной базовой работы вы также можете обратиться к моей предыдущей статье, в которой рассказывается, как настроить среду Anaconda и две библиотеки numpy и pandas. Подробности см.: https://www.fmz.com/digest- тема/4169

Далее, давайте воспользуемся кодом для реализации «двух гипотетических инвестиционных целей».

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Да, мы также будем использовать matplotlib, очень известную библиотеку диаграмм на Python.

Давайте создадим гипотетический инвестиционный актив X и смоделируем построение графика его ежедневной доходности с использованием нормального распределения. Затем мы выполняем кумулятивное суммирование, чтобы получить ежедневное значение X.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

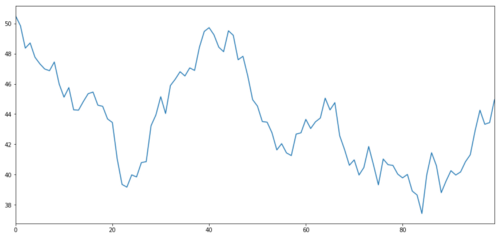
Инвестиционная цель X, смоделируйте и получите ее ежедневную доходность через нормальное распределение

Теперь мы генерируем Y, который сильно коррелирует с X, поэтому цена Y должна изменяться очень похоже на изменения X. Мы моделируем это, беря X, сдвигая его вверх и добавляя некоторый случайный шум, взятый из нормального распределения.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

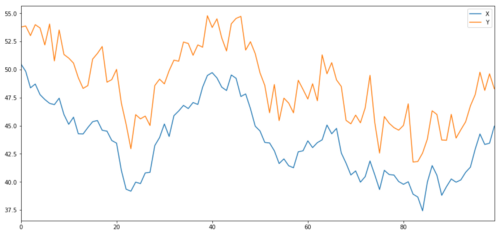
Коинтеграция инвестиционных целей X и Y

Коинтеграция

Коинтеграция очень похожа на корреляцию, что означает, что соотношение между двумя рядами данных будет варьироваться вокруг среднего. Два ряда Y и X следуют следующему:

Y = ⍺ X + e

где ⍺ — постоянное отношение, а e — шум.

Для торговой пары между двумя временными рядами ожидаемое значение отношения с течением времени должно сходиться к среднему значению, т. е. они должны быть коинтегрированы. Временные ряды, которые мы построили выше, являются коинтегрированными. Теперь нарисуем шкалу между ними, чтобы увидеть, как это будет выглядеть.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

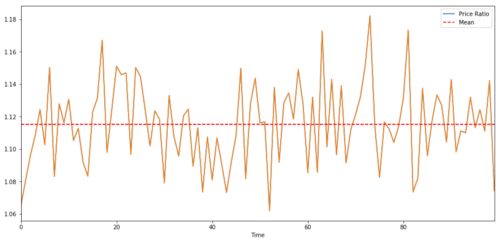
Соотношение и среднее значение цен двух коинтегрированных инвестиций

Тест на коинтеграцию

Удобный способ проверить это — использовать statsmodels.tsa.stattools. Мы должны увидеть очень низкое p-значение, поскольку мы искусственно создали два ряда данных, которые максимально коинтегрированы.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Результат: 1.81864477307e-17

Примечание: корреляция и коинтеграция

Хотя корреляция и коинтеграция теоретически схожи, это не одно и то же. Давайте рассмотрим примеры рядов данных, которые коррелируют, но не коинтегрированы, и наоборот. Сначала давайте проверим корреляцию только что сгенерированного нами ряда.

X.corr(Y)

Результат: 0,951

Как мы и ожидали, этот показатель очень высок. Но как быть с двумя рядами, которые коррелируют, но не коинтегрированы? Простой пример — два расходящихся ряда данных.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

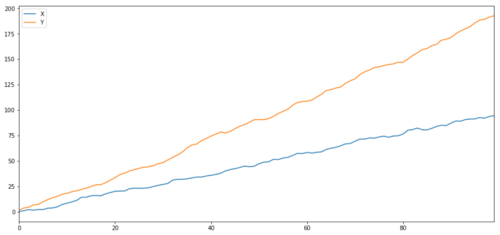
Две связанные серии (не коинтегрированные)

Коэффициент корреляции: 0,998 Значение p для теста коинтеграции: 0,258

Простыми примерами коинтеграции без корреляции являются нормально распределенный ряд и прямоугольная волна.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()

Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

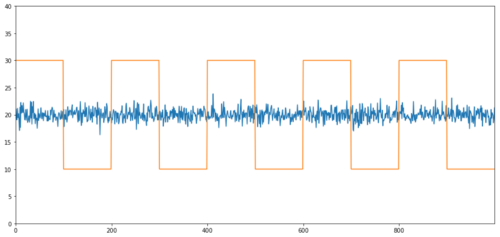
Корреляция: 0,007546 Значение p теста коинтеграции: 0,0

Корреляция очень низкая, но p-значение показывает идеальную коинтеграцию!

Как заниматься парной торговлей?

Поскольку два коинтегрированных временных ряда (например, X и Y выше) движутся друг к другу и друг от друга, бывают моменты, когда существует высокий базис и низкий базис. Мы осуществляем парную торговлю, покупая одну инвестицию и продавая другую. Таким образом, если две инвестиционные цели падают или растут одновременно, мы не зарабатываем и не теряем деньги, то есть мы нейтральны к рынку.

Возвращаясь к X и Y в Y = ⍺ X + e выше, мы зарабатываем деньги, заставляя отношение (Y/X) двигаться вокруг своего среднего значения ⍺. Для этого отметим, что когда X Когда значение ⍺ слишком высокое или слишком низкое, значение ⍺ слишком высокое или слишком низкое:

• Длинное отношение: это когда отношение ⍺ мало, и мы ожидаем, что оно увеличится. В приведенном выше примере мы открываем позицию, покупая Y и продавая X.

• Короткое отношение: это когда отношение ⍺ велико, и мы ожидаем, что оно станет меньше. В приведенном выше примере мы открываем позицию, продавая короткую позицию Y и длинную позицию X.

Обратите внимание, что у нас всегда есть «хеджированная позиция»: если базовая длинная позиция теряет стоимость, короткая позиция приносит прибыль, и наоборот, поэтому мы невосприимчивы к общим движениям рынка.

Поскольку активы X и Y движутся относительно друг друга, мы зарабатываем или теряем деньги.

Используйте данные для поиска транзакций с похожим поведением

Лучший способ сделать это — начать со сделок, которые, по вашему мнению, могут быть коинтегрированы, и провести статистические тесты. Если вы проведете статистический тест по всем торговым парам, вы будетеСмещение множественных сравненийжертва.

Смещение множественных сравненийотносится к ситуации, когда вероятность ложной генерации значимого p-значения увеличивается при запуске большого количества тестов, поскольку нам необходимо запустить большое количество тестов. Если мы запустим этот тест 100 раз на случайных данных, мы должны увидеть 5 значений p ниже 0,05. Если вы сравниваете n инструментов для коинтеграции, вы будете выполнять n(n-1)/2 сравнений и увидите много неверных p-значений, которые будут увеличиваться по мере увеличения размера вашей тестовой выборки. И увеличиваться. Чтобы избежать этого, выберите несколько торговых пар, которые, по вашему мнению, могут быть коинтегрированы, а затем протестируйте их по отдельности. Это значительно сократитСмещение множественных сравнений。

Давайте попробуем найти инструменты, которые демонстрируют коинтеграцию. Давайте возьмем корзину акций американских технологических компаний с большой капитализацией в S&P 500. Эти инструменты работают в схожих сегментах рынка и демонстрируют коинтеграцию. цена. Мы сканируем список торговых инструментов и проверяем коинтеграцию между всеми парами.

Включены возвращенная матрица результатов теста коинтеграции, матрица p-значений и все попарные совпадения со значением p менее 0,05.Этот метод подвержен множественным сравнительным ошибкам, поэтому на практике необходимо проводить повторную проверку. В данной статье для удобства объяснения мы решили проигнорировать это в примерах.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Примечание: Мы включили в наши данные рыночный бенчмарк (SPX) — рынок движет потоком многих инструментов, и часто вы можете обнаружить два инструмента, которые кажутся коинтегрированными; но на самом деле они не коинтегрированы друг с другом, а коинтегрированы с рынок. Это называется искажающей переменной. Важно изучить участие рынка в любой найденной вами взаимосвязи.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Теперь попробуем найти коинтегрированные торговые пары, используя наш метод.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

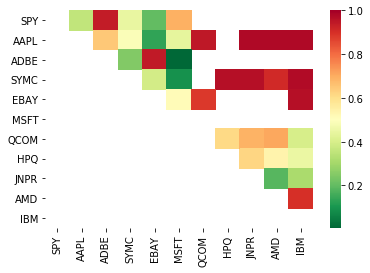
Похоже, что «ADBE» и «MSFT» коинтегрированы. Давайте посмотрим на цену, чтобы убедиться, что она действительно оправдана.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

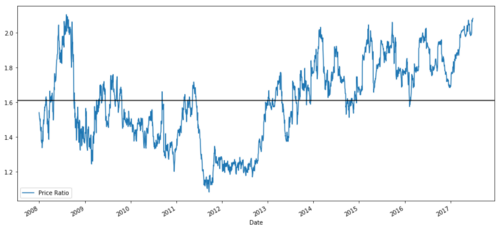
График соотношения цен MSFT и ADBE с 2008 по 2017 гг.

Это соотношение выглядит как стабильное среднее значение. Абсолютные коэффициенты не очень полезны в статистическом плане. Гораздо полезнее нормализовать наш сигнал, рассматривая его как z-оценку. Оценка Z определяется как:

Z Score (Value) = (Value — Mean) / Standard Deviation

предупреждать

На практике мы обычно пытаемся применить некоторое расширение к данным, но только если данные распределены нормально. Однако многие финансовые данные не имеют нормального распределения, поэтому мы должны быть очень осторожны и не предполагать нормальность или какое-либо конкретное распределение при формировании статистики. Истинное распределение коэффициентов может иметь толстые хвосты, а данные, которые стремятся к крайностям, могут запутать нашу модель и привести к огромным потерям.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

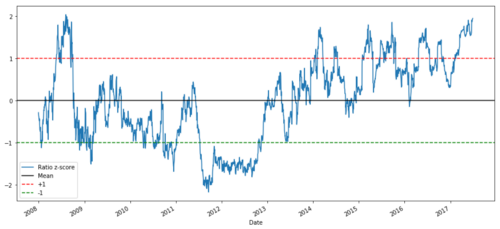
Соотношение Z-Price между MSFT и ADBE с 2008 по 2017 гг.

Теперь легче увидеть, как соотношение движется вокруг среднего значения, но иногда оно имеет тенденцию к большим отклонениям от среднего значения, что мы можем использовать.

Теперь, когда мы обсудили основы стратегии парной торговли и определили цели коинтеграции на основе истории цен, давайте попробуем разработать торговый сигнал. Сначала давайте рассмотрим шаги по разработке торговых сигналов с использованием методов обработки данных:

• Сбор надежных данных и очистка данных

• Создание функций из данных для определения торговых сигналов/логики

• В качестве признаков могут выступать скользящие средние значения или ценовые данные, корреляции или соотношения более сложных сигналов — объединяйте их для создания новых признаков.

• Используйте эти функции для генерации торговых сигналов, т. е. сигналов на покупку, продажу или короткие позиции.

К счастью, у нас есть Inventor Quantitative Platform (fmz.com), которая позволяет нам выполнить четыре вышеуказанных аспекта. Это большое благословение для разработчиков стратегии. Мы можем тратить свою энергию и время на логику стратегии, дизайн и функциональное расширение.

На платформе Inventor Quantitative Platform есть упакованные интерфейсы различных основных бирж. Все, что нам нужно сделать, это вызвать эти интерфейсы API. Остальная часть базовой логики реализации была отполирована профессиональной командой.

Для логической полноты и объяснения принципов мы подробно представим эти базовые логические схемы, но в реальной работе читатели могут напрямую вызывать интерфейс API Inventor Quant, чтобы завершить вышеуказанные четыре аспекта.

Давайте начнем:

Шаг 1: Определите проблему

Здесь мы пытаемся создать сигнал, который сообщает нам, будет ли отношение покупать или продавать в следующий момент, что является нашей предикторной переменной Y:

Y = Ratio is buy (1) or sell (-1)

Y(t)= Sign(Ratio(t+1) — Ratio(t))

Обратите внимание, что нам не нужно предсказывать фактическую цену базового актива или даже фактическое значение коэффициента (хотя мы можем это сделать), нам просто нужно предсказать направление коэффициента в дальнейшем.

Шаг 2: Соберите надежные и точные данные

Изобретатель Квант — ваш друг! Вы просто указываете инструменты, которыми хотите торговать, и источник данных, который хотите использовать, и система извлечет необходимые данные и очистит их для распределения дивидендов и инструментов. Итак, наши данные здесь уже очень чистые.

Мы использовали следующие данные Yahoo Finance по торговым дням за последние 10 лет (приблизительно 2500 точек данных): открытие, закрытие, максимум, минимум и объем.

Шаг 3: Разделение данных

Не забывайте об этом очень важном шаге проверки точности вашей модели. Мы используем следующее разделение данных на обучение/проверку/тестирование:

• Training 7 years ~ 70%

• Test ~ 3 years 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

В идеале мы также хотели бы создать проверочный набор, но сейчас мы этого делать не будем.

Шаг 4: Разработка функций

Каковы могут быть связанные функции? Мы хотим предсказать направление изменения соотношения. Мы увидели, что наши два инструмента коинтегрированы, поэтому это соотношение будет иметь тенденцию смещаться и возвращаться к среднему значению. Похоже, что наша функция должна быть некой мерой среднего значения отношения, а разница между текущим значением и средним может генерировать наш торговый сигнал.

Мы используем следующие функции:

• Коэффициент 60-дневной скользящей средней: мера скользящей средней

• Коэффициент 5-дневной скользящей средней: мера текущего значения средней

• 60-дневное стандартное отклонение

• z-оценка: (5d MA - 60d MA) / 60d SD

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

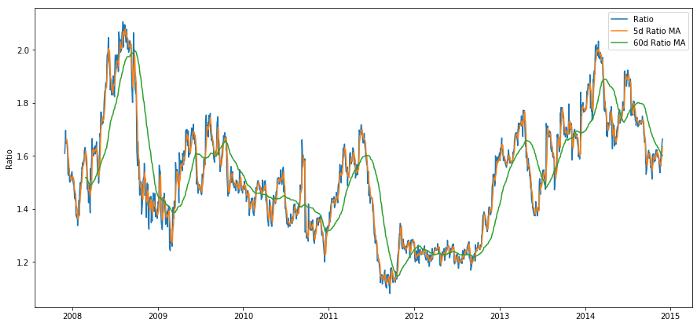
Соотношение цен 60d и 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

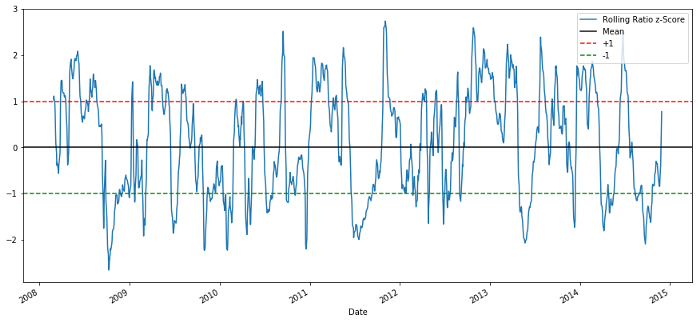
60-5 Z-оценка Соотношение цен

Z-оценка скользящего среднего действительно выявляет возвратную к среднему природу соотношения!

Шаг 5: Выбор модели

Начнем с очень простой модели. Глядя на график z-оценки, мы видим, что всякий раз, когда z-оценка слишком высокая или слишком низкая, она регрессирует. Давайте используем +1/-1 в качестве пороговых значений для определения слишком высокого и слишком низкого уровня, после чего мы сможем использовать следующую модель для генерации торговых сигналов:

• Когда z ниже -1,0, отношение равно покупателю (1), поскольку мы ожидаем, что z вернется к 0, поэтому отношение увеличивается.

• Когда z выше 1,0, коэффициент равен продаже (-1), поскольку мы ожидаем, что z вернется к 0, тем самым уменьшая коэффициент.

Шаг 6: Обучение, проверка и оптимизация

Наконец, давайте посмотрим, как на самом деле влияет наша модель на реальные данные? Давайте посмотрим, как этот сигнал ведет себя в реальных соотношениях.

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

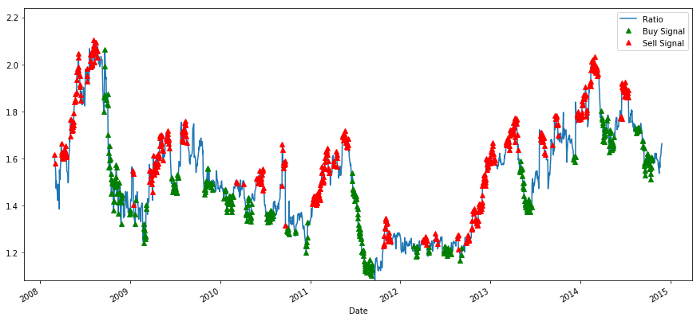
Сигналы соотношения цен покупки и продажи

Этот сигнал кажется разумным: мы продаем, когда коэффициент высок или растет (красные точки), и выкупаем, когда он низок (зеленые точки) и снижается. Что это означает для фактического предмета наших сделок? Давайте посмотрим

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

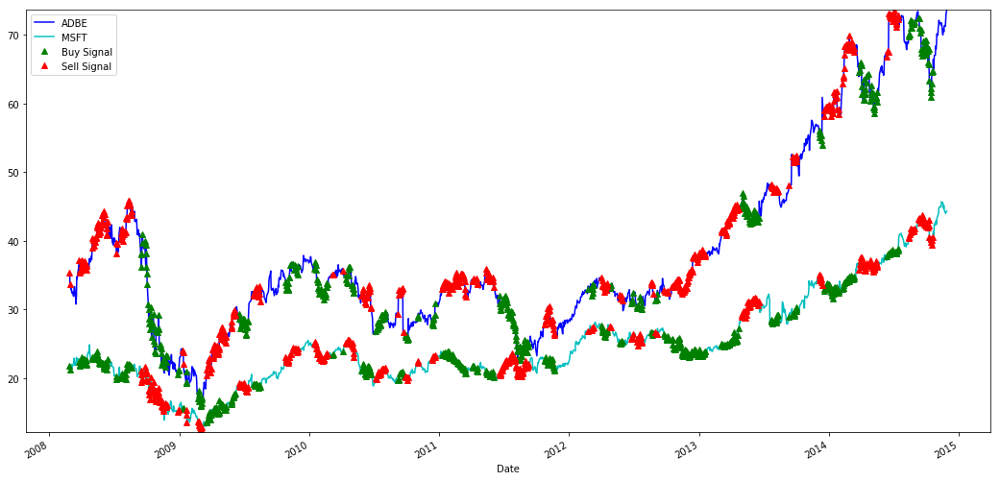
Сигналы на покупку и продажу акций MSFT и ADBE

Обратите внимание, как иногда мы зарабатываем деньги на «короткой ноге», иногда на «длинной ноге», а иногда и на обеих.

Мы довольны сигналом обучающих данных. Давайте посмотрим, какую прибыль может принести этот сигнал. Мы можем создать простой бэктестер, который покупает 1 отношение (покупает 1 акцию ADBE и продает отношение x акция MSFT), когда отношение низкое, и продает 1 отношение (продает 1 акцию ADBE и отношение колл x акция MSFT) и вычисляет PnL для этих сделок. соотношения.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Результат: 1783.375

Так что эта стратегия, похоже, прибыльна! Теперь мы можем провести дополнительную оптимизацию, изменив временное окно скользящей средней, изменив пороговые значения для покупки/продажи и закрытия позиций и т. д., а также проверить улучшение производительности на проверочных данных.

Мы также можем попробовать более сложные модели, такие как логистическая регрессия, SVM и т. д. для прогнозов 1/-1.

Теперь давайте продолжим эту модель, которая приводит нас к

Шаг 7: Проведите бэктест тестовых данных

Здесь я хотел бы упомянуть Inventor Quantitative Platform. Она использует высокопроизводительный движок бэктестинга QPS/TPS для истинного воспроизведения исторической среды, устранения распространенных ловушек количественного бэктестинга и оперативного обнаружения недостатков стратегии, чтобы лучше предоставлять реальные -время инвестиции. Предложите помощь.

Чтобы объяснить принцип, эта статья решила показать лежащую в основе логику. В практическом применении читателям рекомендуется использовать Inventor Quantitative Platform. Помимо экономии времени, важно улучшить показатель отказоустойчивости.

Бэктестинг прост. Мы можем использовать указанную выше функцию для просмотра PnL тестовых данных.

trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)

Результат: 5262.868

Эта модель очень хорошо сделана! Это стала нашей первой простой моделью парной торговли.

Избегайте переобучения

Прежде чем закончить, я хотел бы поговорить конкретно о переобучении. Переобучение — самая опасная ловушка в торговых стратегиях. Алгоритм переобучения может работать очень хорошо при бэктестинге, но не работать на новых, ранее неизвестных данных. Это означает, что он на самом деле не выявляет никаких тенденций в данных и не имеет реальной предсказательной силы. Давайте рассмотрим простой пример.

В нашей модели мы используем скользящие оценки параметров и надеемся оптимизировать длину временного окна. Мы можем решить просто перебрать все возможности, разумные длины временных окон и выбрать тот временной интервал, при котором наша модель работает лучше всего. Ниже мы напишем простой цикл для оценки длин временных окон на основе PNL обучающих данных и найдем лучший цикл.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Теперь мы проверяем работу модели на тестовых данных и видим, что эта длина временного окна далека от оптимальной! Это связано с тем, что наш первоначальный выбор явно не соответствует данным выборки.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Очевидно, что то, что хорошо работает для наших выборочных данных, не всегда дает хорошие результаты в будущем. Для проверки давайте построим график оценок длины, рассчитанных на основе двух наборов данных.

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

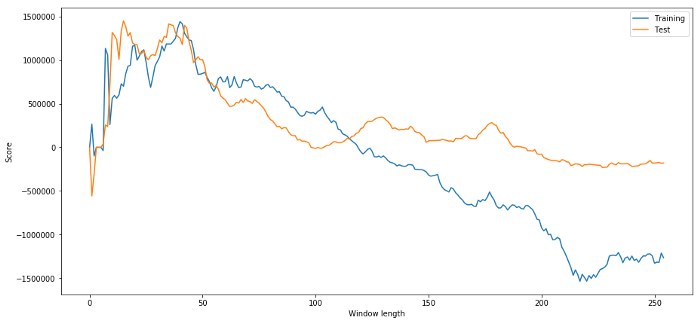
Мы видим, что любой диапазон от 20 до 50 является хорошим выбором для временного окна.

Чтобы избежать переобучения, мы можем использовать экономические соображения или свойства алгоритма для выбора длины временного окна. Мы также можем использовать фильтр Калмана, который не требует указания длины; этот метод будет рассмотрен позже в другой статье.

Следующий шаг

В этой статье мы представляем несколько простых вводных методов, демонстрирующих процесс разработки торговой стратегии. На практике следует использовать более сложную статистику, и вы можете рассмотреть следующие варианты:

• показатель Херста

• Период полураспада среднего возврата, выведенный из процесса Орнштейна-Уленбека

• фильтр Калмана