سپائی اور آئی ڈبلیو ایم کے مابین ایک انٹرا ڈے میڈین ریورس جوڑی کی حکمت عملی کا بیک ٹیسٹنگ

اس مضمون میں ہم اپنی پہلی انٹرا ڈے ٹریڈنگ حکمت عملی پر غور کرنے جارہے ہیں۔ یہ ایک کلاسیکی ٹریڈنگ آئیڈیا ، ٹریڈنگ جوڑے کا استعمال کرے گا۔ اس معاملے میں ہم دو ایکسچینج ٹریڈڈ فنڈز (ای ٹی ایف) ، ایس پی وائی اور آئی ڈبلیو ایم کا استعمال کرنے جارہے ہیں ، جو نیو یارک اسٹاک ایکسچینج (این وائی ایس ای) میں تجارت کرتے ہیں اور بالترتیب امریکی اسٹاک مارکیٹ انڈیکس ، ایس اینڈ پی 500 اور رسل 2000 کی نمائندگی کرنے کی کوشش کرتے ہیں۔

یہ حکمت عملی وسیع پیمانے پر ای ٹی ایف کے جوڑے کے مابین پھیلاؤ پیدا کرتی ہے جس میں ایک کو لمبا اور دوسرے کی رقم کو مختصر کردیا جاتا ہے۔ لمبے عرصے سے مختصر کا تناسب بہت سارے طریقوں سے بیان کیا جاسکتا ہے جیسے شماریاتی کو انٹیگریٹنگ ٹائم سیریز کی تکنیکوں کا استعمال کرتے ہوئے۔ اس منظر نامے میں ہم رولنگ لکیری رجسٹریشن کے ذریعہ ایس پی وائی اور آئی ڈبلیو ایم کے مابین ہیج تناسب کا حساب لگائیں گے۔ اس کے بعد ہم ایس پی وائی اور آئی ڈبلیو ایم کے مابین پھیلاؤ پیدا کرنے کی اجازت دیں گے جو زیڈ اسکور تک معمول پر ہے۔ جب زیڈ اسکور کچھ حد سے تجاوز کرتا ہے تو تجارتی سگنل پیدا ہوجائیں گے اس یقین کے تحت کہ پھیلاؤ اوسط تک واپس آجائے گا۔

اس حکمت عملی کی دلیل یہ ہے کہ ایس پی وائی اور آئی ڈبلیو ایم تقریبا ایک ہی صورتحال کی خصوصیت رکھتے ہیں ، جو بڑی اور چھوٹی سرمایہ کاری والی امریکی کارپوریشنوں کے ایک گروپ کی معیشت کی ہے۔ اس کا فرض یہ ہے کہ اگر کسی نے قیمتوں کا پھیلاؤ لیا تو اس کا مطلب یہ ہونا چاہئے کہ ، جبکہ مقامی (وقت میں) واقعات یا تو ایس اینڈ پی 500 یا رسل 2000 اشاریہ جات کو الگ الگ متاثر کرسکتے ہیں (جیسے چھوٹی سرمایہ کاری / بڑی سرمایہ کاری کے اختلافات ، دوبارہ توازن کی تاریخیں یا بلاک تجارت) ، دونوں کی طویل مدتی قیمتوں کی سیریز کو ممکنہ طور پر مربوط کیا جائے گا۔

حکمت عملی

اسٹریٹیجی کو مندرجہ ذیل مراحل میں لاگو کیا جاتا ہے:

1. اعداد و شمار - ایس پی وائی اور آئی ڈبلیو ایم کے 1 منٹ کے بار اپریل 2007 سے فروری 2014 تک حاصل کیے گئے ہیں۔
2. پروسیسنگ - اعداد و شمار کو درست طریقے سے سیدھ کیا جاتا ہے اور لاپتہ سلاخوں کو باہمی طور پر خارج کردیا جاتا ہے۔
3. پھیلاؤ - دو ای ٹی ایف کے مابین ہیج تناسب کا حساب رولنگ لکیری رجسٹریشن لے کر کیا جاتا ہے۔ اس کی وضاحت بیک بیک ونڈو کا استعمال کرتے ہوئے β رجسٹریشن کوفیکٹر کے طور پر کی جاتی ہے جو 1 بار آگے بڑھتا ہے اور رجسٹریشن کوفیکٹرز کا دوبارہ حساب لگاتا ہے۔ اس طرح ، بیک بی کے لئے ہیج تناسب βi ، k باروں کے بیک بیک کے لئے نکات bi−1−k سے bi−1 کے درمیان حساب کیا جاتا ہے۔
4. زیڈ اسکور - پھیلاؤ کا معیاری اسکور معمول کے مطابق حساب کیا جاتا ہے۔ اس کا مطلب ہے کہ پھیلاؤ کے (نمونے) اوسط کو گھٹانا اور پھیلاؤ کے (نمونے) معیاری انحراف سے تقسیم کرنا۔ اس کی وجہ یہ ہے کہ حد کے پیرامیٹرز کو زیادہ سیدھے سیدھے کرنے کے ل since چونکہ زیڈ اسکور ایک جہتی مقدار ہے ۔ میں نے جان بوجھ کر حساب کتاب میں ایک لوک ہیڈ تعصب متعارف کرایا ہے تاکہ یہ ظاہر کیا جاسکے کہ یہ کتنا ٹھیک ہوسکتا ہے۔ کوشش کریں اور اس پر نظر رکھیں!
5. تجارت - جب منفی زیڈ اسکور پہلے سے طے شدہ (یا پوسٹ آپٹمائزڈ) حد سے نیچے آجاتا ہے تو لانگ سگنل پیدا ہوتے ہیں ، جبکہ مختصر سگنل اس کے برعکس ہوتے ہیں۔ جب مطلق زیڈ اسکور ایک اضافی حد سے نیچے آجاتا ہے تو باہر نکلنے کے سگنل پیدا ہوتے ہیں۔ اس حکمت عملی کے ل I میں نے (کچھ حد تک اپنی مرضی سے) ایک مطلق اندراج کی حد منتخب کی ہے۔

شاید حکمت عملی کو گہرائی سے سمجھنے کا بہترین طریقہ یہ ہے کہ اسے واقعتا implement اس پر عمل درآمد کریں۔ مندرجہ ذیل حصے میں اس اوسط ریورسنگ حکمت عملی کو نافذ کرنے کے لئے ایک مکمل پائتھون کوڈ (واحد فائل) کی وضاحت کی گئی ہے۔ میں نے سمجھنے میں مدد کے لئے کوڈ پر آزادانہ طور پر تبصرہ کیا ہے۔

پائیتھون کا نفاذ

جیسا کہ تمام پائتھون / پانڈاس سبق کے ساتھ ضروری ہے کہ اس سبق میں بیان کردہ پائتھون ریسرچ ماحول کو ترتیب دیا جائے۔ ایک بار انسٹال ہونے کے بعد ، پہلا کام ضروری پائتھون لائبریریوں کو درآمد کرنا ہے۔ اس بیک ٹیسٹ کے لئے میٹ پلٹلب اور پانڈاس کی ضرورت ہے۔

مخصوص لائبریری ورژن جو میں استعمال کر رہا ہوں مندرجہ ذیل ہیں:

• پائیتھون - 2.7.3
• NumPy - 1.8.0
• پانڈا - 0.12.0
• میٹپلوٹلیب - 1.1.0 آئیے آگے بڑھیں اور لائبریریاں درآمد کریں:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

مندرجہ ذیل فنکشن create_pairs_dataframe دو علامتوں کی انٹرا ڈے باروں پر مشتمل دو CSV فائلوں کو درآمد کرتا ہے۔ ہمارے معاملے میں یہ SPY اور IWM ہوگا۔ اس کے بعد یہ ایک علیحدہ ڈیٹا فریم جوڑا بناتا ہے ، جو دونوں اصل فائلوں کے اشاریہ جات کا استعمال کرتا ہے۔ چونکہ ان کے ٹائم اسٹیمپ کو یاد آنے والی تجارتوں اور غلطیوں کی وجہ سے مختلف ہونے کا امکان ہے ، اس سے یہ یقینی بنتا ہے کہ ہمارے پاس مماثل ڈیٹا ہوگا۔ یہ پانڈا جیسے ڈیٹا تجزیہ لائبریری کا استعمال کرنے کا ایک اہم فائدہ ہے۔ boilerplate کوڈ ہمارے لئے بہت موثر انداز میں سنبھالا جاتا ہے۔

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

اگلے مرحلے میں ایس پی وائی اور آئی ڈبلیو ایم کے مابین رولنگ لکیری رجسٹریشن انجام دینا ہے۔ اس مثال میں آئی ڈبلیو ایم پیش گوئی کرنے والا ( ایکس) ہے اور ایس پی وائی جواب ( وائی) ہے۔ میں نے 100 بار کی ڈیفالٹ لوک بیک ونڈو مرتب کی ہے۔ جیسا کہ اوپر بیان کیا گیا ہے ، یہ حکمت عملی کا ایک پیرامیٹر ہے۔ حکمت عملی کو مضبوط سمجھنے کے ل we ہم مثالی طور پر واپسی کا پروفائل (یا کارکردگی کی دیگر پیمائش) کو لوک بیک مدت کے convex فنکشن کے طور پر دیکھنا چاہتے ہیں۔ اس طرح کوڈ کے بعد کے مرحلے میں ہم کسی حد تک لوک بیک مدت کو مختلف کرکے حساسیت کا تجزیہ کریں گے۔

ایک بار جب SPY-IWM کے ل the لکیری رجعت ماڈل میں رولنگ بیٹا کوفیسیئنٹ کا حساب لگایا جاتا ہے تو ، ہم اسے جوڑوں ڈیٹا فریم میں شامل کرتے ہیں اور خالی قطاروں کو چھوڑ دیتے ہیں۔ یہ ٹرمنگ پیمائش کے طور پر نظرثانی کے سائز کے برابر سلاخوں کا پہلا سیٹ تشکیل دیتا ہے۔ اس کے بعد ہم دو ETFs کا پھیلاؤ SPY اور IWM کی −βi اکائیوں کی اکائی کے طور پر بناتے ہیں۔ واضح طور پر یہ حقیقت پسندانہ صورتحال نہیں ہے کیونکہ ہم IWM کی جزوی مقدار لے رہے ہیں ، جو حقیقی نفاذ میں ممکن نہیں ہے۔

آخر میں ، ہم پھیلاؤ کا زیڈ اسکور بناتے ہیں ، جس کا حساب پھیلاؤ کے اوسط کو گھٹاتے ہوئے اور پھیلاؤ کے معیاری انحراف سے معمول پر لاتے ہوئے کیا جاتا ہے۔ نوٹ کریں کہ یہاں ایک بہت ہی ٹھیک ٹھیک نظر آنے والا تعصب واقع ہوتا ہے۔ میں نے اسے کوڈ میں جان بوجھ کر چھوڑ دیا کیونکہ میں اس بات پر زور دینا چاہتا تھا کہ تحقیق میں ایسی غلطی کرنا کتنا آسان ہے۔ اوسط اور معیاری انحراف پورے پھیلاؤ کے وقت کی سیریز کے لئے حساب کیا جاتا ہے۔ اگر یہ حقیقی تاریخی درستگی کی عکاسی کرنا ہے تو پھر یہ معلومات دستیاب نہیں ہوں گی کیونکہ یہ ضمنی طور پر مستقبل کی معلومات کا استعمال کرتی ہے۔ لہذا ہمیں رولنگ میڈین اور اسٹڈیو کا استعمال کرنا چاہئے تاکہ زیڈ اسکور کا حساب لگایا جاسکے۔

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

create_long_short_market_signals میں تجارتی سگنل بنائے جاتے ہیں۔ ان کا حساب اس وقت لگایا جاتا ہے جب زیڈ اسکور منفی زیڈ اسکور سے منفی حد تک بڑھ جاتا ہے اور جب زیڈ اسکور مثبت زیڈ اسکور سے زیادہ ہوتا ہے تو پھیلاؤ طویل ہوجاتا ہے اور جب زیڈ اسکور مثبت زیڈ اسکور سے زیادہ ہوجاتا ہے تو پھیلاؤ مختصر ہوجاتا ہے۔ جب زیڈ اسکور کی مطلق قیمت کسی اور (تعداد میں چھوٹی) حد سے کم یا مساوی ہوتی ہے تو ایگزٹ سگنل دیا جاتا ہے۔

اس صورتحال کو حاصل کرنے کے لئے یہ جاننا ضروری ہے کہ ہر بار کے لئے ، حکمت عملی مارکیٹ میں ہے یا باہر ہے۔ لانگ_مارکیٹ اور شارٹ_مارکیٹ دو متغیر ہیں جو مارکیٹ کی لمبی اور مختصر پوزیشنوں کا سراغ لگانے کے لئے بیان کیے گئے ہیں۔ بدقسمتی سے یہ ویکٹرائزڈ نقطہ نظر کے برعکس تکرار کے انداز میں کوڈ کرنے میں بہت آسان ہے اور اس طرح اس کا حساب لگانا سست ہے۔ 1 منٹ کی سلاخوں کے باوجود جس میں ہر CSV فائل کے لئے ~ 700،000 ڈیٹا پوائنٹس کی ضرورت ہوتی ہے ، یہ اب بھی میری پرانی ڈیسک ٹاپ مشین پر حساب کتاب کرنا نسبتا fast تیز ہے!

پانڈا ڈیٹا فریم پر تکرار کرنے کے لئے (جو تسلیم شدہ طور پر ایک عام آپریشن نہیں ہے) یہ iterrows طریقہ استعمال کرنا ضروری ہے ، جو ایک جنریٹر فراہم کرتا ہے جس پر تکرار کرنا ہے:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

اس مرحلے میں ہم نے اصل طویل / مختصر سگنل پر مشتمل جوڑوں کو اپ ڈیٹ کیا ہے ، جس سے ہمیں یہ طے کرنے کی اجازت ملتی ہے کہ ہمیں مارکیٹ میں ہونے کی ضرورت ہے یا نہیں۔ اب ہمیں پوزیشنوں کی مارکیٹ ویلیو کا سراغ لگانے کے لئے ایک پورٹ فولیو بنانے کی ضرورت ہے۔ پہلا کام پوزیشنوں کا ایک کالم بنانا ہے جو طویل اور مختصر سگنل کو جوڑتا ہے۔ اس میں (1,0,−1) سے عناصر کی ایک فہرست ہوگی ، جس میں 1 طویل / مارکیٹ پوزیشن کی نمائندگی کرتا ہے ، 0 کوئی پوزیشن کی نمائندگی نہیں کرتا ہے (خرید ہونا چاہئے) اور -1 مختصر / مارکیٹ پوزیشن کی نمائندگی کرتا ہے۔ sym1 اور sym2 کالم ہر بار کے اختتام پر SPY اور IWM پوزیشنوں کی مارکیٹ اقدار کی نمائندگی کرتے ہیں۔

ایک بار جب ای ٹی ایف مارکیٹ کی قیمتیں بن جاتی ہیں تو ، ہم ان کو جمع کرتے ہیں تاکہ ہر بار کے اختتام پر ایک کل مارکیٹ ویلیو تیار کیا جاسکے۔ اس کے بعد اس سیریز آبجیکٹ کے لئے pct_change طریقہ کار کے ذریعہ واپسی کے سلسلے میں تبدیل ہوجاتا ہے۔ کوڈ کی بعد کی لائنیں خراب اندراجات (NaN اور inf عناصر) کو صاف کرتی ہیں اور آخر میں مکمل ایکویٹی وکر کا حساب لگاتی ہیں۔

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

کےاہمآپ کے ڈیٹا ڈائرکٹری میں موجود تمام فائلوں کو ایک دوسرے کے ساتھ جوڑتا ہے۔ انٹرا ڈے CSV فائلیں ڈیٹا ڈائرکٹری کے راستے پر واقع ہیں۔ ذیل میں موجود کوڈ کو اپنی مخصوص ڈائرکٹری کی طرف اشارہ کرنے کے لئے تبدیل کرنا یقینی بنائیں۔

اس بات کا تعین کرنے کے لئے کہ حکمت عملی نظرثانی کی مدت کے لئے کس طرح حساس ہے ، نظرثانیوں کی ایک حد کے لئے کارکردگی کی پیمائش کا حساب لگانا ضروری ہے۔ میں نے کارکردگی کی پیمائش کے طور پر پورٹ فولیو کی حتمی کل فیصد واپسی اور نظرثانی کی حد کو [50,200] میں 10 کے اضافے کے ساتھ منتخب کیا ہے۔ آپ مندرجہ ذیل کوڈ میں دیکھ سکتے ہیں کہ پچھلے افعال کو اس حد میں ایک لوپ میں لپیٹ دیا گیا ہے ، جس میں دیگر حدیں طے شدہ ہیں۔ حتمی کام یہ ہے کہ میٹ پلٹ لیب کا استعمال کرکے نظرثانیوں کے مقابلے میں واپسی کا لائن چارٹ بنائیں:

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

لوک بیک مدت بمقابلہ واپسی کا چارٹ اب دیکھا جاسکتا ہے۔ نوٹ کریں کہ لوک بیک کے ارد گرد 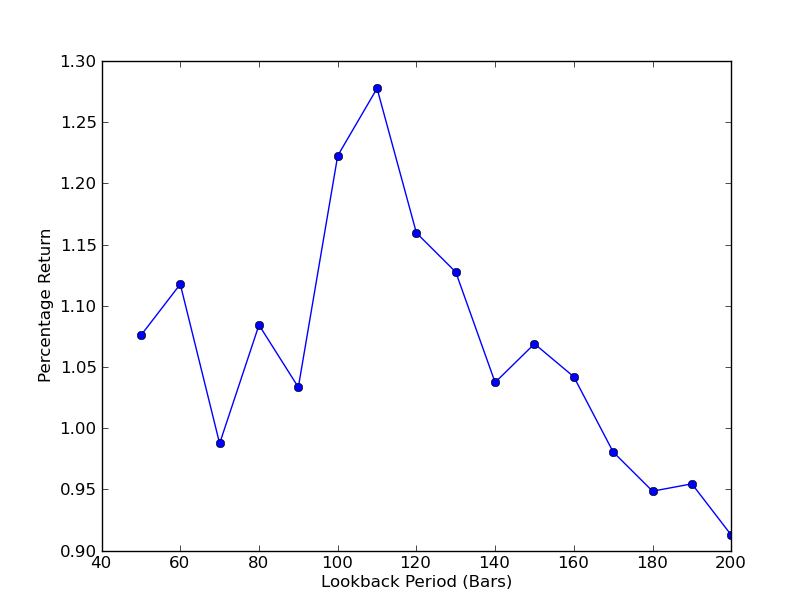global زیادہ سے زیادہ 110 بار کے برابر ہے۔ اگر ہم نے ایسی صورتحال دیکھی ہوتی جہاں لوک بیک واپسی سے آزاد ہوتا تو یہ تشویش کا باعث ہوتا:SPY-IWM لکیری رجسٹریشن ہیج ریشو بیک بیک پیریڈ حساسیت تجزیہ

بیک ٹسٹنگ کا کوئی مضمون اوپر کی طرف جھکنے والے ایکویٹی منحنی خطوط کے بغیر مکمل نہیں ہوگا! لہذا اگر آپ وقت کے مقابلے میں مجموعی منافع کا منحنی خطوط بنانا چاہتے ہیں تو ، آپ مندرجہ ذیل کوڈ استعمال کرسکتے ہیں۔ یہ لوک بیک پیرامیٹر اسٹڈی سے تیار کردہ حتمی پورٹ فولیو کو پلاٹ کرے گا۔ اس طرح آپ کو اس بات پر منحصر ہے کہ آپ کس چارٹ کو دیکھنا چاہتے ہیں۔ چارٹ میں موازنہ میں مدد کے لئے اسی مدت میں ایس پی وائی کی واپسی کو بھی پلاٹ کیا گیا ہے:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

مندرجہ ذیل ایکویٹی وکر کا چارٹ 100 دن کی بیک بیک مدت کے لئے ہے: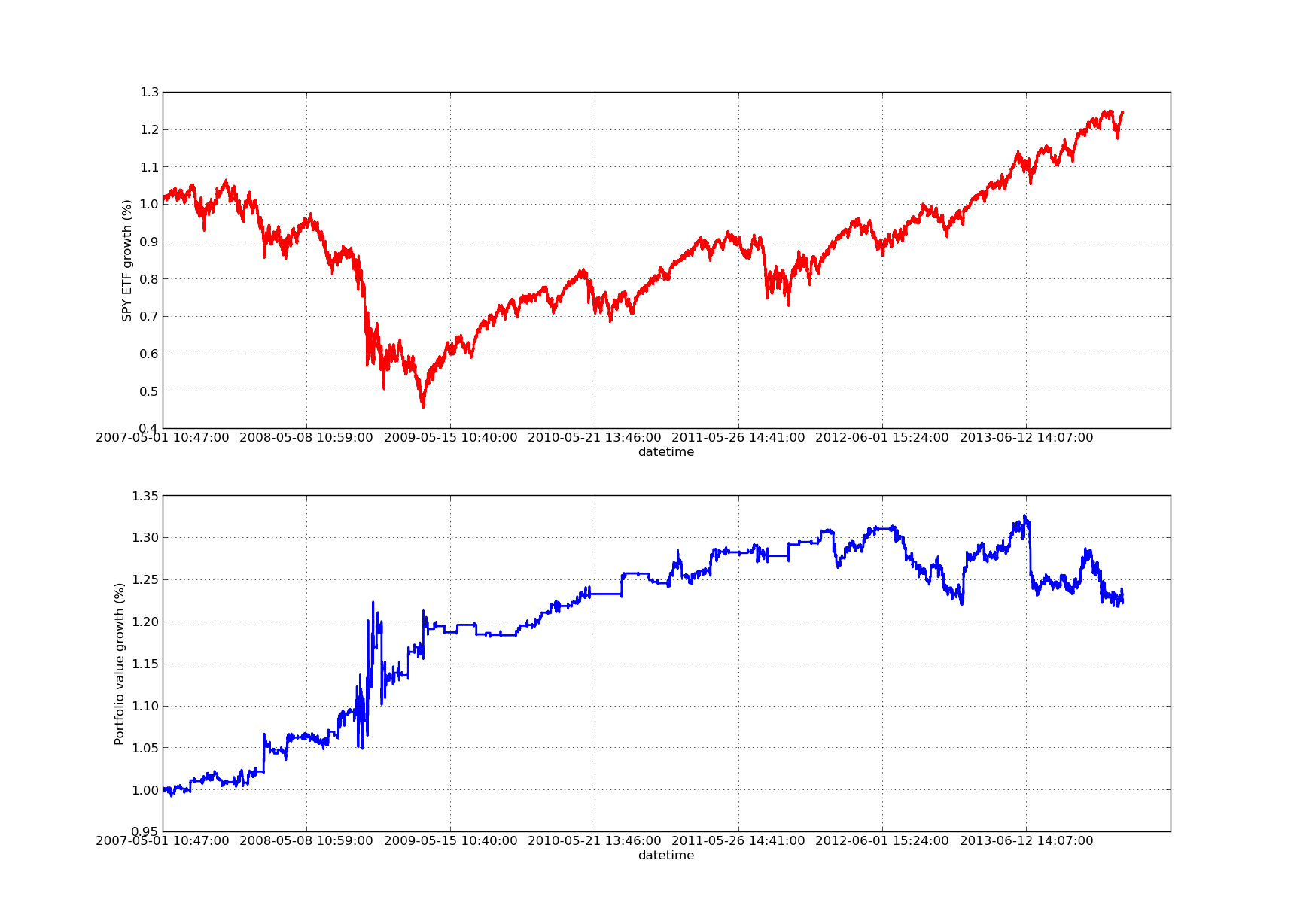SPY-IWM لکیری رجسٹریشن ہیج ریشو بیک بیک پیریڈ حساسیت تجزیہ

نوٹ کریں کہ مالیاتی بحران کے دوران 2009 میں ایس پی وائی کی کھپت میں نمایاں کمی واقع ہوئی ہے۔ اس مرحلے میں اس حکمت عملی میں بھی اتار چڑھاؤ کا دور تھا۔ یہ بھی نوٹ کریں کہ اس عرصے میں ایس پی وائی کی مضبوط رجحان کی نوعیت کی وجہ سے گذشتہ سال کارکردگی میں کچھ حد تک خرابی واقع ہوئی ہے ، جو ایس اینڈ پی 500 انڈیکس کی عکاسی کرتی ہے۔

نوٹ کریں کہ اسپریڈ کے زیڈ اسکور کا حساب لگاتے وقت ہمیں اب بھی لوک ہیڈ تعصب کو مدنظر رکھنا ہوگا۔ مزید برآں ، یہ تمام حساب کتاب لین دین کے اخراجات کے بغیر کیے گئے ہیں۔ یہ حکمت عملی یقینی طور پر ان عوامل کو مدنظر رکھتے ہوئے بہت خراب کارکردگی کا مظاہرہ کرے گی۔ فیس ، بولی / پوچھنے کا پھیلاؤ اور سلائپج فی الحال سبھی کا حساب نہیں لیا جاتا ہے۔ اس کے علاوہ حکمت عملی ای ٹی ایف کی جزوی اکائیوں میں تجارت کر رہی ہے ، جو بھی بہت غیر حقیقت پسندانہ ہے۔

بعد کے مضامین میں ہم ایک بہت زیادہ نفیس واقعہ سے چلنے والی بیک ٹیسٹر بنائیں گے جو ان عوامل کو مدنظر رکھے گا اور ہمیں اپنے ایکویٹی وکر اور کارکردگی کے معیار میں نمایاں طور پر زیادہ اعتماد فراہم کرے گا۔