Bayesian statistics ریاضی کا ایک طاقتور ڈسپلن ہے جس میں مالیات، طبی تحقیق، اور انفارمیشن ٹیکنالوجی سمیت کئی شعبوں میں وسیع اطلاقات ہیں۔ یہ ہمیں نئے بعد کے عقائد تک پہنچنے کے لیے ثبوت کے ساتھ سابقہ ​​عقائد کو یکجا کرنے کی اجازت دیتا ہے، جس سے ہمیں مزید باخبر فیصلے کرنے کی اجازت ملتی ہے۔

اس مضمون میں، ہم مختصراً چند اہم ریاضی دانوں کا تعارف کرائیں گے جنہوں نے اس شعبے کی بنیاد رکھی۔

Bayes سے پہلے Bayesian اعداد و شمار کو بہتر طور پر سمجھنے کے لیے، ہمیں 18ویں صدی میں واپس جانے کی ضرورت ہے اور ریاضی دان De Moivre اور اس کے مقالے “The Principle of Chance” کا حوالہ دینا ہوگا۔[1]。

اپنے مقالے میں، De Moivre نے امکان اور جوئے سے متعلق اپنے وقت کے بہت سے مسائل کو حل کیا۔ جیسا کہ آپ شاید جانتے ہوں گے، ان میں سے کسی ایک مسئلے کے حل نے عام تقسیم کی ابتدا کی، لیکن یہ ایک اور کہانی ہے۔

اس کے مقالے میں ایک سادہ سا سوال ہے:

“ایک منصفانہ سکے کو لگاتار تین بار اچھالنے پر تین سر ملنے کا امکان۔”

“موقع کے اصول” میں بیان کردہ مسائل کو پڑھتے ہوئے آپ محسوس کر سکتے ہیں کہ ان میں سے اکثر کا آغاز ایک مفروضے سے ہوتا ہے جس سے کسی واقعہ کے امکان کا حساب لگایا جاتا ہے۔ مثال کے طور پر، مندرجہ بالا مسئلہ میں، ایک مفروضہ ہے کہ سکہ منصفانہ ہے، اس لیے ٹاس میں سر ملنے کا امکان 0.5 ہے۔

اس کا اظہار آج ریاضی کی اصطلاح میں اس طرح کیا جاتا ہے:

𝑃(𝑋|𝜃)

لیکن کیا ہوگا اگر ہم نہیں جانتے کہ سکہ منصفانہ ہے یا نہیں؟ اگر ہم نہیں جانتے𝜃اونی کپڑا۔

تھامس بیز اور رچرڈ پرائس

تقریباً پچاس سال بعد، 1763 میں، “موقع کے اصول پر ایک مضمون” کے عنوان سے ایک مقالہ آیا۔[2] رائل سوسائٹی آف لندن کے فلسفیانہ لین دین میں شائع ہوا۔

دستاویز کے ابتدائی چند صفحات میں ریاضی دان رچرڈ پرائس کی تحریر کردہ تحریر ہے، جس میں اس کے دوست تھامس بیز کی موت سے چند سال قبل لکھے گئے ایک مقالے کا خلاصہ ہے۔ تعارف میں، پرائس تھامس بیز کی طرف سے کی گئی کچھ دریافتوں کی اہمیت کی وضاحت کرتا ہے جو ڈی موویرے کے پرنسپلز آف چانس میں شامل نہیں تھیں۔

درحقیقت وہ ایک خاص مسئلہ کی طرف اشارہ کر رہا تھا:

“کسی نامعلوم واقعے کے وقوع اور ناکامیوں کی تعداد کو دیکھتے ہوئے، امکان کی کسی بھی دو نامزد ڈگریوں کے درمیان اس کے وقوع پذیر ہونے کا امکان تلاش کریں۔”

دوسرے لفظوں میں، ایک واقعہ کا مشاہدہ کرنے کے بعد، ہمیں نامعلوم پیرامیٹر ملتا ہے۔θدو امکانی ڈگریوں کے درمیان کیا امکان ہے؟ یہ درحقیقت شماریاتی تخمینہ سے متعلق تاریخ کے اولین مسائل میں سے ایک ہے، اور اس نے نام الٹا امکان کو جنم دیا۔ ریاضی کے لحاظ سے:

𝑃( 𝜃 | 𝑋）

یقیناً یہ وہی ہے جسے آج ہم Bayes کے تھیوریم کی posterior distribution کہتے ہیں۔

بے سبب وجوہات

ان دو بزرگ پادریوں کو جانیں۔تھامس بیزاوررچرڈ پرائس، جس چیز نے تحقیق کی حوصلہ افزائی کی وہ دراصل بہت دلچسپ ہے۔ لیکن ایسا کرنے کے لیے، ہمیں ایک لمحے کے لیے اعداد و شمار کے بارے میں کچھ علم کو ایک طرف رکھنے کی ضرورت ہے۔

ہم 18ویں صدی میں ہیں، اور امکان ریاضی دانوں کی دلچسپی کا ایک شعبہ بنتا جا رہا ہے۔ De Moivre یا Bernoulli جیسے ریاضی دانوں نے دکھایا تھا کہ کچھ واقعات ایک خاص حد تک بے ترتیب پن کے ساتھ ہوتے ہیں لیکن پھر بھی مقررہ اصولوں کے تحت چلتے ہیں۔ مثال کے طور پر، اگر آپ کئی بار ڈائی رول کرتے ہیں، تو چھ میں سے ایک بار یہ چھکے پر اترے گا۔ یہ گویا ایک پوشیدہ اصول ہے جو موقع کی تقدیر کا تعین کرتا ہے۔

اب، تصور کریں کہ آپ اس دور میں رہنے والے ایک ریاضی دان اور ایک متقی مومن ہیں۔ آپ کو یہ جاننے میں دلچسپی ہو سکتی ہے کہ اس پوشیدہ اصول کا خدا سے کیا تعلق ہے۔

یہ واقعی وہ سوال ہے جو Bayes اور Price نے خود پوچھا تھا۔ انہوں نے اس مسئلے کو حل کرنے کی جس حل کی امید کی تھی وہ براہ راست یہ ثابت کرنے پر لاگو ہوتا تھا کہ “دنیا کو حکمت اور ذہانت کا نتیجہ ہونا چاہیے؛ اس طرح خدا کے وجود کو حتمی وجہ کے طور پر ثابت کرنا”[2] - یعنی کوئی وجہ اور اثر نہیں ہے۔

لاپلیس

حیرت کی بات یہ ہے کہ تقریباً دو سال بعد، 1774 میں، بظاہر تھامس بیز کا مقالہ پڑھے بغیر، فرانسیسی ریاضی دان لاپلاس نے “واقعات کے امکانات کے ذریعے واقعات کی وجوہات” کے عنوان سے ایک مقالہ لکھا[3]، جو الٹا امکان کے مسئلے پر ایک کاغذ ہے۔ پہلے صفحے پر آپ پڑھ سکتے ہیں۔

اہم اصول یہ ہیں:

“اگر کوئی واقعہ n مختلف وجوہات کی وجہ سے ہوسکتا ہے، تو کسی واقعہ کے لیے ان اسباب کے امکانات اس وجہ سے ہونے والے واقعے کے امکان کے برابر ہیں، اور ان وجوہات میں سے ہر ایک کے وجود کا امکان برابر ہے۔ وجہ دی گئی واقعہ کے امکان کو، ان وجوہات میں سے ہر ایک کو دیئے گئے واقعہ کے امکانات کے مجموعے سے تقسیم کیا جاتا ہے۔

یہ وہی ہے جسے ہم آج Bayes کے نظریہ کے طور پر جانتے ہیں:

​

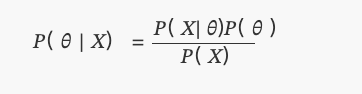
میںP(θ)یکساں طور پر تقسیم کیا جاتا ہے۔

سکے کا تجربہ

ہم Python اور PyMC لائبریری کا استعمال کرتے ہوئے اور ایک سادہ تجربہ کر کے Bayesian کے اعدادوشمار کو موجودہ میں لائیں گے۔

فرض کریں کہ ایک دوست آپ کو ایک سکہ دیتا ہے اور آپ سے پوچھتا ہے کہ کیا آپ کے خیال میں یہ ایک اچھا سکہ ہے۔ کیونکہ وہ جلدی میں ہے، وہ آپ سے کہتا ہے کہ سکے کو صرف 10 بار پلٹائیں۔ جیسا کہ آپ دیکھ سکتے ہیں، اس مسئلے میں ایک نامعلوم پیرامیٹر ہے۔p، سکے ٹاس میں سر حاصل کرنے کا امکان، اور ہم اس کا اندازہ لگانا چاہتے ہیں۔pکی سب سے زیادہ ممکنہ قیمت

(نوٹ: ہم پیرامیٹرز کے بارے میں بات نہیں کر رہے ہیں۔pایک بے ترتیب متغیر ہے، لیکن یہ پیرامیٹر طے شدہ ہے اور ہم جاننا چاہتے ہیں کہ کن اقدار کے درمیان اس کا زیادہ امکان ہے۔ )

اس مسئلے پر ایک مختلف نقطہ نظر حاصل کرنے کے لیے، ہم اسے دو مختلف پیشگی عقائد کے تحت حل کریں گے:

• 1. آپ کو سکے کے منصفانہ ہونے کے بارے میں کوئی پیشگی معلومات نہیں ہیں اور آپ کو مساوی امکانات تفویض کرتے ہیں۔p. اس صورت میں، ہم اسے استعمال کریں گے جسے غیر معلوماتی پیشگی کہا جاتا ہے، کیونکہ آپ اپنے عقیدے میں کوئی معلومات شامل نہیں کر رہے ہیں۔
• 1. آپ تجربے سے جانتے ہیں کہ اگر کوئی سکہ غیر منصفانہ ہو تو بھی اسے بہت غیر منصفانہ بنانا مشکل ہے، لہذا آپ کے خیال میں پیرامیٹرزpزیادہ امکان ہے کہ یہ 0.3 سے نیچے یا 0.7 سے اوپر نہیں جائے گا۔ اس صورت میں، ہم ایک معلوماتی پیشگی استعمال کریں گے۔

دونوں صورتوں کے لیے، ہمارے پیشگی عقائد حسب ذیل ہوں گے:

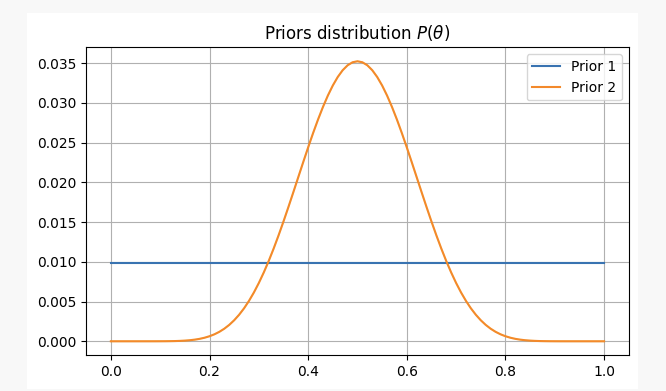
ایک سکے کو 10 بار اچھالنے کے بعد، آپ کو 2 سر ملتے ہیں۔ اس ثبوت کے ساتھ، ہم شاید یہ جان سکتے ہیں کہ ہمارے پیرامیٹرز کہاں تلاش کیے جائیں۔p？

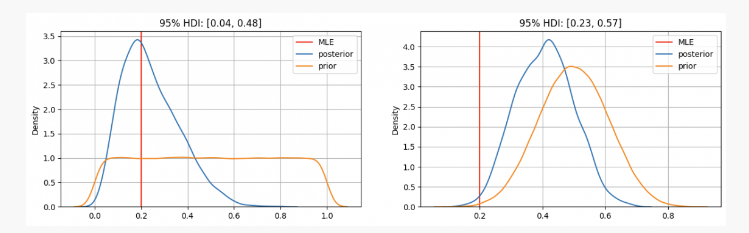
جیسا کہ آپ دیکھ سکتے ہیں، پہلی صورت میں ہمارے پاس ہے۔pکی پیشگی تقسیم زیادہ سے زیادہ امکانی تخمینہ (MLE) پر مرکوز ہےp=0.2، جو فریکوئنٹسٹ طریقہ کا استعمال کرتے ہوئے اسی طرح کا طریقہ ہے۔ حقیقی نامعلوم پیرامیٹر 0.04 اور 0.48 کے درمیان 95% معتبر وقفہ کے اندر موجود ہوگا۔

دوسری طرف، جب اعلی اعتماد ہے کہ پیرامیٹرp جبکہ یہ 0.3 اور 0.7 کے درمیان ہونا چاہیے، ہم دیکھ سکتے ہیں کہ پیچھے کی تقسیم 0.4 کے لگ بھگ ہے، جو ہمارے MLE کی دی گئی قدر سے بہت زیادہ ہے۔ اس صورت میں، حقیقی نامعلوم پیرامیٹر 0.23 اور 0.57 کے درمیان 95% معتبر وقفہ کے اندر موجود ہوگا۔

تو پہلی صورت میں، آپ اپنے دوست کو بتائیں گے کہ آپ کو یقین ہے کہ سکہ غیر منصفانہ ہے۔ لیکن ایک اور معاملے میں، آپ اسے بتائیں گے کہ آپ کو یقین نہیں ہے کہ سکہ درست ہے یا نہیں۔

جیسا کہ آپ دیکھ سکتے ہیں، ایک ہی ثبوت کے ساتھ بھی (10 ٹاس میں سے 2 سر)، مختلف پیشگی عقائد کے پیش نظر نتائج مختلف ہو سکتے ہیں۔ یہ Bayesian اعداد و شمار کی ایک طاقت ہے، جو سائنسی طریقہ کی طرح، ہمیں اپنے عقائد کو نئے مشاہدات اور شواہد کے ساتھ ملا کر اپنے عقائد کو اپ ڈیٹ کرنے کی اجازت دیتی ہے۔

END

آج کے مضمون میں، ہم نے Bayesian اعداد و شمار اور اس کے اہم شراکت داروں کی ابتداء کو دیکھا۔ اس کے بعد سے، شماریات کے اس شعبے میں بہت سے دوسرے اہم شراکت دار ہیں (جیفریز، کاکس، شینن، وغیرہ)، جو quantdare.com سے دوبارہ تیار کیے گئے ہیں۔