Tài nguyên đang được tải lên... tải...

Kiểm tra lại chiến lược cặp đảo ngược trung bình trong ngày giữa SPY và IWM

Tác giả:Tốt, Tạo: 2019-03-28 10:51:06, Cập nhật:

Trong bài viết này, chúng tôi sẽ xem xét chiến lược giao dịch nội ngày đầu tiên của chúng tôi. Nó sẽ sử dụng một ý tưởng giao dịch cổ điển, đó là giao dịch cặp. Trong trường hợp này, chúng tôi sẽ sử dụng hai Quỹ giao dịch trao đổi (ETF), SPY và IWM, được giao dịch trên Sở giao dịch chứng khoán New York (NYSE) và cố gắng đại diện cho các chỉ số thị trường chứng khoán Hoa Kỳ, S&P500 và Russell 2000, tương ứng.

Trong trường hợp này, chúng ta sẽ tính tỷ lệ phòng ngừa rủi ro giữa SPY và IWM thông qua hồi quy tuyến tính lăn. Điều này sau đó sẽ cho phép chúng ta tạo spread giữa SPY và IWM được bình thường hóa thành điểm số z. Các tín hiệu giao dịch sẽ được tạo ra khi điểm số z vượt quá các ngưỡng nhất định dưới niềm tin rằng mức chênh lệch sẽ quay trở lại mức trung bình.

Lý do cho chiến lược là SPY và IWM gần như mô tả cùng một tình huống, đó là kinh tế của một nhóm các tập đoàn Mỹ vốn hóa lớn và vốn hóa nhỏ. tiền đề là nếu người ta lấy mức giá chênh lệch thì nó nên đảo ngược trung bình, vì trong khi các sự kiện địa phương (trong thời gian) có thể ảnh hưởng đến chỉ số S & P500 hoặc chỉ số Russell 2000 riêng biệt (như chênh lệch vốn hóa nhỏ / vốn hóa lớn, ngày tái cân bằng hoặc giao dịch khối), chuỗi giá dài hạn của hai loại có thể sẽ được tích hợp lại.

Chiến lược

Chiến lược được thực hiện theo các bước sau:

Dữ liệu - các thanh 1 phút của SPY và IWM được thu thập từ tháng 4 năm 2007 đến tháng 2 năm 2014.
Xử lý - Dữ liệu được sắp xếp chính xác và các thanh bị thiếu được loại bỏ lẫn nhau.
Spread - Tỷ lệ phòng ngừa rủi ro giữa hai ETF được tính bằng cách sử dụng hồi quy tuyến tính lăn. Điều này được định nghĩa là hệ số hồi quy β bằng cách sử dụng cửa sổ nhìn lại, di chuyển về phía trước 1 bar và tính lại hệ số hồi quy.
Điểm số Z - Điểm số tiêu chuẩn của chênh lệch được tính theo cách thông thường. Điều này có nghĩa là trừ đi trung bình (sample) của chênh lệch và chia cho (sample) độ lệch tiêu chuẩn của chênh lệch. Lý do cho điều này là để làm cho các thông số ngưỡng đơn giản hơn để giải thích vì điểm số z là một số lượng vô chiều. Tôi đã cố tình đưa ra một thiên vị lookahead vào tính toán để cho thấy nó có thể tinh tế như thế nào. Hãy thử và cẩn thận!
Các giao dịch - Các tín hiệu dài được tạo ra khi điểm số z âm giảm xuống dưới ngưỡng đã xác định trước (hoặc sau khi tối ưu hóa), trong khi các tín hiệu ngắn là ngược lại của điều này. Các tín hiệu thoát được tạo ra khi điểm số z tuyệt đối giảm xuống dưới ngưỡng bổ sung. Đối với chiến lược này, tôi đã (một chút tùy tiện) chọn một ngưỡng nhập khẩu tuyệt đối là 10.000z=2 và một ngưỡng thoát là 10.000z=1.

Có lẽ cách tốt nhất để hiểu kỹ hơn về chiến lược là thực hiện nó. Phần sau mô tả một mã Python đầy đủ (tệp duy nhất) để thực hiện chiến lược đảo ngược trung bình này. Tôi đã bình luận rộng rãi về mã để giúp hiểu.

Thực hiện Python

Như với tất cả các hướng dẫn Python / pandas, cần thiết phải thiết lập một môi trường nghiên cứu Python như được mô tả trong hướng dẫn này. Một khi thiết lập, nhiệm vụ đầu tiên là nhập các thư viện Python cần thiết.

Các phiên bản thư viện cụ thể mà tôi đang sử dụng là như sau:

Python - 2.7.3
Số - 1.8.0
panda - 0.12.0
matplotlib - 1.1.0 Chúng ta hãy tiếp tục và nhập các thư viện:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Các hàm sau create_pairs_dataframe nhập hai tập tin CSV chứa các thanh nội ngày của hai ký hiệu. Trong trường hợp của chúng tôi, đây sẽ là SPY và IWM. Sau đó nó tạo một cặp khung dữ liệu riêng biệt, sử dụng các chỉ mục của cả hai tập tin gốc. Vì dấu thời gian của chúng có thể khác nhau do các giao dịch bị bỏ lỡ và lỗi, điều này đảm bảo rằng chúng ta sẽ có dữ liệu phù hợp. Đây là một trong những lợi ích chính của việc sử dụng thư viện phân tích dữ liệu như pandas. Mã boilerplate được xử lý cho chúng ta một cách rất hiệu quả.

# mr_spy_iwm.py

def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""

    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])

    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Bước tiếp theo là thực hiện hồi quy tuyến tính lăn giữa SPY và IWM. Trong trường hợp này IWM là dự đoán (x) và SPY là phản ứng (y). Tôi đã thiết lập cửa sổ xem lại mặc định là 100 thanh. Như đã thảo luận ở trên, đây là một tham số của chiến lược. Để chiến lược được coi là mạnh mẽ, lý tưởng nhất là chúng ta muốn xem hồ sơ trả về (hoặc các thước đo hiệu suất khác) như một hàm cong của khoảng thời gian xem lại. Do đó, ở giai đoạn sau trong mã chúng ta sẽ thực hiện phân tích độ nhạy bằng cách thay đổi khoảng thời gian xem lại trên một phạm vi.

Một khi hệ số beta lăn được tính toán trong mô hình hồi quy tuyến tính cho SPY-IWM, chúng ta thêm nó vào các cặp DataFrame và bỏ các hàng trống. Điều này tạo thành bộ thanh đầu tiên bằng kích thước của lookback như một biện pháp cắt tỉa. Sau đó chúng ta tạo ra sự lây lan của hai ETF như một đơn vị của SPY và −βi đơn vị của IWM. Rõ ràng đây không phải là một tình huống thực tế vì chúng ta đang lấy số lượng phân số của IWM, điều này không thể trong một triển khai thực tế.

Cuối cùng, chúng ta tạo điểm số z của sự lây lan, được tính bằng cách khấu trừ trung bình của sự lây lan và bình thường hóa bằng độ lệch chuẩn của sự lây lan. Lưu ý rằng có một thiên vị lookahead khá tinh tế xảy ra ở đây. Tôi cố tình để lại nó trong mã vì tôi muốn nhấn mạnh việc mắc sai lầm như vậy dễ dàng như thế nào trong nghiên cứu.

# mr_spy_iwm.py

def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
    
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)

    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()

    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Trong create_long_short_market_signals các tín hiệu giao dịch được tạo ra. Chúng được tính bằng cách đi dài chênh lệch khi điểm số z vượt quá điểm số z âm và đi ngắn chênh lệch khi điểm số z vượt quá điểm số z dương.

Để đạt được tình huống này, cần phải biết, cho mỗi thanh, liệu chiến lược là in hoặc out của thị trường. long_market và short_market là hai biến được xác định để theo dõi các vị trí thị trường dài và ngắn. Thật không may, điều này đơn giản hơn nhiều để mã hóa theo cách lặp lại so với cách tiếp cận theo vector và do đó nó chậm tính toán. Mặc dù các thanh 1 phút yêu cầu ~ 700.000 điểm dữ liệu mỗi tệp CSV, nó vẫn tương đối nhanh để tính toán trên máy tính để bàn cũ của tôi!

Để lặp lại trên một Pandas DataFrame (mà thừa nhận không phải là một hoạt động phổ biến) cần phải sử dụng phương pháp iterrows, cung cấp một máy phát điện để lặp lại:

# mr_spy_iwm.py

def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""

    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0

    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0

    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0

    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Ở giai đoạn này, chúng ta đã cập nhật các cặp để chứa các tín hiệu dài / ngắn thực tế, cho phép chúng ta xác định xem chúng ta có cần phải ở trên thị trường hay không. Bây giờ chúng ta cần tạo một danh mục đầu tư để theo dõi giá trị thị trường của các vị trí. Nhiệm vụ đầu tiên là tạo một cột vị trí kết hợp các tín hiệu dài và ngắn. Điều này sẽ chứa một danh sách các yếu tố từ (1,0,−1), với 1 đại diện cho một vị trí dài / thị trường, 0 đại diện cho không có vị trí (nên ra khỏi) và -1 đại diện cho một vị trí ngắn / thị trường. Cột sym1 và sym2 đại diện cho giá trị thị trường của các vị trí SPY và IWM tại cuối mỗi thanh.

Một khi các giá trị thị trường ETF đã được tạo ra, chúng tôi tổng hợp chúng để tạo ra tổng giá trị thị trường ở cuối mỗi thanh. Sau đó nó được chuyển thành một dòng lợi nhuận bằng phương pháp pct_change cho đối tượng Series đó. Các dòng mã tiếp theo xóa các mục không đúng (NaN và các yếu tố inf) và cuối cùng tính đường cong vốn chủ sở hữu đầy đủ.

# mr_spy_iwm.py

def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
    
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()

    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]

    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)

    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

CácchínhCác tập tin CSV trong ngày nằm ở đường datadir. Hãy chắc chắn sửa đổi mã dưới đây để trỏ đến thư mục cụ thể của bạn.

Để xác định mức độ nhạy cảm của chiến lược đối với khoảng thời gian nhìn lại, cần phải tính toán một số liệu hiệu suất cho một phạm vi nhìn lại. Tôi đã chọn tổng tỷ lệ hoàn trả phần trăm cuối cùng của danh mục đầu tư như là thước đo hiệu suất và phạm vi nhìn lại trong [50,200] với các bước gia tăng 10. Bạn có thể thấy trong mã sau rằng các hàm trước được gói trong vòng for trên phạm vi này, với các ngưỡng khác được giữ cố định. Nhiệm vụ cuối cùng là sử dụng matplotlib để tạo biểu đồ đường của nhìn lại so với lợi nhuận:

# mr_spy_iwm.py

if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')

    lookbacks = range(50, 210, 10)
    returns = []

    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)

        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])

    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

Biểu đồ thời gian nhìn lại so với lợi nhuận bây giờ có thể được nhìn thấy. Lưu ý rằng có một tối đa 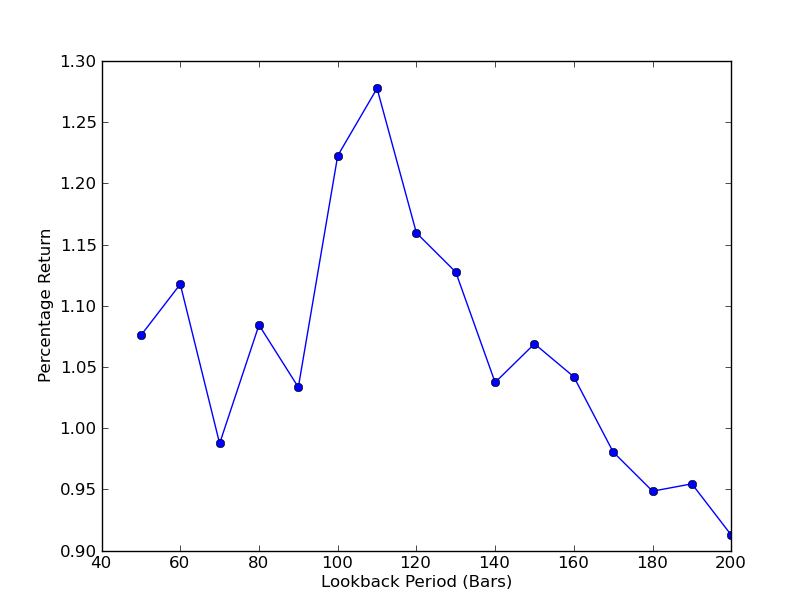global xung quanh một nhìn lại bằng 110 thanh. Nếu chúng ta đã thấy một tình huống mà nhìn lại là độc lập với lợi nhuận điều này sẽ là lý do để lo lắng:Phân tích độ nhạy trong thời gian xem lại tỷ lệ phòng hộ theo hồi quy tuyến tính SPY-IWM

Không có bài báo kiểm tra ngược nào sẽ hoàn thành nếu không có đường cong cổ phần nghiêng lên! Vì vậy, nếu bạn muốn vẽ đường cong của lợi nhuận tích lũy so với thời gian, bạn có thể sử dụng mã sau. Nó sẽ vẽ danh mục đầu tư cuối cùng được tạo từ nghiên cứu tham số xem lại. Do đó, bạn sẽ cần phải chọn xem lại tùy thuộc vào biểu đồ bạn muốn hình dung. Bảng cũng vẽ các lợi nhuận của SPY trong cùng một giai đoạn để hỗ trợ so sánh:

# mr_spy_iwm.py

    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')

    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)

    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)

    fig.show()

Biểu đồ đường cong vốn chủ sở hữu sau đây là cho một thời gian xem lại 100 ngày: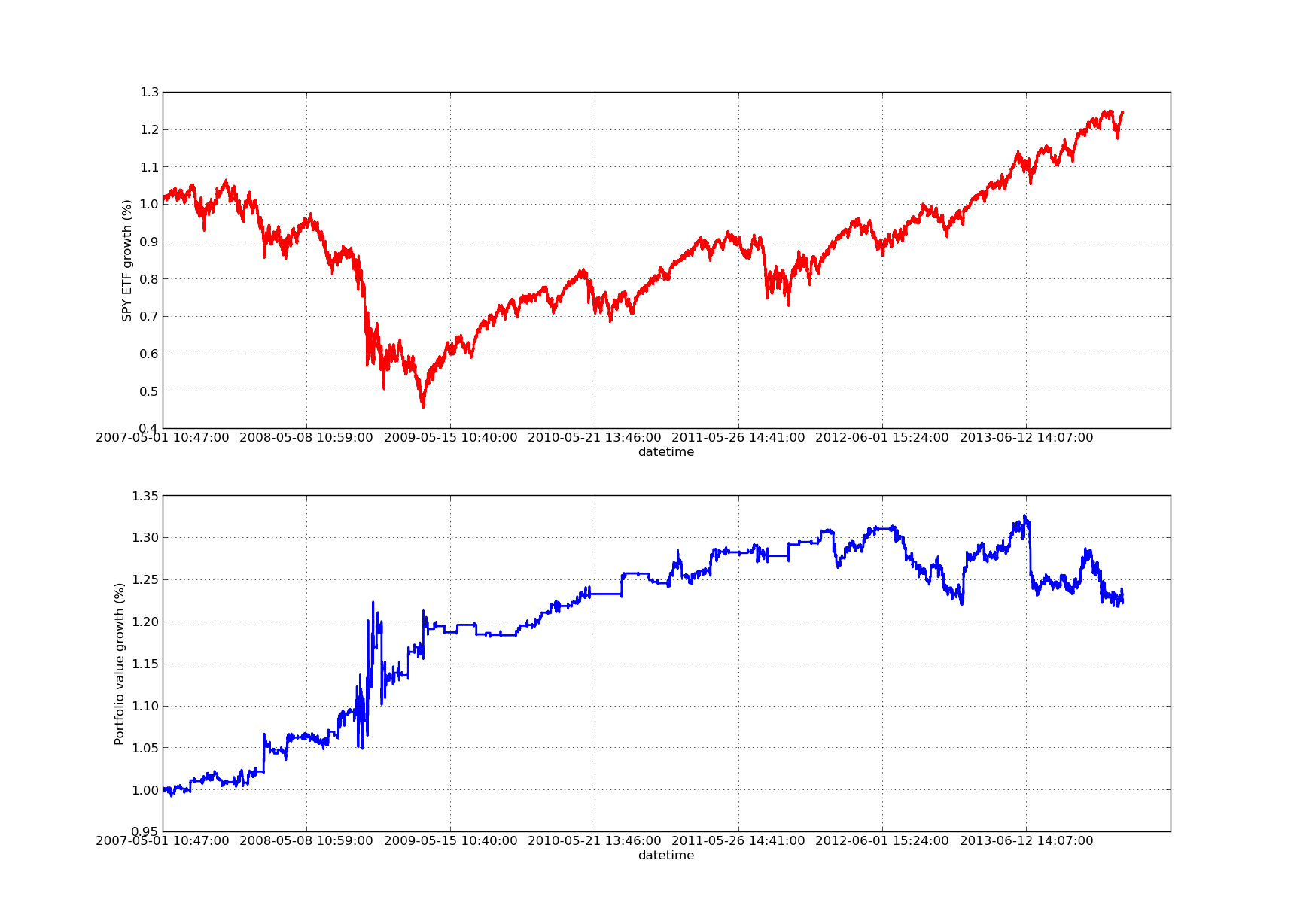Phân tích độ nhạy trong thời gian xem lại tỷ lệ phòng hộ theo hồi quy tuyến tính SPY-IWM

Lưu ý rằng việc rút SPY là đáng kể vào năm 2009 trong giai đoạn khủng hoảng tài chính. Chiến lược cũng có một giai đoạn biến động ở giai đoạn này. Cũng lưu ý rằng hiệu suất đã xấu đi một chút trong năm qua do bản chất xu hướng mạnh mẽ của SPY trong giai đoạn này, phản ánh chỉ số S & P500.

Lưu ý rằng chúng ta vẫn phải tính đến sự thiên vị của người tìm kiếm khi tính toán điểm số z của chênh lệch. Hơn nữa, tất cả các tính toán này đã được thực hiện mà không có chi phí giao dịch. Chiến lược này chắc chắn sẽ hoạt động rất kém một khi các yếu tố này được xem xét. Phí, chênh lệch giá bán / yêu cầu và trượt đều hiện không được tính toán. Ngoài ra, chiến lược đang giao dịch trong các đơn vị phân số của ETF, điều này cũng rất không thực tế.

Trong các bài viết tiếp theo chúng tôi sẽ tạo ra một backtester dựa trên sự kiện phức tạp hơn nhiều sẽ xem xét các yếu tố này và cho chúng tôi nhiều sự tự tin hơn về đường cong vốn chủ sở hữu và số liệu hiệu suất của chúng tôi.

Thêm nữa

2019 FMZ - Tất cả các quyền được bảo lưu