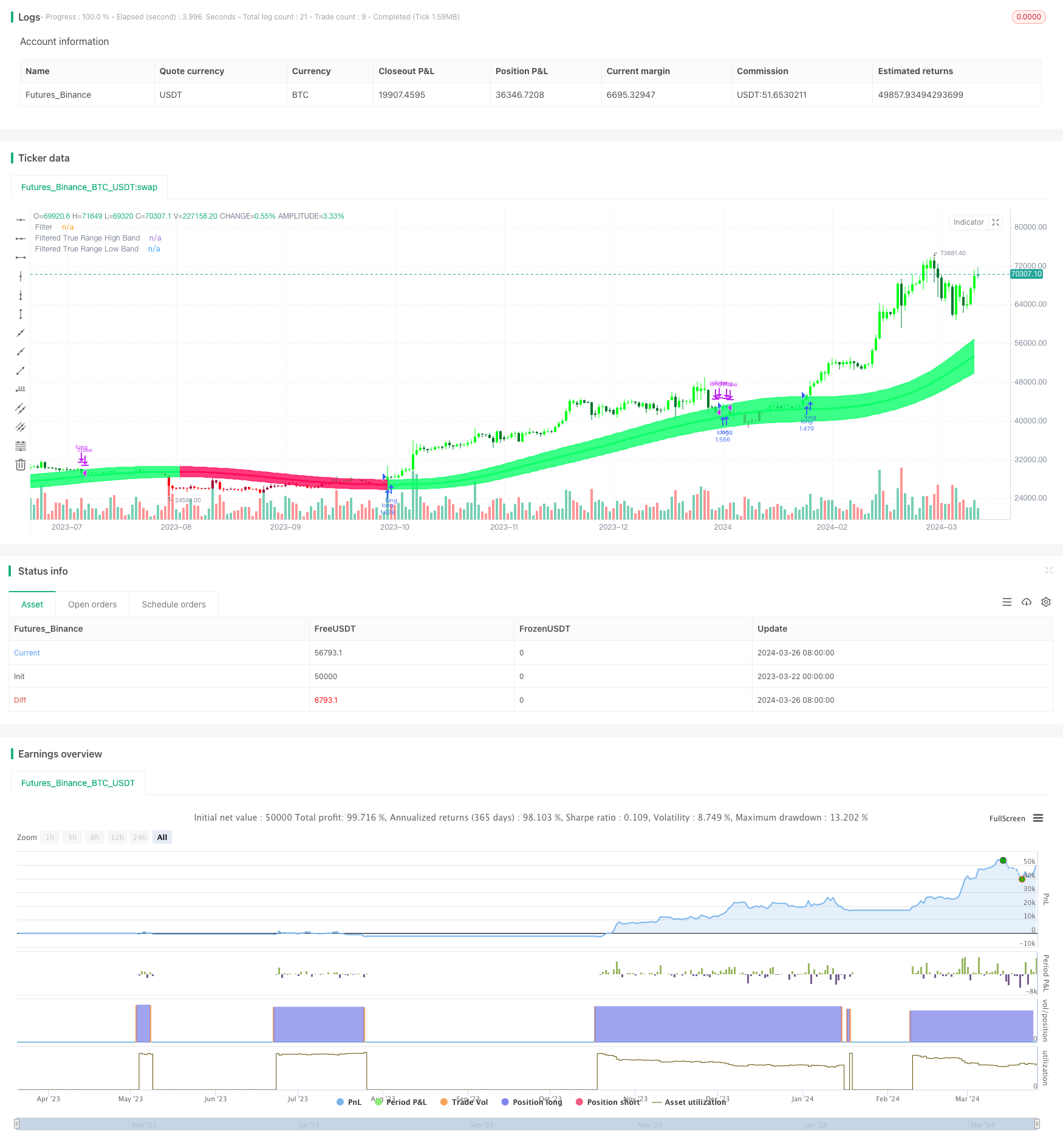
概述

高斯通道自适应均线策略是一种利用高斯滤波技术和自适应参数设置的量化交易策略。该策略基于John Ehlers提出的高斯滤波器理论,通过对价格数据进行多次指数移动平均计算,生成平滑且具有自适应性的交易信号。策略核心是构建一个动态调整的价格通道,上下轨由高斯滤波后的价格加减真实波动幅度得到。当价格突破上轨时进行买入,突破下轨时进行卖出。同时,该策略还引入了时间段参数,可以灵活设置策略运行的起止时间,增强了策略的实用性。

策略原理

高斯通道自适应均线策略的原理如下:

1. 计算价格的高斯滤波值。根据用户设置的采样周期和极点数,计算得到Beta和Alpha参数,然后对价格数据进行逐级高斯滤波,得到平滑处理后的价格序列。
2. 计算真实波动幅度的高斯滤波值。对价格的真实波动幅度进行同样的高斯滤波处理,得到平滑的波动幅度序列。
3. 构建高斯通道。以高斯滤波后的价格为中轨,上轨由中轨加上真实波动幅度与用户设定的倍数的乘积,下轨由中轨减去该值,形成一个动态通道。
4. 生成交易信号。当价格向上突破通道上轨时,产生买入信号;当价格向下突破通道下轨时,产生卖出信号。
5. 引入时间段参数。用户可以设置策略运行的起止时间,在该时间段内策略才会根据交易信号进行操作。

优势分析

高斯通道自适应均线策略具有以下优势:

1. 自适应性强。策略采用动态调整的参数,可以适应不同的市场状态和交易品种,不需要频繁手动调试。
2. 趋势跟踪性好。通过构建价格通道,策略能够较好地捕捉和跟随市场趋势,有效避免震荡市中的虚假信号。
3. 平滑性好。使用高斯滤波技术对价格数据进行多次平滑处理,去除了大部分的市场噪音,使得交易信号更加可靠。
4. 灵活性高。用户可以根据需要调整策略参数,如采样周期、极点数、波动倍数等,以优化策略表现。
5. 实用性强。引入了时间段参数,使得策略可以在指定时间范围内运行,方便实盘应用和回测研究。

风险分析

尽管高斯通道自适应均线策略具有诸多优点,但仍然存在一定的风险:

1. 参数设置风险。不恰当的参数设置可能导致策略失效或表现不佳,因此需要在实际应用中进行反复测试和优化。
2. 突发事件风险。面对某些突发重大事件,策略可能无法及时做出正确反应,造成损失。
3. 过拟合风险。若参数设置过于贴合历史数据,可能导致策略在未来表现欠佳,需要兼顾样本内外的表现。
4. 套利风险。策略主要适用于趋势性市场,在震荡市中若频繁交易,可能面临较大的套利风险。

优化方向

高斯通道自适应均线策略的优化方向包括:

1. 动态参数优化。通过引入机器学习等技术,实现策略参数的自动优化和动态调整,提高适应性。
2. 多因子融合。将其他有效的技术指标或因子与高斯通道相结合,形成更稳健的交易信号。
3. 仓位管理优化。在策略基础上加入合理的仓位管理和资金管理规则,控制回撤和风险。
4. 多品种协同。将策略扩展至多个不同的交易品种,通过资产配置和相关性分析来分散风险。

总结

高斯通道自适应均线策略是一种基于高斯滤波和自适应参数的量化交易策略,通过动态构建价格通道来生成平滑可靠的交易信号。策略具有自适应性强、趋势跟踪性好、平滑性高、灵活性大、实用性强等优点,但同时也面临参数设置、突发事件、过拟合和套利等风险。未来可以从动态参数优化、多因子融合、仓位管理优化、多品种协同等方面对策略进行进一步完善和提升。