ক্যালি সূত্রের পজিশনিং নিয়ন্ত্রণের যন্ত্র

ক্যালি সূত্রের পজিশনিং নিয়ন্ত্রণের যন্ত্র

অনুমান করুন পরাজয় 1: আপনার জয়ের সম্ভাবনা 60% এবং হারানোর সম্ভাবনা 40%; পরাজয়ের ক্ষেত্রে নেট রিটার্নের হার 100% এবং হারানোর ক্ষেত্রে হারানোর হার 100%; অর্থাৎ, যদি আপনি জিতেন তবে আপনি প্রতি 1 ডলারে 1 ডলারের লাভ করতে পারেন এবং যদি আপনি হারেন তবে প্রতি 1 ডলারে 1 ডলারের ক্ষতি হবে। পরাজয়টি সীমাহীনভাবে চলতে পারে এবং প্রতিটি বেতনের নিচে আপনার নিজের পছন্দসইভাবে নির্ধারিত হয়। প্রশ্নঃ অনুমান করুন আপনার প্রাথমিক তহবিল 100 ডলার, তবে আপনি কীভাবে বাজি ধরবেন, অর্থাৎ প্রতিটি বেতনের পরিমাণ মূলধনের কত শতাংশ হতে পারে, দীর্ঘমেয়াদী উপার্জন সর্বাধিক করে তোলে।

• ১। এই পজিশনের জন্য, প্রতিটি বাজিতে প্রত্যাশিত রিটার্নটি বাজির পরিমাণের 60% * 1-40% * 1 = 20%, প্রত্যাশিত রিটার্নটি ইতিবাচক। অর্থাৎ এটি হ্যাকারের পক্ষে একটি পজিশনের সুবিধা এবং খুব বড় সুবিধা রয়েছে।

তাহলে আমরা কিভাবে বাজি ধরব?

যদি আমরা খুব বেশি চিন্তা না করি, খুব কম চিন্তা না করি, তাহলে আমরা মনে করি যেহেতু আমার প্রত্যাশিত রিটার্ন প্রতিটা জয়ের ২০ শতাংশ, তাই দীর্ঘমেয়াদী সর্বোচ্চ রিটার্ন অর্জনের জন্য, আমি প্রতিটা জয়ে যতটা সম্ভব মূলধন বিনিয়োগ করতে চাই। এই হার সর্বোচ্চ ১০০ শতাংশ।

তবে স্পষ্টতই প্রতিটি রাউন্ড জুয়া খেলতে 100% মূলধন রাখা অযৌক্তিক, কারণ একবার জুয়া খেলোয়াড় হেরে গেলে সমস্ত মূলধন হারাতে হবে এবং পরবর্তী রাউন্ডে অংশ নিতে পারবেন না। দীর্ঘমেয়াদে, জুয়া খেলোয়াড়রা একবার হেরে গেলে এই ঘটনাটি অবশ্যই ঘটবে, তাই দীর্ঘমেয়াদে অবশ্যই দেউলিয়া হবে।

সুতরাং, এখানে একটি উপসংহার পাওয়া যায়ঃ যখনই একটি পজিটিভ স্ট্যাটাস বিদ্যমান থাকে, তখনই সমস্ত মূলধন একসাথে হারাতে পারে, যদিও এটি খুব ছোট হতে পারে, তবে এটি কখনই পূর্ণ হতে পারে না। কারণ দীর্ঘমেয়াদে, ছোট সম্ভাব্যতা ইভেন্টগুলি অবশ্যই ঘটবে, এবং বাস্তব জীবনে, একটি ছোট সম্ভাব্যতা ইভেন্টের প্রকৃত সম্ভাব্যতা তার তাত্ত্বিক সম্ভাব্যতার চেয়ে অনেক বেশি। এটি অর্থনীতিতে চর্বিযুক্ত শেষের প্রভাব।

• ২, স্থবিরতা ১-এ ফিরে যান। যেহেতু প্রতিবার ১০০% বাজি রাখাটা যুক্তিযুক্ত নয়, তাহলে ৯৯% বাজি রাখাটা কি যুক্তিযুক্ত?

কিন্তু বাস্তবে কি এমনটা হচ্ছে?

আমরা এই সমস্যাটি তত্ত্বগতভাবে বিশ্লেষণ করার পরিবর্তে একটি পরীক্ষা করতে পারি। আমরা এই পজিশনটি সিমুলেট করি এবং প্রতিবার ৯৯% বাজি ধরে দেখি ফলাফল কী হয়।

এই মডেলটি খুব সহজ এবং এটি এক্সেল দিয়ে করা যেতে পারে।

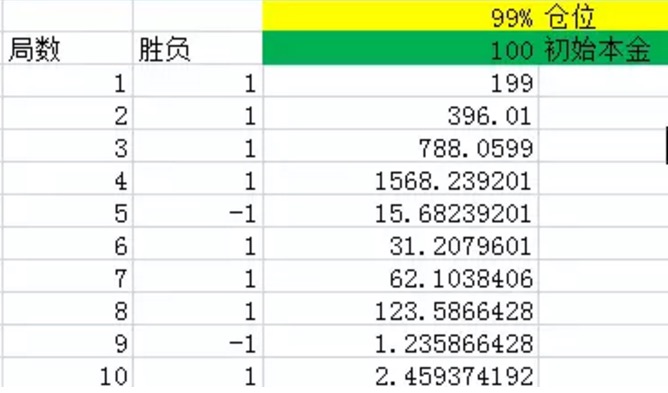চিত্র ১

উপরের চিত্রের মতো, প্রথম কলামটি পয়েন্ট সংখ্যাকে নির্দেশ করে। দ্বিতীয় কলামটি হেরেছে, এক্সেল 60% সম্ভাবনা অনুসারে 1 উত্পাদন করবে, অর্থাৎ 60% সম্ভাবনা, নেট রিটার্নের সম্ভাবনা 1,40% সম্ভাবনা, -1 উত্পাদন করবে, অর্থাৎ 40% সম্ভাবনা, নেট রিটার্নের সম্ভাবনা -1। তৃতীয় কলামটি হ'ল প্রতিটি রাউন্ডের শেষে হ্যাকারের সমস্ত তহবিল। এই পরীক্ষার প্রতিটি বেতনের পরিমাণ 99% এবং প্রাথমিক মূলধন 100। যথাক্রমে হলুদ এবং সবুজ চিহ্নিত করা হয়েছে।

আপনি গ্রাফ থেকে দেখতে পাচ্ছেন যে, ১০ টি রাউন্ডের পরে, ১০ টি রাউন্ডের মধ্যে ৮ টিতে জয়ী হওয়ার সম্ভাবনা ৬০% এর চেয়েও বেশি, মাত্র দুবার হেরেছে। কিন্তু এমনকি এটির পরেও, শেষ অর্থটি কেবল ২.৪৬ ইউয়ান বাকি রয়েছে, যা মূলত হারাতে হবে।

যখন আমি পরীক্ষার সংখ্যা বাড়িয়ে ১০০০, ২০০০, ৩০০০... করেছি, তখন এটা স্পষ্ট যে, শেষ পর্যন্ত হাতে থাকা অর্থের পরিমাণ মূলত ০-এর দিকে যাচ্ছে।

এবং যেহেতু ৯৯% কাজ করে না, তাহলে আসুন আমরা কিছু অন্যান্য অনুপাতের সাথে চেষ্টা করি, এবং নিচের চিত্রটি দেখুনঃ চিত্র থেকে দেখা যায় যে, যখন পজিশন ধীরে ধীরে কমিয়ে ৯৯% থেকে ৯০%, ৮০%, ৭০, ৬০% করা হয়, তখন একই ১০ টি রাউন্ডের ফলাফল একেবারে ভিন্ন হয়।

এখানে দেখলে বুঝতে পারবেন যে, এই পজিশনের সমস্যাটা এত সহজ নয়। এমনকি হ্যাকাররা এত বড় পজিশনেও, এখান থেকে টাকা পাওয়া সহজ নয়।

তাহলে দীর্ঘমেয়াদে সর্বোচ্চ লাভের জন্য কীভাবে বাজি ধরবেন?

উপরের চিত্রের মতো, অনুপাত যত ছোট হবে তত ভাল হবে? না, কারণ যখন অনুপাত শূন্য হয়ে যায় তখন স্পষ্টতই অর্থ উপার্জন করা যায় না।

তাহলে এই অনুপাত কত?

এটিই সেই সমস্যা, যেটা কেলির বিখ্যাত সূত্রের মাধ্যমে সমাধান করা হয়েছে!

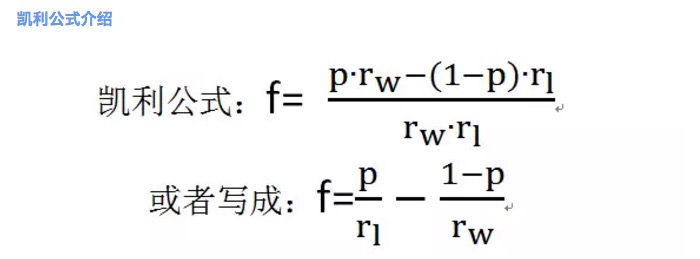চিত্র ২

যেখানে f হল সর্বোত্তম বাজির অনুপাত; p হল জেতার সম্ভাবনা; rw হল জেতার সময় নেট রিটার্ন হার, যেমনঃ rw=1 in deadlock 1; rl হ'ল হারানোর সময় নেট লস হার, যেমনঃ rl=1 in deadlock 1; লক্ষ্য করুন এখানে rl>0।

ক্যালি সূত্র অনুযায়ী, প্যাডম্যাচ ১-এ সর্বোচ্চ বাজি ২০%।

আমরা একটি পরীক্ষা চালিয়ে এই উপসংহারটি আরও গভীরভাবে বুঝতে পারি।

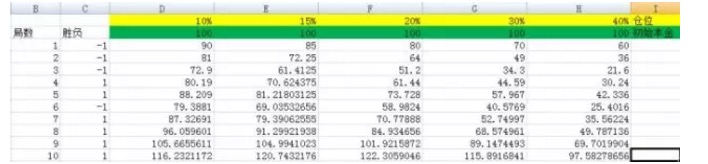চিত্র ৩

উদাহরণস্বরূপ, আমরা পজিশনগুলোকে ১০, ১৫, ২০, ৩০, ৪০% এ সেট করেছি। তাদের কলামের সংখ্যা হচ্ছে D, E, F, G, H।

এবং যখন আমি আমার পরীক্ষার সংখ্যা ৩০০০ বার করে দিলাম, এবং যখন আমি আমার পরীক্ষার সংখ্যা ৫০০০-এ রূপান্তরিত করি, আপনি দেখতে পাচ্ছেন যে F কলামের ফলাফল সবচেয়ে বড়, এবং অন্যান্য কলামের তুলনায় ফ্রেজিং একটি সংখ্যাগত স্কেল নয়। এবং F কলামের অবস্থান অনুপাত 20%।

আপনি কি ক্যালি সূত্রের শক্তি দেখতে পাচ্ছেন? উপরের পরীক্ষায়, যদি আপনি দুর্ভাগ্যবশত 40% বাছাই করেন, যা H কলামের সাথে সম্পর্কিত হয়, তাহলে 5000 রানের পরে আপনার মূলধন 100 থেকে 22799985.75 হয়ে যায়, তবে এটি একটি বিশাল লাভ। কিন্তু 20% এর ফলাফলের তুলনায় এটি অর্থ উপার্জনের সমান।

এটিই জ্ঞানের শক্তি!

• ৩, কেলি সূত্রের ব্যাখ্যা

কেলি সূত্রের গাণিতিক সূচক এবং এর জটিলতা, যা খুব গভীর গাণিতিক জ্ঞান প্রয়োজন, তাই এখানে আলোচনা করার কোন মানে নেই। এখানে আমি কিছু পরীক্ষার মাধ্যমে কেলি সূত্রের বিষয়গত বোঝার গভীরতা বাড়াবো।

আসুন আমরা আরেকটি প্যাকেজ দেখি। প্যাকেজ ২ঃ আপনার হারার এবং জেতার সম্ভাবনা ৫০%। যেমনঃ মুদ্রা ছুঁড়ে ফেলা। জেতার সময় নেট রিটার্ন ১, অর্থাৎ rw=১, হারার সময় নেট লস ০.৫, অর্থাৎ rl=০.৫। অর্থাৎ, আপনি যখনই ১ ইউএস ডলার জিতবেন, তখনই আপনি ১ ইউএস ডলার জিতবেন, যখনই আপনি হারাবেন তখনই আপনি ৫ ইউএস ডলার দেবেন।

এটা সহজেই দেখা যায় যে, হ্যাকিংয়ের দ্বিতীয় পর্বের প্রত্যাশিত মুনাফা ছিল ০.২৫। এই পর্বটি হ্যাকারদের জন্য অত্যন্ত সুবিধাজনক।

ক্যালি সূত্র অনুসারে, আমরা প্রতি রাউন্ডে সর্বোত্তম বাজির অনুপাত পেতে পারিঃ

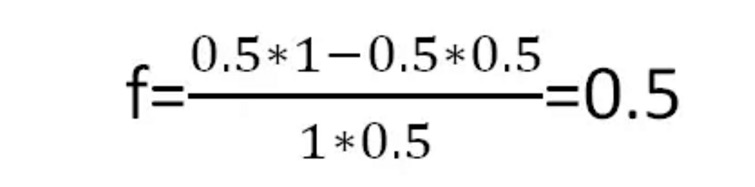চিত্র ৪

অর্থাৎ, প্রতিবার অর্ধেক টাকা নিয়ে বাজি ধরলে দীর্ঘমেয়াদে সর্বোচ্চ লাভ পাওয়া যায়।

নিচে আমি গড় বৃদ্ধির হার r এর ধারণার উপর ভিত্তি করে একটি পরীক্ষা করব।

প্রথমত, পরীক্ষা ২.১ দেখুন, এখানে দুটি চিত্র রয়েছেঃ

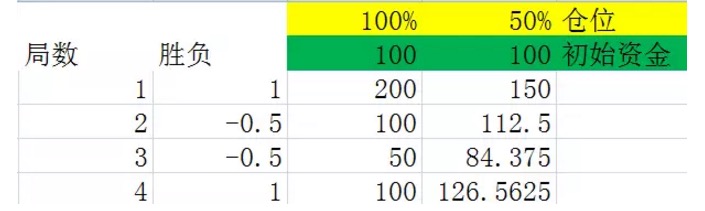চিত্র ৫

এই দুটি চিত্রই হল অ্যালগরিদমিক প্যাকেজ ২-এর একটি পরীক্ষা। দ্বিতীয় কলামের বিজয়ী কলামে পরীক্ষার ৫০% সম্ভাবনা রয়েছে ১, যার অর্থ হল ১০০% লাভ। ৫০% সম্ভাবনা রয়েছে -০.৫, যার অর্থ হল ৫০% ক্ষতি। তৃতীয় এবং চতুর্থ কলামে পজিশনের ১০০% এবং ৫০% এর নিচে প্রতিটি প্যাকেজ পেরিয়ে থাকা অর্থ রয়েছে।

দুইটি চার্টকে সাবধানে তুলনা করলে একটি উপসংহার পাওয়া যায়, অর্থাৎ একই সংখ্যক চার্ট অতিক্রম করার পর, চূড়ান্ত ফলাফল শুধুমাত্র এই চার্টগুলির মধ্যে জয়ী এবং হারানো সংখ্যার সাথে সম্পর্কিত, এবং এই চার্টগুলির মধ্যে জয়ী এবং হারানো সংখ্যার সাথে সম্পর্কিত নয়। উদাহরণস্বরূপ, উপরের দুটি চার্টগুলিতে, একইভাবে চারটি চার্ট করা হয়েছে, একইভাবে প্রতিটি চার্টগুলিতে দুটি চার্ট জিতেছে দুটি চার্ট হারিয়েছে, তবে প্রথম চার্টের হারানো আদেশটি জয়ী হারিয়েছে, দ্বিতীয় চার্টের হারানো আদেশটি হারিয়েছে। শেষ পর্যন্ত তাদের ফলাফল একই।

অবশ্যই, এই সিদ্ধান্তটি খুব সহজেই প্রমাণিত হয় (যদিও গুণের বিনিময় সূত্রটি প্রাথমিক বিদ্যালয়ের শিক্ষার্থীদের কাছে প্রমাণিত হয়), তবে এখানে প্রমাণিত হয় না যে উপরের দুটি উদাহরণ আমাদের জন্য যথেষ্ট ভাল বোঝার জন্য যথেষ্ট।

সুতরাং, যেহেতু শেষ ফলাফলটি জয়-হেরে যাওয়ার ক্রমের সাথে সম্পর্কিত নয়, তাই আমরা অনুমান করি যে পজিটিভ 2 পরীক্ষা 2.2 এর মতো চলতে থাকে, এবং নীচের চিত্রটি দেখুনঃ

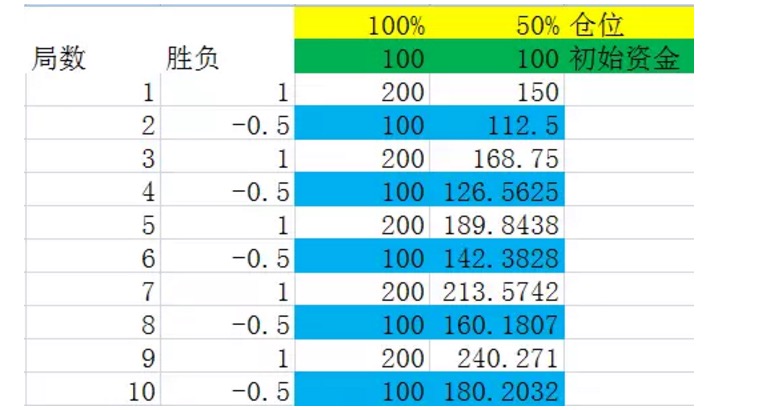চিত্র ৬

আমরা অনুমান করি যে প্যাকেজগুলির বিজয়গুলি পরিবর্তিত হয়, যেহেতু প্রথম উপসংহারটি দীর্ঘমেয়াদে ফলাফলের অর্থের উপর কোনও প্রভাব ফেলে না।

ছবিটি দেখার আগে, আমরা একটি সংজ্ঞা তৈরি করি। ধরুন, আমরা একটি সমষ্টিকে একটি সমষ্টি হিসাবে বিবেচনা করি, যার মধ্যে বিভিন্ন ফলাফলের ফ্রিকোয়েন্সি তার সম্ভাব্যতার সমান, এবং এই সমষ্টিটি সমস্ত শর্ত পূরণের সমষ্টির মধ্যে সর্বনিম্ন সংখ্যক সমষ্টি। আমরা এই সমষ্টিকে একটি সমষ্টি বলি। উদাহরণস্বরূপ, উপরের চিত্রের পরীক্ষায়, একটি সমষ্টিটি দুটি সমষ্টিকে উপস্থাপন করে, যার মধ্যে একটি জয় এবং একটি হার।

উপরের চিত্রের নীল চিহ্নিত সংখ্যাগুলিকে ঘনিষ্ঠভাবে দেখুন, এগুলি একটি পজিশনের শেষ। আপনি দেখতে পাবেন যে এই সংখ্যাগুলি স্থিতিশীল বৃদ্ধি বজায় রেখেছে। যখন পজিশন 100% হয়, তখন নীল চিহ্নিত সংখ্যার বৃদ্ধি হার 0% হয়, অর্থাৎ পজিশনের পরে মূলধনের বৃদ্ধি হার 0% হয়। এটিও ব্যাখ্যা করে যে যখন প্রতিটি পজিশন পূর্ণ হয়, তখন পজিশন 2 এর মাঝামাঝি দীর্ঘমেয়াদে অর্থ উপার্জন করা অসম্ভব। যখন পজিশন 50% হয় (যেমন কেলির সূত্রের সেরা অনুপাত) তখন নীল চিহ্নিত সংখ্যার বৃদ্ধি হার 12.5%, অর্থাৎ পজিশনের পরে মূলধনের বৃদ্ধি হার 12.5% হয়।

এটি একটি সর্বজনীন নিয়ম যে, প্রতিটি প্যাকেজ বন্ধ হওয়ার পরে বৃদ্ধির হার পজিশনের সাথে সম্পর্কিত। এবং প্রতিটি প্যাকেজ বন্ধ হওয়ার পরে বৃদ্ধির হার যত বেশি, দীর্ঘমেয়াদে চূড়ান্ত লাভ তত বেশি।

প্রতিটি প্যাকেজের বৃদ্ধি হারের উপর ভিত্তি করে প্রতি প্যাকেজের গড় বৃদ্ধি হারের গণনা করা যায় g. উপরের চিত্রটিতে, যদি প্যাকেজের প্রতিটি প্যাকেজে দুটি প্যাকেজ থাকে, তবে প্রতিটি প্যাকেজের গড় বৃদ্ধি হারের গণনা করা হয়।

চিত্র ৭

দীর্ঘমেয়াদে, মূলধন সর্বাধিক বৃদ্ধি পেতে চান, আসলে যতক্ষণ r সর্বাধিক করা হয়, অর্থাৎ g সর্বাধিক করা হয়; এবং সর্বোত্তম বাজি অনুপাত f আসলে max ((g) সমাধানের মাধ্যমে পাওয়া যায়।

• ৪. ক্যালি সূত্রের অন্যান্য উপসংহার > কেলি কিংবদন্তি

ক্যালি সূত্রটি মূলত এটি&টি বেল ল্যাবরেটরির পদার্থবিজ্ঞানী জন ল্যারি ক্যালি দ্বারা তৈরি করা হয়েছিল, যা তার সহকর্মী ক্লাউড এলউড শ্যাননের দীর্ঘ পথের টেলিফোন লাইন ম্যাগাজিনের গবেষণার ভিত্তিতে তৈরি করা হয়েছিল। ক্যালি শ্যাননের তথ্য তত্ত্বকে কীভাবে একটি অভ্যন্তরীণ বার্তা থাকা একজন জুয়াড়িকে ঘোড়ায় চড়ার সময় প্রয়োগ করতে হবে তা সমাধান করেছিলেন। জুয়াড়িটি সেরা বাজি নির্ধারণ করতে চান, এবং তার অভ্যন্তরীণ বার্তাটি নিখুঁত হতে হবে না, তবে এটি তাকে একটি দরকারী সুবিধা দেবে। ক্যালি সূত্রটি তারপরে শ্যাননের অন্য সহকর্মী এডওয়ার্ড সোপ দ্বারা ব্যবহার করা হয়েছিল একুশ পয়েন্ট এবং স্টক মার্কেটে। সোপ তার কাজ থেকে কয়েক মাসের কঠোর পরিশ্রমের মাধ্যমে একটি গণিতের প্রবন্ধ লিখেছিলেন যার শিরোনাম ছিল "২১ পয়েন্ট জয়ের সর্বোত্তম কৌশল"। তিনি তার জ্ঞান ব্যবহার করেছিলেন এবং রাতারাতি নেভাদার রেনোর সমস্ত ক্যাসিনোতে হামলা চালিয়েছিলেন এবং একুশ পয়েন্ট জয়ের টেবিলে সফলভাবে কয়েক হাজার ডলার জিতেছিলেন। তিনি মার্কিন যুক্তরাষ্ট্রের ওয়াল স্ট্রিট কোয়ালিফাইড ট্রেডিং হেজিং ফান্ডের জনক এবং 1970 এর দশকে প্রথম কোয়ালিফাইড ট্রেডিং হেজিং ফান্ড তৈরি করেছিলেন। ১৯৬২ সালে তিনি তার বিশেষায়িত বই প্রকাশ করেছিলেন যা জমিদারদের পরাজিত করে এবং এটি অর্থনীতির একটি ক্লাসিক বই হয়ে ওঠে।

ব্যবহারিক দৃষ্টিভঙ্গি

কিভাবে কেলি সূত্র ব্যবহার করে বাস্তব জীবনে অর্থ উপার্জন করা যায়? আমি মনে করি, এই প্যাকেজটি অবশ্যই আর্থিক বাজার থেকে আসবে। আমি সম্প্রতি ট্রেডিং সিস্টেম নিয়ে গবেষণা করছি এবং একটি ভাল ট্রেডিং সিস্টেমের জন্য সবচেয়ে গুরুত্বপূর্ণ কি? একটি প্রত্যাশিত রিটার্ন ইতিবাচক কেনার এবং বিক্রয়ের নিয়মের জন্য 10% গুরুত্বপূর্ণ, একটি ভাল তহবিল নিয়ন্ত্রণ পদ্ধতির জন্য 40% গুরুত্বপূর্ণ, এবং বাকি 50% মানুষের মানসিক নিয়ন্ত্রণের জন্য। ক্যালি ফর্মুলা হচ্ছে সেই হাতিয়ার যা আমাকে তহবিলের অবস্থান নিয়ন্ত্রণ করতে সাহায্য করে। উদাহরণস্বরূপ, আমি আগে একটি স্টক ট্রেডিং সিস্টেম নিয়ে গবেষণা করেছি, যেখানে প্রতি সপ্তাহে ০.৮ শতাংশ ট্রেডিং সফল হয় এবং ০.২ শতাংশ ট্রেডিং ব্যর্থ হয়। সফল হলে ৩ শতাংশ লাভ হয় (কমিশন, স্ট্যাম্পিং ট্যাক্স ছাড়িয়ে) এবং ব্যর্থ হলে ৫ শতাংশ ক্ষতি হয়। কেলি ফর্মুলা না জানার আগে আমি অন্ধভাবে পূর্ণ ট্রেডিং করতাম এবং আমি জানতাম না যে এই অবস্থানটি ঠিক কিনা। এটি মানসিকভাবে ভ্রান্ত। কেলি ফর্মুলা ব্যবহার করার পরে, গণনা করার জন্য সর্বোত্তম অবস্থানটি হতে হবে ৯.৩৩, অর্থাৎ যদি আপনি ঋণের সুদের হার ০ চান তবে দ্রুততম মূলধন বৃদ্ধির হার পেতে পারেন। অবশ্যই, কেলি সূত্রের ব্যবহারিক প্রয়োগে এটি এত সহজ হতে পারে না, এবং অনেকগুলি অসুবিধা রয়েছে যা মোকাবেলা করা দরকার। উদাহরণস্বরূপ, লিভারেজ এক্সচেঞ্জের জন্য প্রয়োজনীয় মূলধন ব্যয়, যেমন বাস্তব অর্থের অর্থের সীমাহীন বিভাজকতা নেই, যেমন আর্থিক বাজারে উপরে উল্লিখিত সহজ প্যাকেজ হিসাবে সহজ নয়। তবে যাই হোক, ক্যালি সূত্র আমাদের সামনে এগিয়ে যাওয়ার পথ দেখায়।