1. বর্গক্ষেত্র
2. ডেল্টা-আরএসআই দোলক কৌশল

ডেল্টা-আরএসআই দোলক কৌশল

লেখক:চাওঝাং, তারিখঃ ২০২২-০৫-৩০ ১১ঃ১১ঃ০২
ট্যাগঃআরএসআই

---

---

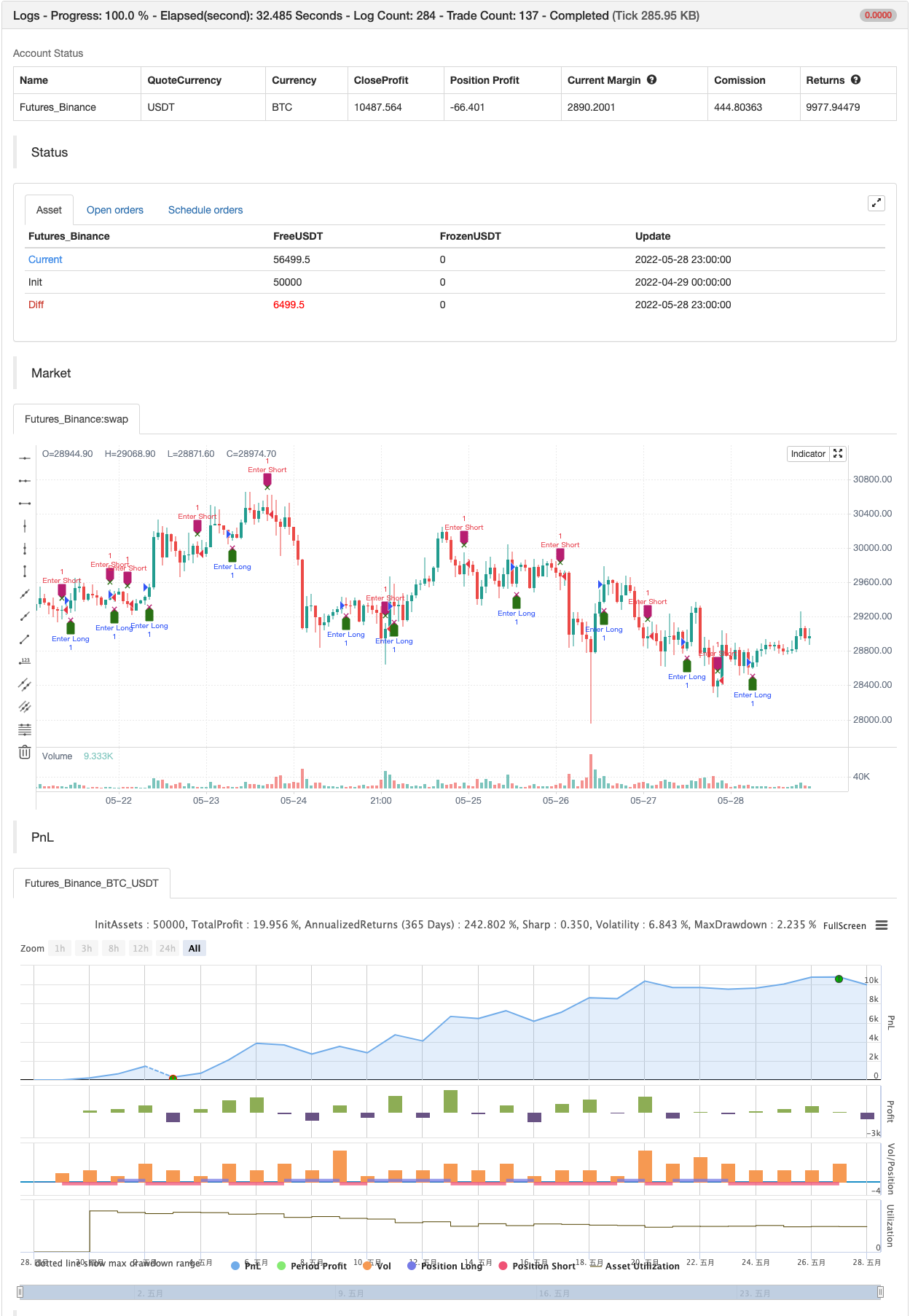
/*backtest
start: 2022-04-29 00:00:00
end: 2022-05-28 23:59:00
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/

// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © tbiktag
//
// Delta-RSI Oscillator Strategy
//
// A strategy that uses Delta-RSI Oscillator (© tbiktag) as a stand-alone indicator:
// https://www.tradingview.com/script/OXQVFTQD-Delta-RSI-Oscillator/
//
// Delta-RSI is a smoothed time derivative of the RSI, plotted as a histogram 
// and serving as a momentum indicator. 
// 
// Input parameters:
// RSI Length: The timeframe of the RSI that serves as an input to D-RSI.
// Length: The length of the lookback frame used for local regression.
// Polynomial Order: The order of the local polynomial function used to interpolate the RSI.
// Signal Length: The length of a EMA of the D-RSI series that is used as a signal line.
// Trade signals are generated based on three optional conditions:
// - Zero-crossing: bullish when D-RSI crosses zero from negative to positive values (bearish otherwise)
// - Signal Line Crossing: bullish when D-RSI crosses from below to above the signal line (bearish otherwise)
// - Direction Change: bullish when D-RSI was negative and starts ascending (bearish otherwise)
//
// Since D-RSI oscillator is based on polynomial fitting of the RSI curve, there is also an option
// to filter trade signal by means of the root mean-square error of the fit (normalized by the sample average).
// 
//@version=4
study(title="Delta-RSI Oscillator Strategy", shorttitle = "D-RSI", overlay = true)

// ---Subroutines---
matrix_get(_A,_i,_j,_nrows) =>
    // Get the value of the element of an implied 2d matrix
    //input: 
    // _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _i :: integer: row number
    // _j :: integer: column number
    // _nrows :: integer: number of rows in the implied 2d matrix
    array.get(_A,_i+_nrows*_j)

matrix_set(_A,_value,_i,_j,_nrows) =>
    // Set a value to the element of an implied 2d matrix
    //input: 
    // _A :: array, changed on output: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _value :: float: the new value to be set
    // _i :: integer: row number
    // _j :: integer: column number
    // _nrows :: integer: number of rows in the implied 2d matrix
    array.set(_A,_i+_nrows*_j,_value)

transpose(_A,_nrows,_ncolumns) =>
    // Transpose an implied 2d matrix
    // input:
    // _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _nrows :: integer: number of rows in _A
    // _ncolumns :: integer: number of columns in _A
    // output:
    // _AT :: array: pseudo 2d matrix with implied dimensions: _ncolums x _nrows
    var _AT = array.new_float(_nrows*_ncolumns,0)
    for i = 0 to _nrows-1
        for j = 0 to _ncolumns-1
            matrix_set(_AT, matrix_get(_A,i,j,_nrows),j,i,_ncolumns)
    _AT

multiply(_A,_B,_nrowsA,_ncolumnsA,_ncolumnsB) => 
    // Calculate scalar product of two matrices
    // input: 
    // _A :: array: pseudo 2d matrix
    // _B :: array: pseudo 2d matrix
    // _nrowsA :: integer: number of rows in _A
    // _ncolumnsA :: integer: number of columns in _A
    // _ncolumnsB :: integer: number of columns in _B
    // output:
    // _C:: array: pseudo 2d matrix with implied dimensions _nrowsA x _ncolumnsB
    var _C = array.new_float(_nrowsA*_ncolumnsB,0)
    int _nrowsB = _ncolumnsA
    float elementC= 0.0
    for i = 0 to _nrowsA-1
        for j = 0 to _ncolumnsB-1
            elementC := 0
            for k = 0 to _ncolumnsA-1
                elementC := elementC + matrix_get(_A,i,k,_nrowsA)*matrix_get(_B,k,j,_nrowsB)
            matrix_set(_C,elementC,i,j,_nrowsA)
    _C

vnorm(_X,_n) =>
    //Square norm of vector _X with size _n
    float _norm = 0.0
    for i = 0 to _n-1
        _norm := _norm + pow(array.get(_X,i),2)
    sqrt(_norm)

qr_diag(_A,_nrows,_ncolumns) => 
    //QR Decomposition with Modified Gram-Schmidt Algorithm (Column-Oriented)
    // input:
    // _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
    // _nrows :: integer: number of rows in _A
    // _ncolumns :: integer: number of columns in _A
    // output:
    // _Q: unitary matrix, implied dimenstions _nrows x _ncolumns
    // _R: upper triangular matrix, implied dimansions _ncolumns x _ncolumns
    var _Q = array.new_float(_nrows*_ncolumns,0)
    var _R = array.new_float(_ncolumns*_ncolumns,0)
    var _a = array.new_float(_nrows,0)
    var _q = array.new_float(_nrows,0)
    float _r = 0.0
    float _aux = 0.0
    //get first column of _A and its norm:
    for i = 0 to _nrows-1
        array.set(_a,i,matrix_get(_A,i,0,_nrows))
    _r := vnorm(_a,_nrows)
    //assign first diagonal element of R and first column of Q
    matrix_set(_R,_r,0,0,_ncolumns)
    for i = 0 to _nrows-1
        matrix_set(_Q,array.get(_a,i)/_r,i,0,_nrows)
    if _ncolumns != 1
        //repeat for the rest of the columns
        for k = 1 to _ncolumns-1
            for i = 0 to _nrows-1
                array.set(_a,i,matrix_get(_A,i,k,_nrows))
            for j = 0 to k-1
                //get R_jk as scalar product of Q_j column and A_k column:
                _r := 0
                for i = 0 to _nrows-1
                    _r := _r + matrix_get(_Q,i,j,_nrows)*array.get(_a,i)
                matrix_set(_R,_r,j,k,_ncolumns)
                //update vector _a
                for i = 0 to _nrows-1
                    _aux := array.get(_a,i) - _r*matrix_get(_Q,i,j,_nrows)
                    array.set(_a,i,_aux)
            //get diagonal R_kk and Q_k column
            _r := vnorm(_a,_nrows)
            matrix_set(_R,_r,k,k,_ncolumns)
            for i = 0 to _nrows-1
                matrix_set(_Q,array.get(_a,i)/_r,i,k,_nrows)
    [_Q,_R]
    
pinv(_A,_nrows,_ncolumns) =>
    //Pseudoinverse of matrix _A calculated using QR decomposition
    // Input: 
    // _A:: array: implied as a (_nrows x _ncolumns) matrix _A = [[column_0],[column_1],...,[column_(_ncolumns-1)]]
    // Output: 
    // _Ainv:: array implied as a (_ncolumns x _nrows) matrix _A = [[row_0],[row_1],...,[row_(_nrows-1)]]
    // ----
    // First find the QR factorization of A: A = QR,
    // where R is upper triangular matrix.
    // Then _Ainv = R^-1*Q^T.
    // ----
    [_Q,_R] = qr_diag(_A,_nrows,_ncolumns)
    _QT = transpose(_Q,_nrows,_ncolumns)
    // Calculate Rinv:
    var _Rinv = array.new_float(_ncolumns*_ncolumns,0)
    float _r = 0.0
    matrix_set(_Rinv,1/matrix_get(_R,0,0,_ncolumns),0,0,_ncolumns)
    if _ncolumns != 1
        for j = 1 to _ncolumns-1
            for i = 0 to j-1
                _r := 0.0
                for k = i to j-1
                    _r := _r + matrix_get(_Rinv,i,k,_ncolumns)*matrix_get(_R,k,j,_ncolumns)
                matrix_set(_Rinv,_r,i,j,_ncolumns)
            for k = 0 to j-1
                matrix_set(_Rinv,-matrix_get(_Rinv,k,j,_ncolumns)/matrix_get(_R,j,j,_ncolumns),k,j,_ncolumns)
            matrix_set(_Rinv,1/matrix_get(_R,j,j,_ncolumns),j,j,_ncolumns)
    //
    _Ainv = multiply(_Rinv,_QT,_ncolumns,_ncolumns,_nrows)
    _Ainv

norm_rmse(_x, _xhat) =>
    // Root Mean Square Error normalized to the sample mean
    // _x.   :: array float, original data
    // _xhat :: array float, model estimate
    // output
    // _nrmse:: float
    float _nrmse = 0.0
    if array.size(_x) != array.size(_xhat)
        _nrmse := na
    else
        int _N = array.size(_x)
        float _mse = 0.0
        for i = 0 to _N-1
            _mse := _mse + pow(array.get(_x,i) - array.get(_xhat,i),2)/_N
        _xmean = array.sum(_x)/_N
        _nrmse := sqrt(_mse) /_xmean
    _nrmse
    

diff(_src,_window,_degree) =>
    // Polynomial differentiator
    // input:
    // _src:: input series
    // _window:: integer: wigth of the moving lookback window
    // _degree:: integer: degree of fitting polynomial
    // output:
    // _diff :: series: time derivative
    // _nrmse:: float: normalized root mean square error
    //
    // Vandermonde matrix with implied dimensions (window x degree+1)
    // Linear form: J = [ [z]^0, [z]^1, ... [z]^degree], with z = [ (1-window)/2 to (window-1)/2 ] 
    var _J = array.new_float(_window*(_degree+1),0)
    for i = 0 to _window-1 
        for j = 0 to _degree
            matrix_set(_J,pow(i,j),i,j,_window)
    // Vector of raw datapoints:
    var _Y_raw = array.new_float(_window,na)
    for j = 0 to _window-1
        array.set(_Y_raw,j,_src[_window-1-j]) 
    // Calculate polynomial coefficients which minimize the loss function
    _C = pinv(_J,_window,_degree+1)
    _a_coef = multiply(_C,_Y_raw,_degree+1,_window,1)
    // For first derivative, approximate the last point (i.e. z=window-1) by 
    float _diff = 0.0
    for i = 1 to _degree
        _diff := _diff + i*array.get(_a_coef,i)*pow(_window-1,i-1)
    // Calculates data estimate (needed for rmse)
    _Y_hat = multiply(_J,_a_coef,_window,_degree+1,1)
    float _nrmse = norm_rmse(_Y_raw,_Y_hat)
    [_diff,_nrmse]

/// --- main ---
degree = input(title="Polynomial Order", group = "Model Parameters:",
              inline = "linepar1", type = input.integer, defval=2, minval = 1)
rsi_l = input(title = "RSI Length", group = "Model Parameters:", 
              inline = "linepar1", type = input.integer, defval = 21, minval = 1,
              tooltip="The period length of RSI that is used as input.")
window = input(title="Length ( > Order)", group = "Model Parameters:",
              inline = "linepar2", type = input.integer, defval=21, minval = 2)
signalLength = input(title="Signal Length", group = "Model Parameters:",
              inline = "linepar2", type=input.integer, defval=9,
              tooltip="The signal line is a EMA of the D-RSI time series.")
islong = input(title = "Buy", group = "Show Signals:",
              inline = "lineent",type = input.bool, defval = true)
isshort = input(title = "Sell", group = "Show Signals:",
              inline = "lineent", type = input.bool, defval= true)
showendlabels = input(title = "Exit", group = "Show Signals:",
              inline = "lineent", type = input.bool, defval= true)
buycond = input(title="Buy", group = "Entry and Exit Conditions:", 
              inline = "linecond",type = input.string, defval="Zero-Crossing", 
              options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
sellcond = input(title="Sell", group = "Entry and Exit Conditions:", 
              inline = "linecond",type = input.string, defval="Zero-Crossing", 
              options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
endcond = input(title="Exit", group = "Entry and Exit Conditions:", 
              inline = "linecond",type = input.string, defval="Zero-Crossing", 
              options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
usenrmse = input(title = "", group = "Filter by Means of Root-Mean-Square Error of RSI Fitting:", 
              inline = "linermse",type = input.bool, defval = false)
rmse_thrs = input(title = "RSI fitting Error Threshold, %", type = input.float, 
              group = "Filter by Means of Root-Mean-Square Error of RSI Fitting:",
              inline = "linermse", defval = 10, minval = 0.0) /100


src = rsi(close,rsi_l)
[drsi,nrmse] = diff(src,window,degree)
signalline = ema(drsi, signalLength)

// Conditions and filters
filter_rmse = usenrmse?nrmse<rmse_thrs:true
dirchangeup = (drsi>drsi[1]) and (drsi[1]<drsi[2]) and drsi[1]<0.0
dirchangedw = (drsi<drsi[1]) and (drsi[1]>drsi[2]) and drsi[1]>0.0
crossup = crossover(drsi,0.0)
crossdw = crossunder(drsi,0.0)
crosssignalup = crossover(drsi,signalline)
crosssignaldw = crossunder(drsi,signalline)

//Signals
golong = (buycond=="Direction Change"?dirchangeup:(buycond=="Zero-Crossing"?crossup:crosssignalup)) and  filter_rmse
goshort= (sellcond=="Direction Change"?dirchangedw:(sellcond=="Zero-Crossing"?crossdw:crosssignaldw)) and  filter_rmse
endlong = (endcond=="Direction Change"?dirchangedw:(endcond=="Zero-Crossing"?crossdw:crosssignaldw)) and filter_rmse
endshort= (endcond=="Direction Change"?dirchangeup:(endcond=="Zero-Crossing"?crossup:crosssignalup)) and filter_rmse
plotshape((golong and islong)  ? low : na, location=location.belowbar, style=shape.labelup,   color=#2E7C13,  size=size.small, title='Buy') 
plotshape((goshort and isshort) ? high: na, location=location.abovebar, style=shape.labeldown, color=#BF217C, size=size.small, title='Sell')
plotshape((showendlabels and endlong and islong)  ? high: na, location=location.abovebar, style=shape.xcross,   color=#2E7C13,  size=size.tiny, title='Exit Long') 
plotshape((showendlabels and endshort and isshort) ? low : na, location=location.belowbar, style=shape.xcross, color=#BF217C, size=size.tiny, title='Exit Short')

alertcondition(golong, title='Long Signal', message='D-RSI: Long Signal')
alertcondition(goshort, title='Short Signal', message='D-RSI: Short Signal')
alertcondition(endlong, title='Exit Long Signal', message='D-RSI: Exit Long')
alertcondition(endshort, title='Exit Short Signal', message='D-RSI: Exit Short')


if golong
    strategy.entry("Enter Long", strategy.long)
else if goshort
    strategy.entry("Enter Short", strategy.short)

---

• বোলিংজার ব্যান্ড এবং আরএসআই ইন্টিগ্রেশন সহ উন্নত গড় বিপরীতমুখী কৌশল
• সমর্থন/প্রতিরোধের সাথে মাল্টি-পিরিয়ড আরএসআই ডিভার্জেন্স
• ডায়নামিক ড্রাউনডাউন কন্ট্রোল সিস্টেমের সাথে অভিযোজিত প্রবণতা অনুসরণ কৌশল
• মাল্টি-টেকনিক্যাল ইন্ডিকেটর ক্রস-ট্রেন্ড ট্র্যাকিং কৌশলঃ আরএসআই এবং স্টোকাস্টিক আরএসআই সিনার্জি ট্রেডিং সিস্টেম
• ম্যাকডি-আরএসআই ক্রসওভার ট্রেন্ড বোলিংজার ব্যান্ডস অপ্টিমাইজেশন সিস্টেমের সাথে কৌশল অনুসরণ করে
• মাল্টি-ইন্ডিকেটর ডায়নামিক ট্রেডিং অপ্টিমাইজেশান কৌশল
• মাল্টি ইন্ডিকেটর ডায়নামিক স্টপ-লস ইম্পুটাম ট্রেডিং ট্রেন্ড কৌশল
• মাল্টি-ফিল্টার ট্রেন্ড ব্রুকথ্রু স্মার্ট মুভিং এভারেজ ট্রেডিং স্ট্র্যাটেজি
• জি-চ্যানেল সূচক সহ গতিশীল প্রবণতা গতি অপ্টিমাইজেশন কৌশল
• ইএমএ ক্রস স্ট্র্যাটেজি অনুসরণ করে একাধিক সূচক ট্রেন্ড
• মাল্টি-ইন্ডিকেটর ভোল্টেবিলিটি ট্রেডিং RSI-EMA-ATR কৌশল

---

• ডিমার্ক সেটআপ সূচক
• Bollinger Bands স্টোকাস্টিক RSI Extreme
• AK MACD BB INDICATOR V ১.০০
• প্যারাবোলিক এসএআর
• আরএসআই ডিভার্জেন্স ইন্ডিকেটর
• OBV MACD সূচক
• পিভট ট্রেন্ড
• মূল্য বৈষম্য কৌশল v1.0
• সাপোর্ট-রেসিস্ট্যান্স ব্রেকআউট
• ঢাল অনুকূলনামূলক চলমান গড়
• নিম্ন স্ক্যানার কৌশল ক্রিপ্টো
• [blackcat] L2 বিপরীত লেবেল কৌশল
• সুপার বি
• উচ্চ নিম্ন SAR
• সুপারট্রেক্স
• পিক ডিটেক্টর
• নিম্ন সন্ধানকারী
• এসএমএ ট্রেন্ড
• বোলিংজার সর্বনিম্ন
• সুপার ট্রেন্ড বি