Python, einfache Bayes-Anwendungen

Unter der Voraussetzung der gegenseitigen Unabhängigkeit der Variablen, die vorausgesagt werden, kann man nach dem Bayesian Theorem eine einfache Bayesian Klassifizierung erhalten. Ein einfacherer Ausdruck: Ein einfacher Bayesian Klassifikator nimmt an, dass eine Eigenschaft einer Klassifikation nicht mit anderen Eigenschaften dieser Klassifikation zusammenhängt. Zum Beispiel, wenn eine Frucht rund und rot ist und etwa 3 Zoll im Durchmesser ist, ist sie wahrscheinlich eine Apfel. Auch wenn diese Eigenschaften voneinander abhängen oder auf die Existenz anderer Eigenschaften angewiesen sind, wird ein einfacher Bayesian Klassifikator davon ausgehen, dass diese Eigenschaften jeweils unabhängig davon andeuten, dass die Frucht eine Apfel ist.

• Ein einfaches Bayes-Modell ist leicht zu konstruieren und sehr nützlich für große Datensätze. Obwohl es einfach ist, geht es bei einem einfachen Bayes-Modell über sehr komplexe Klassifikationsmethoden hinaus.

  Bayes' Theorem bietet eine Methode zur Berechnung der Nachprüfungswahrscheinlichkeit P (c) x aus P©, P (x) und P (x) c. Siehe folgende Gleichung:

  

  Hier, in der Stadt,

  P (c) x ist die nachträgliche Wahrscheinlichkeit einer Zielkategorie, wenn die Vorhersage der Variablen (Attribute) bekannt ist. P© ist die vorherige Wahrscheinlichkeit der Klasse P (x) c ist die Wahrscheinlichkeit, dass die Variablen, die vorausgesagt werden, unter der Annahme der bekannten Klasse stehen. P (x) ist die vorherige Wahrscheinlichkeit der vorhergesagten Variablen Beispiel: Lassen Sie uns mit einem Beispiel das Konzept verstehen. Nachfolgend habe ich eine Trainingssammlung für das Wetter und die entsprechende Zielvariable "Play-Play". Jetzt müssen wir die Teilnehmer, die spielen und nicht spielen, nach dem Wetter klassifizieren. Lassen Sie uns folgende Schritte ausführen.

  Schritt 1: Konvertieren Sie das Datensatz in eine Frequenztabelle.

  Schritt 2: Verwenden Sie eine ähnliche Wahrscheinlichkeit, wenn die Übercast-Wahrscheinlichkeit 0.29 ist und die Wahrscheinlichkeit des Spiels 0.64 ist, um eine Wahrscheinlichkeitstabelle zu erstellen.

  

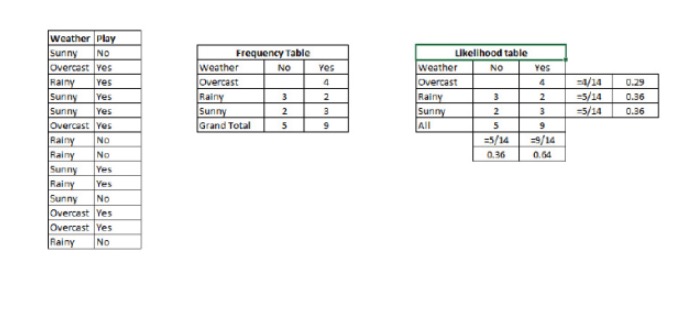
  Schritt 3: Jetzt berechnen Sie die Nachwahrscheinlichkeiten jeder Klasse mit den einfachen Bayes-Gleichungen. Die Klasse mit der größten Nachwahrscheinlichkeit ist das Ergebnis der Vorhersage.

  Frage: Wenn das Wetter schön ist, können die Teilnehmer spielen. Ist das richtig?

  Wir können das Problem mit der Methode lösen, über die wir gesprochen haben. Also P (spricht) = P (spricht) * P (spricht) / P (spricht)

  Wir haben P, das ist gleich 3/9 ist gleich 0.33, P, das ist gleich 5/14 ist gleich 0.36, und P, das ist gleich 9/14 ist gleich 0.64.

  Nun, P (wird spielen) = 0,33 mal 0,64 / 0,36 = 0,60, mit einer höheren Wahrscheinlichkeit.

  Ein einfacher Bayes verwendet eine ähnliche Methode, um die Wahrscheinlichkeit verschiedener Kategorien durch verschiedene Eigenschaften zu prognostizieren. Dieser Algorithmus wird häufig für die Klassifizierung von Texten und für Probleme mit mehreren Kategorien verwendet.

• Python-Code:

#Importieren von Bibliotheken von sklearn.naive_bayes importieren GaussianNB - Ich weiß. #Angenommen, Sie haben X (Predictor) und Y (Ziel) für den Trainingsdatensatz und x_test(Predictor) des Test_Datensatzes

Erstellen Sie ein SVM-Klassifizierungsobjektmodell = GaussianNB()

Es gibt eine andere Verteilung für Multinomial-Klassen wie Bernoulli Naive Bayes, Referenzlink

Training des Modells mit Hilfe der Trainingssätze und Prüfen der Punktzahl

model.fit(X, y) - Ich weiß. #Vorhersage der Ausgabe Vorhersage= Modell.Vorhersage ((x_test)