Bayesian classifier based on KNN algorithm

Bayesian classifier based on KNN algorithm

The theoretical basis for designing classifiers to make classified decisions:

Comparing P (ωi) x {\displaystyle P (ωi) x}; whereωi is class i, and x is a data to be observed and classified, P (ωi) x {\displaystyle P (ωi) x} represents the probability of determining that this data belongs to class i under the known characteristic vector, which also becomes the retrospective probability.

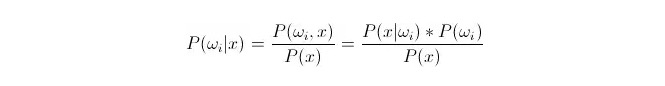
In this case, P (x) is called the likelihood or class-condition probability; P (ω) is called the prior probability because it is unrelated to the experiment and can be known before the experiment.

In classification, given x, the category that has the largest probability of P (ωi in x) can be selected. When P (ωi in x) is greater than P (ωi in x) in each category, ωi is a variable and x is a constant; so P (ωi in x) can be omitted and not taken into account.

So it comes down to the problem of calculating P (x) x (ωi) * P (ωi). Preliminary probability P (ωi) is desirable, as long as statistical training focuses on the proportion of data that appears under each classification.

The computation of the likelihood P (x) is a bit tricky because this x is the data in the test set and cannot be derived directly from the training set. Then we need to find the distribution law of the training set data to get P (x).

The following is an introduction to k neighbourhood algorithm, KNN.

We want to fit the distribution of these data under the category ωi based on the data x1, x2...xn in the training set (each of which is m-dimensional).

We know that when the data volume is large enough, we can use the proportional approximation probability. Using this principle, we find the k sample points nearest to the point x, which belong to category i. We calculate the volume V of the smallest supersphere surrounding this k sample point.

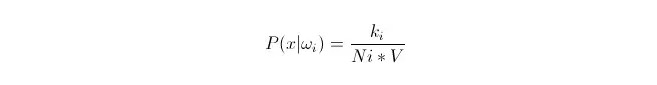
You can see that what we've calculated is actually the probability density of the class conditions at the point x.

So what's p (ωi)? According to the above method, P ((ωi) = Ni/N ⋅ where N is the total number of samples. In addition, P (x) = k/ (N*V), where k is the number of all sample points surrounding this supersphere; N is the total number of samples. Then we can compute P (ωi ∈ X): put the formula and it's easy to get:

P(ωi|x)=ki/k

In a V-shaped supersphere, there are k samples surrounded by ki of class i. Thus, we determine which class x should belong to if we have the most samples surrounded. This is a classifier designed with k adjacent algorithms.