Inventors describe the mechanism of quantitative analogue level retesting

Inventors describe the mechanism of quantitative analogue level retesting

• 1, the back-measurement architecture

  The inventor's quantified reticle strategy is a complete control process, where the program is continuously consulted at a certain frequency. The data returned by the various markets and trading APIs is also called at the time of the call, simulating the actual running situation. It belongs to the onTick level, not to the onBar level of other reticle systems.

• 2, Difference between analogue-level and real-dish level retesting

  • Simulated level retesting

    Analogue-level backtesting is the simulation of ticker data input values to this Bar in the time sequence of the underlying K-line data of the backtesting system, according to a certain algorithm in the framework of the numerical composition of the highest, lowest, opening and closing prices of the underlying K-line Bar.

  • Repeat at the real disk level

    Real disk-level retrieval is true ticker-level data in the time sequence of Bar. Using real disk-level retrieval is closer to true for ticker-level data-based strategies. The ticker is the actual data recorded, not the analogue generated.

• 3, analogue level retesting mechanism for the bottom K-line

  There is no underlying K-line option for real disk-level retesting (because ticker data is real and is not simulated using the underlying K-line). In analogue-level retrieval, a ticker is generated based on the K-line data; this K-line data is the bottom K-line. In actual use of analogue-level retrieval, the bottom K-line cycle must be smaller than the period of the API to obtain the K-line when the policy is running. Otherwise, due to the large number of tickers generated, the data will be truly lost when the API to obtain the specified period is called.

• 4 How the bottom K-line generates ticker data

  The underlying K-line generates analog tickers the same way as MT4.

  

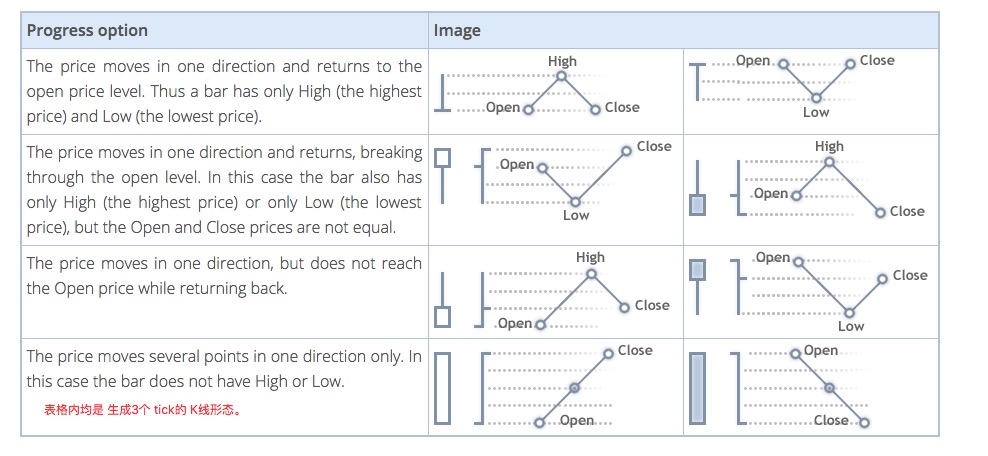
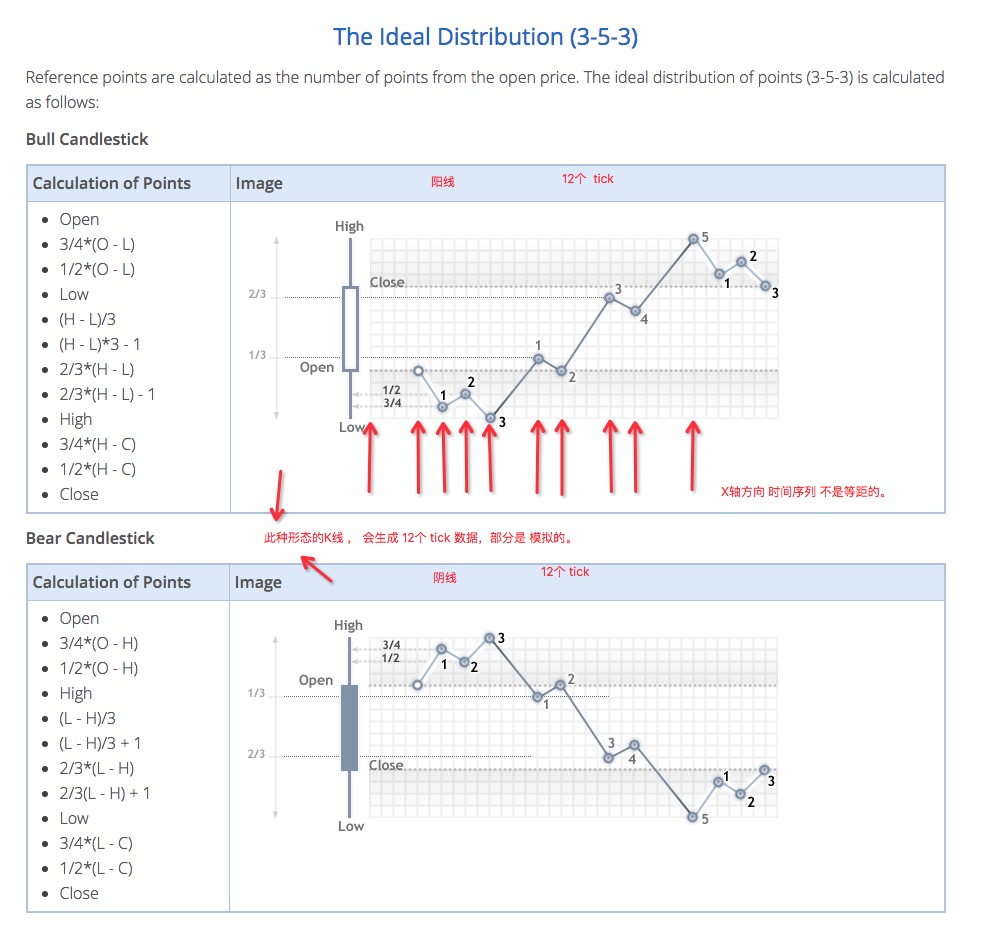
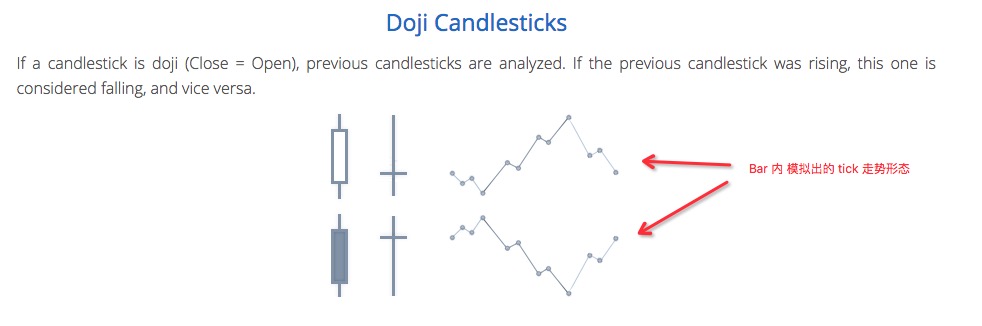
• 5, the algorithm code that generates ticker data

  A specific algorithm to simulate tick data from the bottom K-line data:

function recordsToTicks(period, num_digits, records) {
    if (records.length == 0) {
        return []
    }
    var ticks = []
    var steps = [0, 2, 4, 6, 10, 12, 16, 18, 23, 25, 27, 29]
    var pown = Math.pow(10, num_digits)

    function pushTick(t, price, vol) {
        ticks.push([Math.floor(t), Math.floor(price * pown) / pown, vol])
    }

    for (var i = 0; i < records.length; i++) {
        var T = records[i][0]
        var O = records[i][1]
        var H = records[i][2]
        var L = records[i][3]
        var C = records[i][4]
        var V = records[i][5]
        if (V > 1) {
            V = V - 1
        }
        if ((O == H) && (L == C) && (H == L)) {
            pushTick(T, O, V)
        } else if (((O == H) && (L == C)) || ((O == L) && (H == C))) {
            pushTick(T, O, V)
        } else if ((O == C) && ((O == L) || (O == H))) {
            pushTick(T, O, V / 2)
            pushTick(T + (period / 2), (O == L ? H : L), V / 2)
        } else if ((C == H) || (C == L)) {
            pushTick(T, O, V / 2)
            pushTick(T + (period * 0.382), (C == L ? H : L), V / 2)
        } else if ((O == H) || (O == L)) {
            pushTick(T, O, V / 2)
            pushTick(T + (period * 0.618), (O == L ? H : L), V / 2)
        } else {
            var dots = []
            var amount = V / 11
            pushTick(T, O, amount)
            if (C > O) {
                dots = [
                    O - (O - L) * 0.75,
                    O - (O - L) * 0.5,
                    L,
                    L + (H - L) / 3.0,
                    L + (H - L) * (4 / 15.0),
                    H - (H - L) / 3.0,
                    H - (H - L) * (6 / 15.0),
                    H,
                    H - (H - C) * 0.75,
                    H - (H - C) * 0.5,
                ]
            } else {
                dots = [
                    O + (H - O) * 0.75,
                    O + (H - O) * 0.5,
                    H,
                    H - (H - L) / 3.0,
                    H - (H - L) * (4 / 15.0),
                    H - (H - L) * (2 / 3.0),
                    H - (H - L) * (9 / 15.0),
                    L,
                    L + (C - L) * 0.75,
                    L + (C - L) * 0.5,
                ]
            }
            for (var j = 0; j < dots.length; j++) {
                pushTick(T + period * (steps[j + 1] / 30.0), dots[j], amount)
            }
        }
        pushTick(T + (period * 0.98), C, 1)
    }
    return ticks
}

Therefore, when using analogue-level retracement, there is a price jump in the time sequence.