Support vector machines in the brain

Support vector machines in the brain

Support vector machine (SVM) is an important machine learning classifier that cleverly uses non-linear transformations to project low-dimensional features into high-dimensional ones to perform more complex classification tasks (up-dimensional knocks). SWM seems to use a mathematical gimmick that just happens to match the mechanisms of brain coding, as we can read from a 2013 Nature paper that the surface connection between understanding deep machine learning and how the brain works is the use of machine learning to study the brain. The importance of mixed selectivity in complex cognitive tasks (by Omri Barak al.)

• SVM

  The first process is called encoding, the second process is called decoding, and the real purpose of neural encoding is to decode the decision. So, using machine learning's visual code, the easiest way to do it is to use a classifier, or even a logistic model, a linear classifier, which treats the input signals according to certain characteristic categories.

  So let's see how the neural coding works, first of all, the neuron can basically be thought of as an RC circuit that adjusts the resistance and capacitance according to the external voltage, if the external signal is large enough, it conducts, otherwise it closes, and represents a signal by the frequency of discharge in a certain time. And we talk about coding, often doing a discrete processing of time, assuming that in a small time window, this rate of discharge is constant, so that a neural network in this time window the rate of discharge of cells in this time window can be seen together as a N-dimensional quantity, N is the individual neuron, this N-dimensional quantity, we call it the coding numerator, it can express the image of the animal seen, or the sound heard, which will cause the corresponding external-expression of the neural cortex network.

  

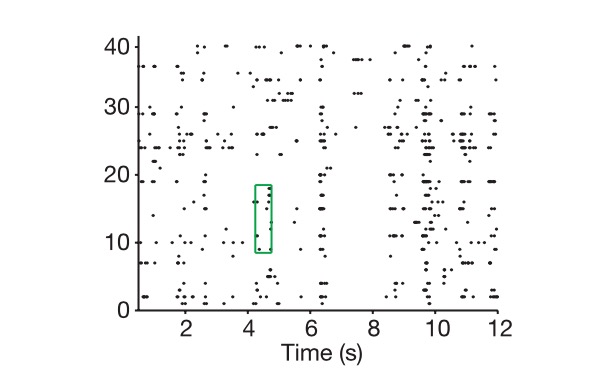
  Graph: The longitudinal axis is the cell, the horizontal axis is the time, and the graph shows how we extract the neural code.

  First, we enter this N-dimensional space labeled by the N-dimensional vector, and then we give all possible combinations of tasks, such as showing you a thousand images assuming these images represent the whole world, marking each time we get the neural code as a point in this space, and finally we use vector algebraic thinking to see the dimension of the subspace that this thousand points make up, which is defined as the true dimension of the neural representation. I assume that all points are actually on a piece of this N-dimensional space, so this representation is one-dimensional, which is equivalent to if all points are on a two-dimensional side of a high-dimensional space, then it is two-dimensional.

  In addition to the real dimension of coding, we have a concept of the real dimension of the external signal, where the signal refers to the external signal expressed by the neural network, and of course you have to repeat all the details of the external signal. It is an infinite problem, however, our classification and decision-making is always based on the key characteristics, a process of reduction, which is also the idea of PCA. We can think of the key variables in the real task as the real dimension of the task.

  So scientists are faced with a core question, why solve this problem with a coding dimension and a number of neurons that are much higher than the real problem?

  And computational neuroscience and machine learning together tell us that the high-dimensional properties of neural representations are the foundation of their strong university learning ability. The higher the coding dimension, the stronger the learning ability. Notice that we're not even getting into deep networks here. Why do we say that?

  Note that the neural coding discussed here refers mainly to the neural coding of the higher neuronal centers, such as the prefrontal cortex (PFC) discussed in this article, since the coding rules of the lower neuronal centers are not so much about classification and decision-making.

  

  The PFC represents the higher brain region

  The mystery of neural coding is also revealed from the relationship between the number of neurons N, and the dimension K of the real problem (this gap can be up to 200 times). Why does a seemingly redundant number of neurons lead to a qualitative leap? First, we assume that when our coding dimension is equal to the dimension of the key variable in the real task, we will not be able to handle nonlinear classification problems using a linear classifier (assuming that you are going to separate squid from squid, you cannot remove squid from squid with a linear boundary), which is also a typical problem we have difficulty solving in deep learning and when the SVM does not enter machine learning.

  SVM (supports vector machines):

  

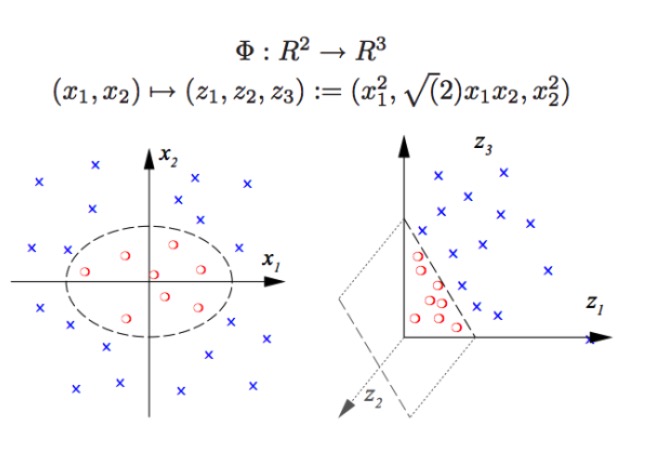
  SVM can do non-linear classification, such as separating the red and blue points in a graph, and using a linear boundary we are unable to separate the red and blue points ((left graph), so the way to use SVM is to raise the dimension. It is not possible to simply increase the number of variables, such as mapping ((x1, x2) to ((x1, x2, x1+x2) systems, which are actually two-dimensional linear spaces ((graph is a red point and a blue point on a plane), only using the non-linear function ((x1^2, x1*x2, x2^2) we have a substantive low-dimensional to high-dimensional crossover, in which case you just throw the blue point into the air, and then you just draw a point in the space, dividing the blue plane and the red point on the right graph.

  In fact, what a real neural network does is exactly the same thing. The sort of sorting that a linear classifier (decoder) can do is greatly increased, meaning that we have a much stronger pattern recognition ability than before.

  So, how do we get high-dimensional coding of neurons? More optical neurons are useless. Because we have learned linear algebra, we know that if we have a large number of N neurons, and the rate of discharge of each neuron is only linearly related to a key characteristic K, then our final expression dimension will only be equal to the dimension of the problem itself, and your N neurons will have no effect.

  

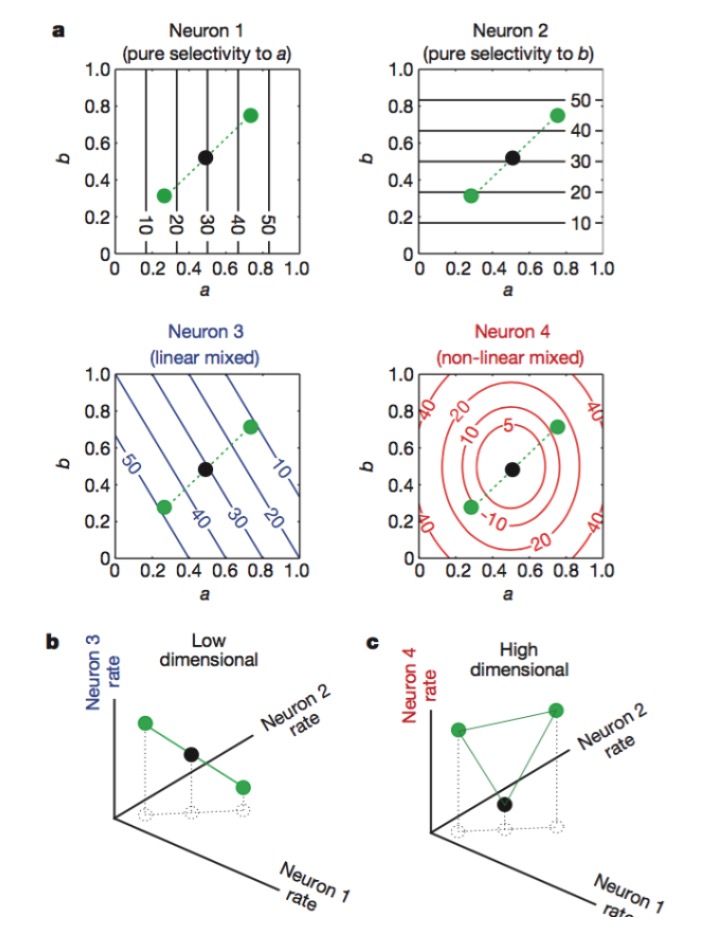
  Figure 1: Neurons 1 and 2 are sensitive only to features a and b, respectively, 3 are sensitive to a linear mixture of features a and b, and 4 are sensitive to a nonlinear mixture of features. In the end, only the combination of neurons 1, 2, and 4 increases the dimension of neural coding.

  The official name for this type of coding is mixed selectivity, which we find incomprehensible until the principle of this coding has been discovered, because it is a neural network that responds to a signal in a messy way. In the peripheral nervous system, neurons act as sensors to extract and recognize patterns of different characteristics of the signal. Each neuron has a rather specific function, such as rods and cones in the retina, which are responsible for receiving photons, and then continue to be coded by the original ganglion cell, each neuron is like a professionally trained sentinel.

  Every detail of nature is hidden in a maze, a lot of redundancy and mixed coding, this seemingly unprofessional approach, seemingly messy signals, ultimately result in better computing power.

  

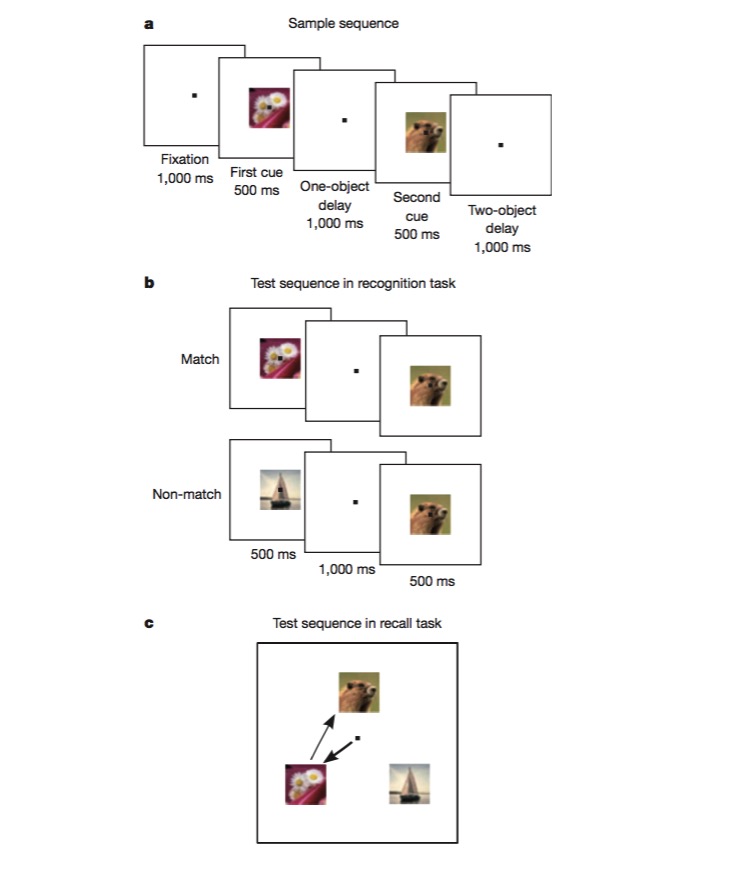
  In this task, the monkey is first trained to recognize if an image is the same as the previous one, and then trained to judge the order in which two different images appear (recall). The monkey must be able to code for different sides of the task, such as task type (recall or recognition), image type, etc., and this is an excellent test of whether mixed non-linear coding mechanisms exist. Experiments have shown that a large number of neurons are sensitive to mixed features, and that there are non-linear ones (e.g. the same is done with flower coding, the intensity of neuronal release depends on whether the task is recall or recognition, not independent of the characteristics).

  After reading this article, we realized that designing a neural network would greatly improve pattern recognition if some non-linear units were introduced, and that the SVM just happened to apply this to solve the non-linear classification problem.

  We study the function of brain regions, first processing data using machine learning methods, such as finding key dimensions of problems with PCA, then understanding neural coding and decoding with machine learning pattern recognition thinking, and finally, if we get some new inspiration, we can improve the machine learning method. For the brain or machine learning algorithms, the ultimate thing is to get the most appropriate representation of the information, and with the right representation, everything is easy. This is where machine learning returns from linear logic to support a step-by-step evolutionary process of quantum machine learning, or maybe this is also where the brain evolves, and we have an ever-increasing control over the world.

Translated from the Chinese by Xue Xue Iron-Cruiser Technology