Python and the Simple Bayes Application

A simple Bayesian classifier assumes that a property of a classification is unrelated to other properties of that classification. For example, if a fruit is round and red and about 3 inches in diameter, it is likely to be an apple. Even if these properties are interdependent or dependent on each other, a simple Bayesian classifier assumes that these properties independently imply that the fruit is an apple.

• Simple Bayesian models are easy to construct and are very useful for large data sets. Although simple, simple Bayesian representations go beyond very complex classification methods.

  Bayes' theorem provides a method for calculating the probability of a consequence P (c) from P©, P (x) and P (x) c. See the following equation:

  

  Here, we have a video.

  P (c) x is the probability of a subsequent event of the class (target) on the premise that the predictive variable (attributes) are known P© is the prior probability of the class P (x) c is the probability, i.e. the probability of predicting a variable under the assumption of a known class P (x) is the prior probability of the predicted variable Example: Let's understand the concept with an example. Below, I have a training set for weather and the corresponding target variable, the Play button. Now, we need to classify the participants who will be playing and those who will not be playing based on the weather. Let's perform the following steps.

  Step 1: Convert the dataset to a frequency table.

  Step 2: Create a likelihood table using a likelihood of overcast 0.29 and a likelihood of playing 0.64 when the likelihood of overcast is 0.29

  

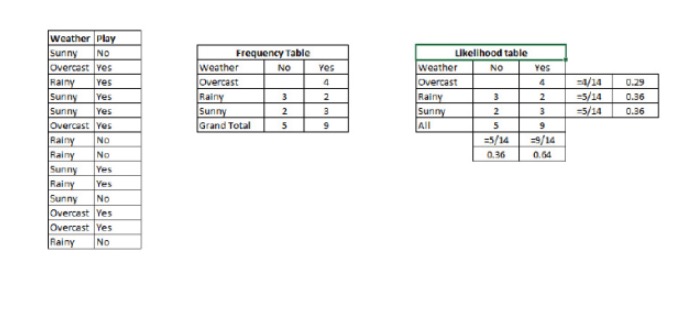
  Step 3: Now, use the plain Bayesian equation to calculate the probability of each class; the class with the largest probability of the class is the result of the prediction.

  Question: If the weather is nice, the participants can play. Is this statement correct?

  We can solve this problem using the method we discussed earlier. So P (playing) = P (playing) * P (playing) / P (playing)

  So we have P (play) = 3/9 is 0.33, P (play) = 5/14 is 0.36, P (play) = 9/14 is 0.64.

  Now, p (will play) is equal to 0.33 times 0.64 / 0.36 is 0.60, with a higher probability.

  The naive Bayes uses a similar method to predict the probabilities of different categories using different properties. This algorithm is commonly used for text classification, as well as for problems involving multiple categories.

• Python code:

#Import Library from sklearn.naive_bayes import GaussianNB 　　 #Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset

Create SVM classification object model = GaussianNB()

there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link

Train the model using the training sets and check score

model.fit(X, y) 　　 #Predict Output predicted= model.predict(x_test)