Visualizing modules to build trading strategies - in depth

Visualization modules build trading strategies in depth

• Type of logic module

  • The first condition module

    The module is used for combination condition judgments, and the module can add multiple condition branches. Click on the little "turbine" icon to add the condition branch.

    

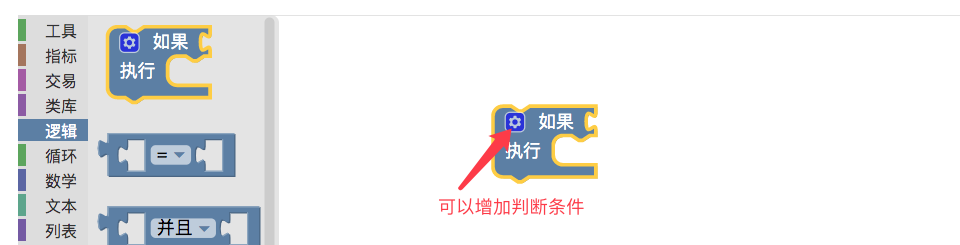
    Use cases for conditional modules We combine the tests with the next module.

  • 2, the numerical comparison module

    The module is used to compare two numerical values (also considered a composite expression module) and returns a Boolean value. The module can determine the numerical values of the two sides: is greater than , is less than , is greater than or equal to , is less than or equal to , is not equal to , is equal to . Both sides of the drop-down options can be embedded with a value, variable module (if the module returning the value can be embedded).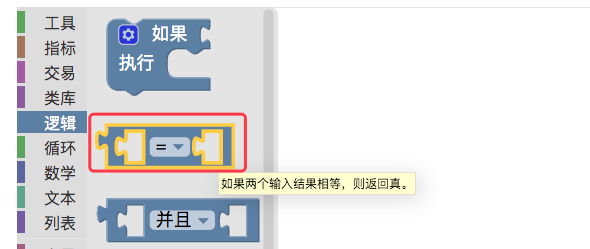

    

    An example of a numerical determination using a "conditional module" and a "comparison module" is given below:

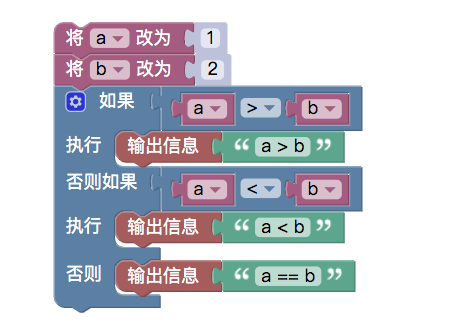    As you can see, this paradigm has three branches when it comes to judging conditions.

    For example, the use of the if statement in JavaScript policy.

    function main () {
        var a = 1
        var b = 2
        if (a > b) {
            Log("a > b")
        } else if (a < b) {
            Log("a < b")
        } else {
            Log("a == b")
        }
    }
    

  • 3, logical or, logical and modular

    This module is used to perform a loop or operation loop or a loop and operation loop, with the option to drag the middle of the module to the left and right of the loop. The loop is embedded in the module involved in the operation.

    

    Before we test this module specifically, we first learn that the module that represents the Boolean value is a true/false Boolean module (set using the pull-down box), the module that represents the Boolean value is a non-boolean module, and the module that represents the empty value.

    

    • The empty module, which represents thenullValue, used to compare whether some variables are empty.
    • The module of the true/false boolean is the one that represents the value in the code.true / falseA value used to determine the Boolean value returned by some module or combination of modules.
    • The boolean value is the non-volatile module that represents the code.!, which is used for non-Boolean operations.

    This is a test case:

    

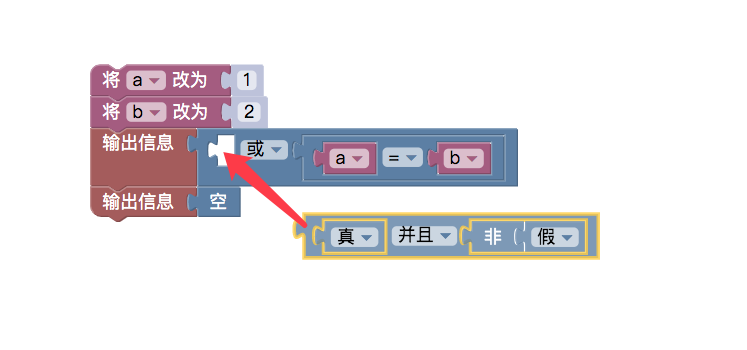
    You can see that "logic" or "logical and" modules can also be used in nested mode.

    An example of nested module splicing:

    

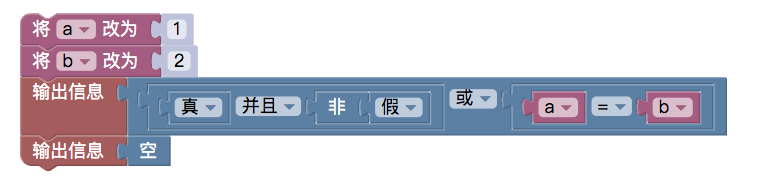
    The equivalent JavaScript policy code is:

    function main () {
        var a = 1 
        var b = 2
        Log((true && !false) || (a==b))
        Log(null)
    }
    

    !false for non-false, i.e. true, logical expression: ((true & &!false): two true values are performed and computed, resulting in true. a==b is obviously not equal, so it is false. A true value and a false value are logically or operationally evaluated and the result is true.

    The results:

  • 4, three-dimensional operating modules

    The module is also known as the assertion module, and functions similarly to the three-dimensional operator in some programming languages.

    

    This module can also be used in nested mode, and the three-dimensional operating module is similar in nature to the conditional logic, function and conditional module.

    The teaching example of the "conditional module" in the above text is reconstructed using three-dimensional operating modules. The following examples:

    

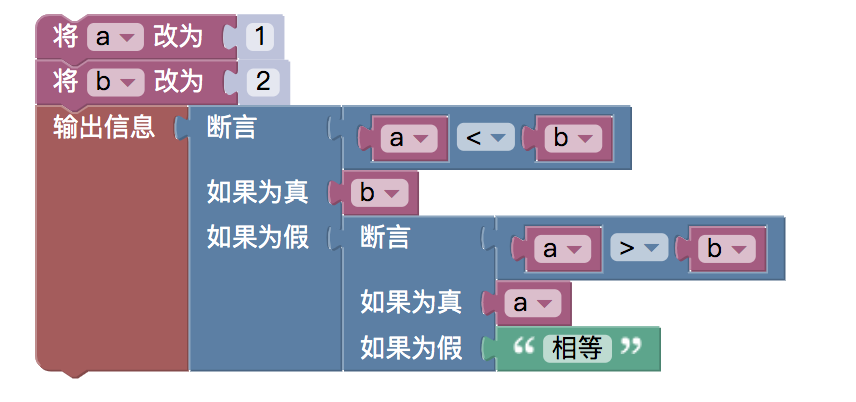
    For example, the policy code written in JavaScript:

    function main () {
        var a = 1
        var b = 2
        Log(a < b ? b : (a > b ? a : "相等"))
    }
    

    Interestingly, we can adjust the value of a ⋅ b to run the retest.

• Math module types

  In many of the previous examples, we used more or less mathematical modules. Below we explain some of the modules that you haven't learned yet.

  • 1, the trigonometric function module

    Note that the parameters for the position of the module () are angular values, not arc values.

    

  • 2, roundness of the numerical module

    

    Re-test the print:

  • 3, take a random number module within a given range of values

    The module takes a random number within a range of values set, and the module can fill in a value directly from the position of the "" or use a variable as the start and end values of the random range.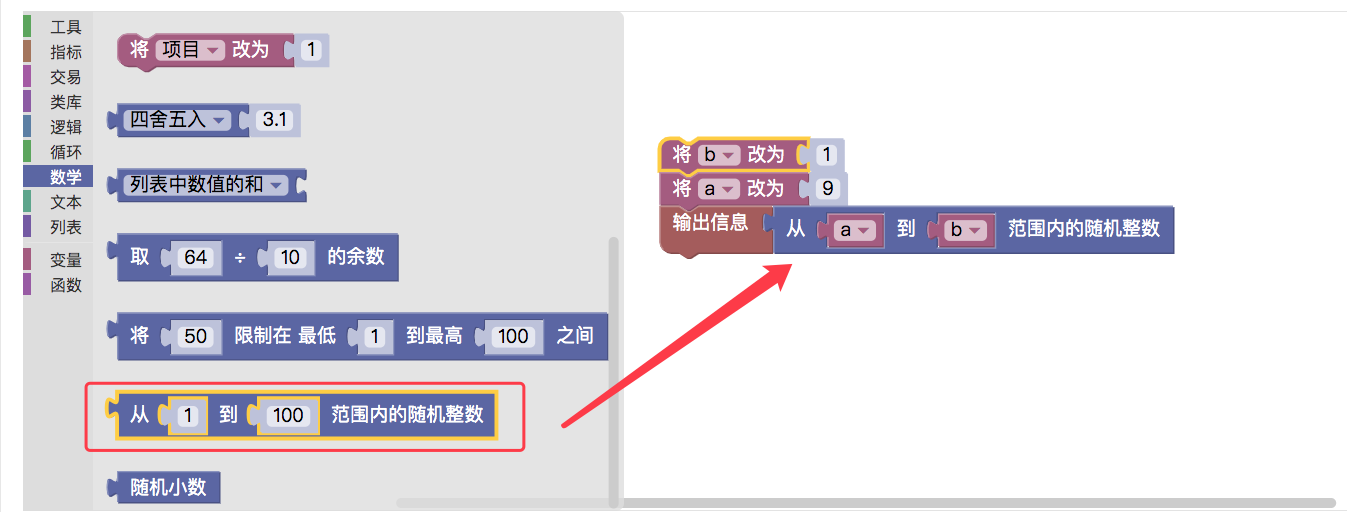

    

    For example, JavaScript policy code:

    function main () {
        var a = 1
        var b = 9
        Log(_N(a + Math.random() * (b - a), 0))
    }
    

  • 4, Module with limiting range

    The module restricts the filling of variables in the first and second positions to the range of values set in the second and third positions. If the maximum value of the range is greater than this, the module returns the maximum value of the range, and if the minimum value of the range is less than this, the module returns the minimum value. If within this range, the value of the variable itself is returned if the value of the first () is taken.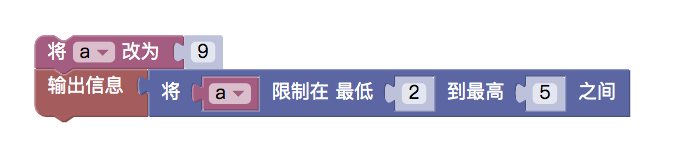

    

    For example, JavaScript policy code:

    function main () {
        var a = 9
        Log(Math.min(Math.max(2, a), 5))
    }
    

  • 5 and the remaining modules

    The module performs a numerical surplus operation on the value module set to the position of the ().

    

    64 divided by 10 is 6 plus 4⁄4.

  • 6, the list operation module

    This module performs operations on a list module (e.g. calculating the sum of elements in the list).

    

    

    For example, JavaScript policy code:

    function sum (arr) {
        var ret = 0
        for (var i in arr) {
            ret += arr[i]
        }
        return ret 
    }
    
    function main () {
        var b = 2
        var a = 1
        Log(sum([b,a,b,a,a]))
    }
    

Visualizing the paradigm strategy:

• https://www.fmz.cn/strategy/121404
• https://www.fmz.cn/strategy/129895
• https://www.fmz.cn/strategy/123904
• https://www.fmz.cn/strategy/122318

More tips can be found at:https://www.fmz.cn/square

Other articles in this series

• Visualizing modules to build trading strategies - progress
• Visualizing modules to build trading strategies - a basic understanding

It's boring programming, it's easy to do with blocks, try it out, it's fun!