Clasificador bayesiano basado en el algoritmo KNN

La base teórica para el diseño de clasificadores para tomar decisiones de clasificación:

Comparación P(ωi 173xxx) ⋅ donde ωi es de clase i y x es un dato observado y clasificado, P(ωi 173xxx) representa la probabilidad de determinar que el dato pertenece a la clase i en el caso de que se conozca el vector de características de este dato, que también se convierte en la probabilidad posterior. Según la fórmula de Bayes, se puede representar como:

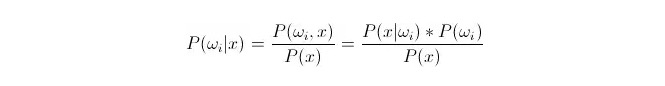
De ellos, P (x) {\displaystyle \mathrm {P} (x) } se llama probabilidad de semejanza o probabilidad de clase; P (ω) {\displaystyle \mathrm {P} (i) } se llama probabilidad previa, ya que no tiene que ver con el experimento y se conoce antes del experimento.

En la clasificación, dado x, se puede elegir la categoría que hace que la probabilidad de posterioridad P ((ωiⴰⵙx) sea la mayor. En la comparación de cada categoría, cuando P ((ωiⴰⵙx) es pequeña, ωi es variable y x es constante; por lo tanto, se puede eliminar P ((x) sin tenerla en cuenta.

Así que lo que se reduce a es P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x) = P (x).*P ((ωi) de la pregunta La probabilidad previa P ((ωi) es buena, siempre y cuando el entrenamiento estadístico se centre en la proporción de datos que aparecen en cada clasificación.

La probabilidad de que P (x < i < i) sea el resultado de la prueba es muy complicada, ya que x es el resultado de la prueba y no se puede obtener directamente del conjunto de entrenamiento. Entonces necesitamos encontrar la ley de distribución de los datos del conjunto de entrenamiento y obtener P (x < i < i < i) < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i < i > .

A continuación se presenta el algoritmo de cercanía k, en inglés KNN.

Se trata de la distribución de los datos x1, x2…xn (en los que cada dato es m-dimensional) de la concentración de entrenamiento, en la categoría ωi. Si x es un punto arbitrario en el espacio m-dimensional, ¿cómo se calcula P ((x y ωi)?

Sabemos que cuando la cantidad de datos es lo suficientemente grande, se puede usar una aproximación proporcional a la probabilidad. Utilizando este principio, en el entorno del punto x, encuentre los puntos de la muestra más cercanos a la distancia del punto x, de los cuales alguno pertenece a la categoría i. Calcule el volumen V de la superesfera más pequeña que rodea a estos puntos de la muestra k; y encuentre el número de Ni que pertenece a la clase ωi en todos los datos de la muestra:

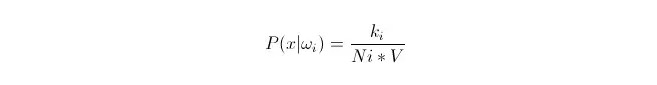
Y como se puede ver, lo que hemos calculado es en realidad la densidad de probabilidad de clase en el punto x.

¿Qué pasa con P (ωi)? De acuerdo con el método anterior, P ((ωi) = Ni/N 。 donde N es el número total de muestras。 Además, P (x) = k/N.*V), donde k es el número de todos los puntos de la muestra que rodean este súper globo; N es el número total de muestras. Entonces P (ωi kesinx) puede ser calculado como:

P(ωi|x)=ki/k

En una superesfera de tamaño V, rodeamos k muestras, de las cuales hay ki pertenecientes a la clase i. De esta manera, de las muestras más rodeadas, podemos determinar a qué clase debería pertenecer x. Este es el clasificador diseñado con el algoritmo de proximidad k.