Aplicaciones de Python y Bayes

Se obtiene el método de clasificación de Bayes por el teorema de Bayes basado en la presunción de la independencia de las variables predictivas. En palabras más simples, un clasificador de Bayes presupone que una característica de una clasificación no está relacionada con otras características de esa clasificación. Por ejemplo, si una fruta es red y redonda y tiene un diámetro de aproximadamente 3 pulgadas, es probable que sea una manzana. Incluso si estas características dependen una de la otra o dependen de la existencia de otras características, el clasificador de Bayes presupone que estas características indican que la fruta es una manzana.

• Los modelos Bayesian simples son fáciles de construir y son muy útiles para grandes conjuntos de datos. Aunque son simples, los comportamientos de Bayesian simples van más allá de métodos de clasificación muy complejos.

  El teorema de Bayes proporciona un método para calcular la probabilidad de posterior experimentación P (c) x a partir de P©, P (x) y P (x) c. Consulte la siguiente ecuación:

  

  En este lugar,

  P (c) es la probabilidad posterior de la clase (objetivo) con la condición de que se conozca la variable predictiva (propiedad). P© es la probabilidad previa de la clase P (x ∈ c) es la probabilidad, es decir, la probabilidad de una variable predictiva bajo una clase conocida. P (x) es la probabilidad previa de una variable predictiva. Ejemplo: Vamos a entender el concepto con un ejemplo. A continuación, tengo un conjunto de entrenamiento de clima y la variable de objetivo correspondiente Play Play. Ahora, necesitamos clasificar a los participantes de la reunión que están jugando y los que no están jugando según el clima. Vamos a realizar los siguientes pasos.

  Paso 1: Convierta el conjunto de datos en una tabla de frecuencia.

  Paso 2: Utiliza una tabla de probabilidad similar a la tabla de probabilidad de juego, como la tabla de probabilidad de 0.64 cuando la probabilidad de Overcast es de 0.29.

  

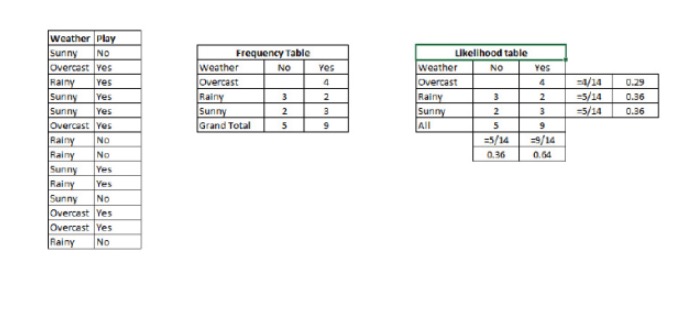
  Paso 3: Ahora, utilice las ecuaciones simples de Bayes para calcular la probabilidad posterior de cada clase. La clase con mayor probabilidad posterior es el resultado de la predicción.

  Pregunta: Si el tiempo es bueno, los participantes pueden jugar. ¿Es esta declaración correcta?

  Podemos resolver este problema usando el método que hemos discutido. Así que P (Jugará) = P (Jugará) * P (Jugará) / P (Jugará)

  Así que tenemos P = 3/9 = 0.33, P = 5/14 = 0.36, P = 9/14 = 0.64.

  Ahora, P (que jugará) = 0.33 * 0.64 / 0.36 = 0.60, con una mayor probabilidad.

  Por lo general, Bayes usa un método similar para predecir las probabilidades de diferentes categorías a través de diferentes propiedades. Este algoritmo se utiliza para clasificar el texto, así como para problemas que involucran varias categorías.

• El código de Python:

#Importar biblioteca desde sklearn.naive_bayes importar GaussianNB - ¿ Qué? # Suponiendo que tiene, X (predictor) y Y (objetivo) para el conjunto de datos de entrenamiento y x_test ((predictor) de test_dataset

Crear el modelo de objeto de clasificación SVM = GaussianNB()

hay otra distribución para clases multinomiales como Bernoulli Bayes ingenuo, enlace de referencia

Entrenar al modelo utilizando los conjuntos de entrenamiento y comprobar la puntuación

model.fit(X, y) - ¿ Qué? #Predecir el resultado predicted= modelo.predict ((x_test))