sommets et latitudes

sommets et latitudes

• Le point de vue de la courtoisie et de la skewness

  Il y a un problème avec le système bancaire.

  Il s'agit d'une stratégie de trading appliquée à la courtosis et à la skewness de la distribution des données statistiques. Nous faisons plus lorsque les données sont tendance et que les tendances potentielles sont positives. Nous faisons un vide lorsque les données sont tendance et que les tendances potentielles sont négatives.

  Alors, comment déterminer la tendance et l'intensité de la tendance?

  Tout d'abord, la définition de la distribution normale.

  Distribution: cas de répartition où toutes les valeurs des variables apparaissent plusieurs fois, représenté par les valeurs des variables sur l'axe horizontal et les coordonnées de fréquence sur l'axe longitudinal. Distribution normale: aussi appelée distribution de Gauss.

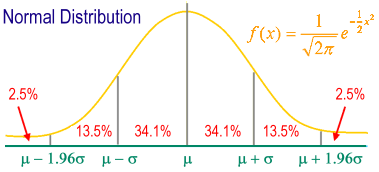
  Distribution normale standard: diagramme de la distribution normale dessiné en unité de base de l'axe de coordonnées avec le déviation standard centrée sur la moyenne.

  M ± 1 s contient 68.26% des individus de l'ensemble du groupe d'échantillons.

  M ± 2 s contient 95.44% des individus de l'ensemble du groupe d'échantillons.

  M ± 3 s contient 99,74% des individus de l'ensemble du groupe d'échantillons.

  95% des individus tombent entre m ± 1.96 s.

  99% des individus tombent entre m ± 2.58 s.

  

  En statistique, la courtoisie mesure le pic de la distribution des probabilités des variables aléatoires réelles.

  La courtoisie est la mesure de la concentration de la distribution d'un ensemble de données. La courtoisie de la distribution normale est de 3, donc nous appelons la courtoisie de plus de 3 pour indiquer que la distribution est plus concentrée et plus calme que la distribution normale. Nous appelons la courtoisie de moins de 3 pour indiquer que la distribution est plus lisse que la distribution normale. Nous parlons ici de la courtoisie réelle moins la valeur de 3.

  La skewness dépeint la symétrie de la distribution des données, ou la position des modes; la skewness égale à 0 dépeint la symétrie parfaite. Cette statistique nécessite également une comparaison avec la distribution normale: une skewness supérieure à 0 indique que l'array se présente à droite par rapport à la distribution normale, qui se présente comme une longue queue à droite et dont les extrêmes sont plus largement dispersés à droite; une skewness inférieure à 0 peut être expliquée par une tendance à la baisse de la tendance des données vers l'accumulation.

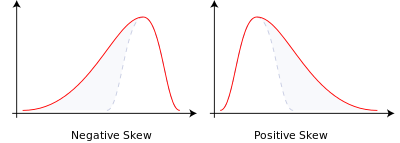
  En probabilité et en statistique, le biais mesure l'asymétrie de la distribution des chances des variables réelles aléatoires. Les valeurs du biais peuvent être positives, négatives ou même indéfinissables. Quantitatifs, le biais négatif signifie que la queue sur le côté gauche de la fonction de densité de probabilité est plus longue que celle sur le côté droit, et que la majorité des valeurs (y compris les moyennes) se trouvent à droite de la moyenne. Le biais positif signifie que la majorité des valeurs moyennes (y compris les moyennes) se trouvent à gauche de la moyenne.

  Le parti pris est divisé en deux catégories:

  • Bias négatif ou bias gauche: la queue est plus longue sur le côté gauche et le sujet principal de la distribution est concentré sur le côté droit.
  • Paradoxalement, la position de l'animal à droite est plus longue que la position de la queue à droite, et la position de l'animal à gauche.
  • Si la distribution est symétrique, alors la moyenne = le nombre moyen, la déviation est nulle (en outre, si la distribution est une distribution monocamérale, alors la moyenne = le nombre moyen = le nombre de nombres).

  

• Nous avons donc déduit les règles de négociation suivantes: Lorsque le pic est inférieur à 0 (le marché est dans un marché tendance), le décalage est supérieur à N (le marché tendance est à la hausse), faites plus; Lorsque le pic est inférieur à 0 (le marché est dans un marché tendance), le décalage est inférieur à M (la tendance est à la baisse), faire le vide;

MATLAB source code: Les tests intéressants peuvent être convertis en JS.

input:ExitType(5) ;
input:NBarL(2),NBarS(2),TradeProfit(0.053),TradeStopLoss(0.023),ATRs_L(5.4),ATRs_S(10.9);
vars: IsBalanceDay(False),MP(0),PF(0),PL(0),HLRange(100);

inputs:Length(20),Trigger(3),UpSkew(3.4),DownSkew(2.2) ;
vars:KurtValue(0),SkewValue(0),BuyPoint(0),SellPoint(0);

MP = MarketPosition ;
if DAYofMonth(Date) > 14 and DAYofMonth(Date) < 22 and DAYofWeek(Date)= 3 then isBalanceDay = True else isBalanceDay =False ;

PF = AvgPrice*TradeProfit ;
PL = AvgPrice*TradeStopLoss ;

{计算峰度 }
KurtValue = Kurtosis(Close,Length) ;
{计算偏度}
SkewValue = Skew(Close,Length) ;

{ 峰度向下跌破 Trigger 线 ,建立买卖点 }
if KurtValue Cross under Trigger then Begin
BuyPoint = High 3;
SellPoint = Low-3;
end;

{ 偏度大于某数值后 ,趋势确认进场作多 }
if  SkewValue > -UpSkew 2 then Buy next bar at BuyPoint stop ;
{ 偏度小于某数值后 ,趋势确认进场作空 }
if  SkewValue < -DownSkew 2 then Sell next bar at SellPoint Stop ;
end;

if ExitType = 1 then SetStopLoss(PL * BigPointValue) ;

if ExitType = 2 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
end;

if ExitType = 3 then Begin
if MP > 0 and BarsSinceEntry = NBarL then ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then ExitShort next bar at Market ;
end;

if ExitType = 4 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
if MP > 0 and BarsSinceEntry = NBarL then {Sell } ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then {Buy} ExitShort next bar at Market ;
end;

if ExitType = 5 then Begin
{*******************************************************************
Description : ATR Trailing Stop Long Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
********************************************************************}
{Inputs: ATRs_L(3);}
Variables: PosHigh(0), ATRVal_L(0);

ATRVal_L = AvgTrueRange(10) * ATRs_L;
If BarsSinceEntry = 0 Then PosHigh = High;
If MarketPosition = 1 Then Begin
If High > PosHigh Then PosHigh = High;
ExitLong ("ATR") Next Bar at PosHigh - ATRVal_L Stop;
End else ExitLong ("ATR eb") Next bar at High - ATRVal_L Stop;

{*******************************************************************
Description : ATR Trailing Stop Short Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
******************************************************************}
{Inputs: ATRs_S(3);}
Variables: PosLow(0), ATRVal_S(0);

ATRVal_S = AvgTrueRange(10) * ATRs_S;
If BarsSinceEntry = 0 Then PosLow = Low;
If MarketPosition = -1 Then Begin
If Low < PosLow Then PosLow = Low;
ExitShort ("ATR_1") Next Bar at PosLow ATRVal_S Stop;
End else ExitShort ("ATR_1 eb") Next bar at Low ATRVal_S Stop;
end;

if IsBalanceDay then setExitonClose ;

Il a été publié par le blogue de Faruto