Python, une application Bayesian simple

On obtient la méthode de classification de Bayes le plus simple selon le théorème de Bayes. En termes plus simples, un classificateur de Bayes le plus simple suppose qu'une caractéristique d'une classification n'est pas liée à d'autres caractéristiques de cette classification. Par exemple, si un fruit est rond et rouge et a un diamètre d'environ 3 pouces, il est probable que ce soit une pomme.

• Les modèles Bayesian simples sont faciles à construire et très utiles pour les grands ensembles de données. Bien que simples, les performances des modèles Bayesian simples vont au-delà des méthodes de classification très complexes.

  Le théorème de Bayes fournit une méthode pour calculer la probabilité d'expérience ultérieure P (c) x à partir de P©, P (x) et P (x). Voir l'équation suivante:

  

  Il y a des gens qui sont là.

  P (c) est la probabilité postérieure d'une classe (objectif) sous réserve d'une variable (attribut) de prédiction connue P© est la probabilité antérieure de la classe P (x) c est la probabilité, c'est-à-dire la probabilité, d'une variable prédite dans une classe connue. P (x) est la probabilité antérieure de la variable annoncée. Exemple: pour comprendre ce concept, nous allons utiliser un exemple. Ci-dessous, j'ai un ensemble de formation sur la météo et une variable cible correspondante, le jeu de jeux. Maintenant, nous devons classer les participants qui jouent et ceux qui ne jouent pas en fonction des conditions météorologiques.

  Étape 1: Convertissez le jeu de données en tableaux de fréquences.

  Étape 2: Créer une table de probabilité en utilisant une probabilité similaire, telle que 0.29 pour un Overcast et 0.64 pour un jeu.

  

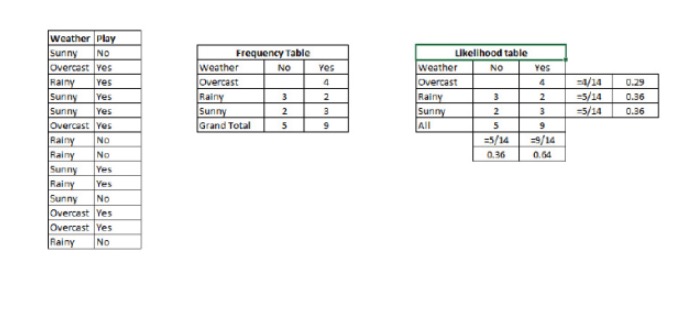
  Étape 3: Maintenant, utilisez les équations de Bayes simples pour calculer la probabilité postérieure de chaque catégorie. La catégorie avec la plus grande probabilité postérieure est le résultat de la prédiction.

  Question: Si le temps est beau, les participants peuvent jouer; est-ce vrai?

  Nous pouvons résoudre ce problème en utilisant la méthode décrite ci-dessus. Donc P (s'amuser) = P (s'amuser) * P (s'amuser) / P (s'amuser)

  Nous avons P = 3/9 = 0,33, P = 5/14 = 0,36, P = 9/14 = 0,64.

  Maintenant, p (je vais jouer) est égal à 0,33 fois 0,64 / 0,36 est égal à 0,60, avec une plus grande probabilité.

  Un procédé similaire est utilisé par Bayes pour prédire les probabilités de différentes catégories en utilisant différentes propriétés. Cet algorithme est souvent utilisé pour classer le texte, ainsi que pour des problèmes impliquant plusieurs catégories.

• Le code Python:

#Importer une bibliothèque depuis sklearn.naive_bayes import GaussianNB - Je ne sais pas. # Supposons que vous avez, X (préditeur) et Y (cible) pour l'ensemble de données de formation et x_test ((préditeur) de test_dataset

Créer un modèle d'objet de classification SVM = GaussianNB()

Il y a une autre distribution pour les classes multinomiales comme Bernoulli Naïf Bayes, lien de référence

Entraînez le modèle en utilisant les ensembles d'entraînement et vérifiez le score

model.fit(X, y) Je suis désolée. #Prédire les résultats prévue= modèle.prédit ((x_test)