1. Brève introduction

Les réseaux neuronaux profonds sont devenus de plus en plus populaires ces dernières années, résolvant des problèmes auparavant insolubles dans de nombreux domaines et démontrant leurs puissantes capacités. Dans la prédiction des séries chronologiques, le prix du réseau neuronal couramment utilisé est le RNN, car le RNN dispose non seulement de données d’entrée actuelles, mais également de données d’entrée historiques. Bien entendu, lorsque nous parlons de RNN prédisant les prix, nous parlons souvent d’un type de RNN :LSTM . Cet article construira un modèle pour prédire les prix du Bitcoin basé sur pytorch. Bien qu’il existe de nombreuses informations pertinentes sur Internet, elles ne sont toujours pas suffisamment complètes et relativement peu de personnes utilisent pytorch. Il est toujours nécessaire d’écrire un article. Le résultat final consiste à utiliser le prix d’ouverture, le prix de clôture et le prix le plus élevé , le prix le plus bas et le volume de transactions du marché Bitcoin. pour prédire le prochain cours de clôture. Mes connaissances personnelles sur les réseaux neuronaux sont moyennes et j’accepte vos critiques et corrections. Ce tutoriel est réalisé par FMZ, l’inventeur de la plateforme de trading quantitatif de devises numériques (www.fmz.com). Bienvenue dans le groupe QQ : 863946592 pour communiquer.

2. Données et références

Un exemple de prévision de prix connexe : https://yq.aliyun.com/articles/538484 Introduction détaillée au modèle RNN : https://zhuanlan.zhihu.com/p/27485750 Comprendre l’entrée et la sortie du RNN : https://www.zhihu.com/question/41949741/answer/318771336 À propos de pytorch : Documentation officielle https://pytorch.org/docs Recherchez vous-même d’autres informations. De plus, certaines connaissances préalables sont requises pour comprendre cet article, telles que les pandas/crawlers/traitement des données, etc., mais cela n’a pas d’importance si vous ne les connaissez pas.

3. Paramètres du modèle LSTM de Pytorch

Paramètres du LSTM :

Lorsque j’ai vu pour la première fois ces paramètres densément regroupés dans le document, ma réaction a été : En lisant lentement, j’ai finalement compris.

input_size: La taille de la caractéristique du vecteur d’entrée x. Si le cours de clôture est utilisé pour prédire le cours de clôture, alors input_size=1 ; si le cours de clôture est prédit par l’ouverture la plus haute et la clôture la plus basse, alors input_size=4 hidden_size: Taille de la couche cachée num_layers: Nombre de couches de RNN batch_first: Si True, la première dimension d’entrée est batch_size. Ce paramètre est également très déroutant et sera décrit en détail ci-dessous.

Paramètres des données d’entrée :

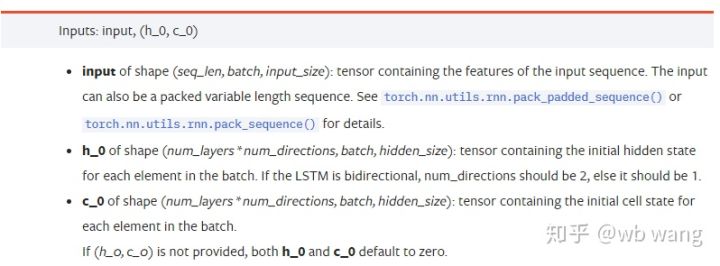
input:Les données d’entrée spécifiques sont un tenseur tridimensionnel avec une forme spécifique de (seq_len, batch, input_size). Parmi eux, seq_len fait référence à la longueur de la séquence, c’est-à-dire à la durée pendant laquelle les données historiques LSTM doivent être prises en compte. Notez que cela ne fait référence qu’au format des données, et non à la structure interne du LSTM. Le même modèle LSTM peut données d’entrée avec des seq_len différents et peuvent donner des prédictions. Résultat ; batch fait référence à la taille du lot, qui représente le nombre de groupes de données différents ; input_size est l’input_size précédent. h_0: État caché initial, la forme est (num_layers * num_directions, batch, hidden_size), s’il s’agit d’un réseau bidirectionnel num_directions=2 c_0:État initial de la cellule, la forme est la même que ci-dessus, peut être laissée non spécifiée.

Paramètres de sortie :

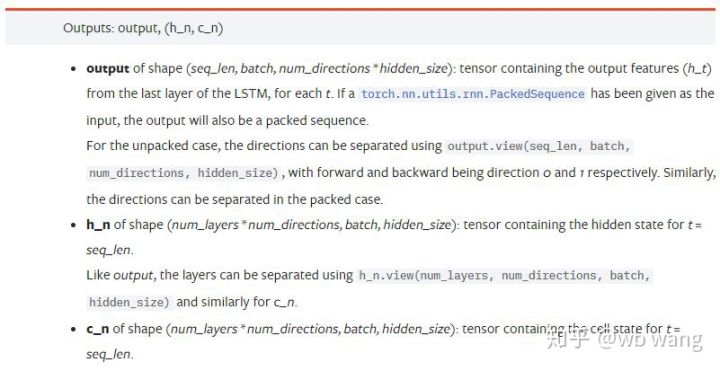
output: Forme de sortie (seq_len, batch, num_directions * hidden_size), notez qu’elle est liée au paramètre de modèle batch_first h_n: état h à l’instant t = seq_len, même forme que h_0 c_n: état c à l’instant t = seq_len, même forme que c_0

4. Exemple simple d’entrée et de sortie LSTM

Importez d’abord les packages requis

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

Définition du modèle LSTM

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

Préparation des données d’entrée

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

La forme de x est (3,4,5), puisque nous avons définibatch_first=True, à ce moment, batch_size est 3, sqe_len est 4 et input_size est 5. x[[0] représente le premier lot.

Si batch_first n’est pas défini, la valeur par défaut est False et les données sont représentées complètement différemment, avec une taille de lot de 4, sqe_len de 3 et input_size de 5. À ce moment-là x[0] représente les données de tous les lots à t=0, et ainsi de suite. Personnellement, je pense que ce paramètre n’est pas intuitif, j’ai donc ajouté le paramètrebatch_first=True.

La conversion des données entre les deux est également très pratique :x.permute(1,0,2)

Entrée et sortie

La forme de l’entrée et de la sortie LSTM est facile à confondre, avec l’aide de la figure suivante pour aider à comprendre :
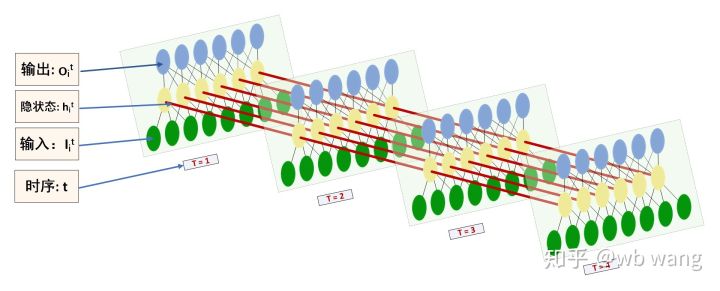
Source : https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

Observez les résultats de sortie, qui sont cohérents avec l’explication des paramètres précédents. Notez que la deuxième valeur de hn.size() est 3, ce qui est cohérent avec la taille de batch_size, indiquant qu’aucun état intermédiaire n’est enregistré dans hn, seulement la dernière étape. Étant donné que notre réseau LSTM comporte deux couches, la sortie de la dernière couche de hn est en fait la valeur de la sortie, et la forme de la sortie est[3, 4, 10], enregistre les résultats de tous les moments t=0,1,2,3, donc :

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. Préparez les données du marché Bitcoin

La plupart de ce que j’ai dit auparavant n’est qu’un prélude. Il est très important de comprendre l’entrée et la sortie de LSTM. Sinon, il est facile de faire des erreurs si vous copiez au hasard des codes à partir d’Internet. En raison de la puissante capacité de LSTM dans les séries chronologiques, même si le modèle est erroné, on peut l’obtenir à la fin. De bons résultats.

Acquisition de données

Les données utilisées sont les données de marché de la paire de trading BTC_USD de la bourse Bitfinex.

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

Le format des données est le suivant :

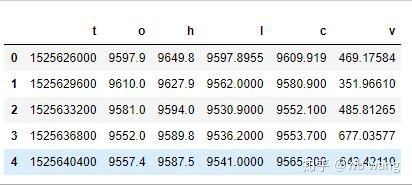
Prétraitement des données

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

La méthode de normalisation des données est très approximative et il y aura quelques problèmes. C’est juste à titre de démonstration. Vous pouvez utiliser une normalisation des données telle que Yield.

Préparation des données de formation

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

Les formes finales de train_x et train_y sont : torch.Size([800, 10, 5]), torch.Size([800, 10, 1]). Étant donné que notre modèle prédit le cours de clôture de la période suivante sur la base des données de 10 périodes, théoriquement, 800 lots ne nécessitent que 800 cours de clôture prédits. Mais train_y contient 10 données dans chaque lot. En fait, les résultats intermédiaires de chaque prédiction de lot sont conservés, pas seulement le dernier. Lors du calcul de la perte finale, les 10 résultats de prédiction peuvent être pris en compte et comparés aux valeurs réelles dans train_y. Théoriquement, il est également possible de calculer uniquement la perte du dernier résultat de prédiction. J’ai dessiné un schéma approximatif pour illustrer ce problème. Étant donné que le modèle LSTM ne contient pas réellement le paramètre seq_len, le modèle peut être appliqué à différentes longueurs et les résultats de prédiction intermédiaires sont également significatifs, j’ai donc tendance à fusionner le calcul de la perte.

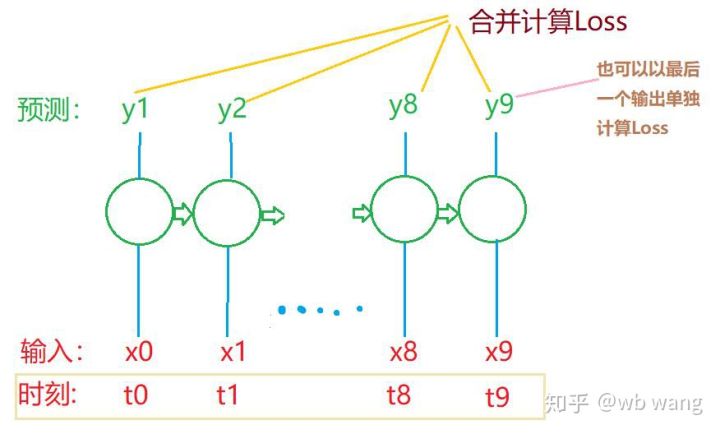
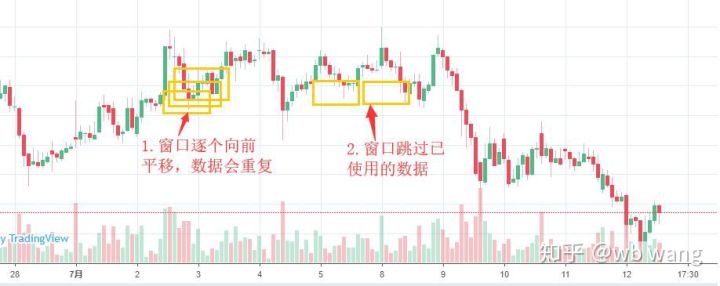
Notez que lors de la préparation des données d’entraînement, le mouvement de la fenêtre est saccadé et les données qui ont été utilisées ne le sont plus. Bien entendu, les fenêtres peuvent également être déplacées une par une, de sorte que l’ensemble d’entraînement obtenu sera beaucoup plus grand . Mais j’ai senti que les données de lots adjacentes étaient trop répétitives, j’ai donc adopté la méthode actuelle.

6. Construction du modèle LSTM

Le modèle final est le suivant, qui comprend un LSTM à deux couches et une couche linéaire.

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. Commencez à entraîner le modèle

J’ai enfin commencé l’entraînement, le code est le suivant :

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
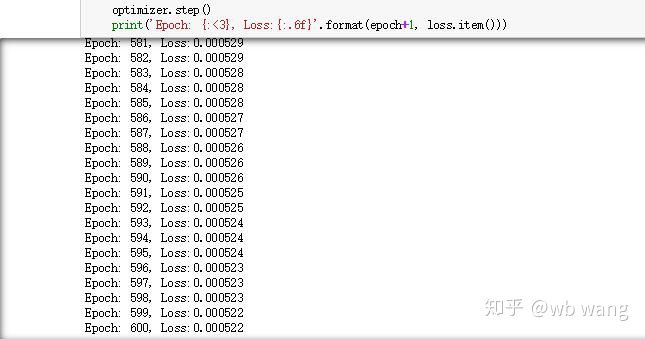
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

Les résultats de la formation sont les suivants :

8. Évaluation du modèle

Les valeurs prédites par le modèle sont :

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

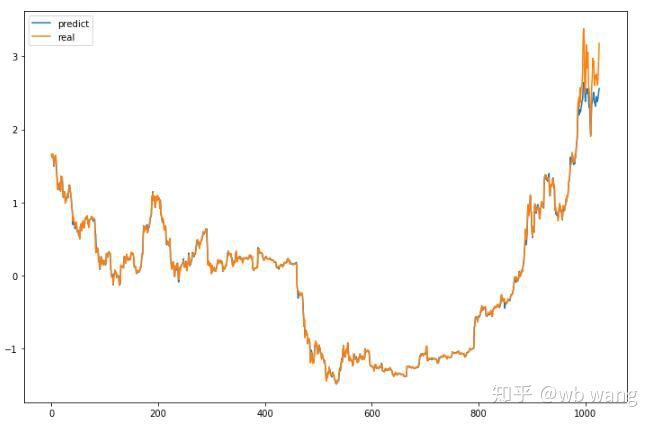
Comme on peut le voir sur la figure, le degré d’ajustement des données d’entraînement (avant 800) est très élevé, mais le prix du Bitcoin a atteint un nouveau sommet plus tard, et le modèle n’a pas vu ces données, donc la prédiction est incapable de bien performer. Cela montre également qu’il y avait un problème dans la standardisation précédente des données. Même si le prix prévu peut ne pas être exact, dans quelle mesure la prévision de la hausse et de la baisse est-elle exacte ? Jetez un œil à une section des données de prévision :

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

La précision de la prévision des hausses et des baisses a atteint 81,4 %, ce qui a dépassé mes attentes. Je ne sais pas si j’ai fait une erreur quelque part.

Bien sûr, ce modèle n’a aucune valeur réelle, mais il est simple et facile à comprendre. Utilisez-le simplement comme point de départ. D’autres cours d’introduction sur l’application des réseaux neuronaux à la quantification de la monnaie numérique seront proposés.