Stratégie de l'oscillateur Delta-RSI
Auteur:ChaoZhang est là., Date: le 30 mai 2022 à 11h01Les étiquettes:Indice de résistance
Stratégie de l'oscillateur Delta-RSI:
Cette stratégie illustre l'utilisation de l'oscillateur Delta-RSI récemment publié comme indicateur autonome.
Le delta-RSI représente une dérivée temporelle lissée du RSI, représentée sous forme d' histogramme et servant d' indicateur de dynamique.
Il existe trois conditions facultatives pour générer des signaux de négociation (définies séparément pour les signaux d'achat, de vente et de sortie): C'est-à-dire qu'il s'agit d'un indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur de la valeur de l'indicateur. L'indicateur D-RSI est un indicateur de tendance à la hausse lorsque le D-RSI traverse la ligne de signalisation de bas en haut de la ligne de signalisation (à défaut, baisse). Changement de direction: haussier lorsque le D-RSI est négatif et commence à monter (baissier autrement) Comme l'oscillateur D-RSI est basé sur l'ajustement polynomial de la courbe RSI, il est également possible de filtrer le signal commercial au moyen de l'erreur carrée moyenne de l'ajustement (normalisée par la moyenne d'échantillon).
test de retour
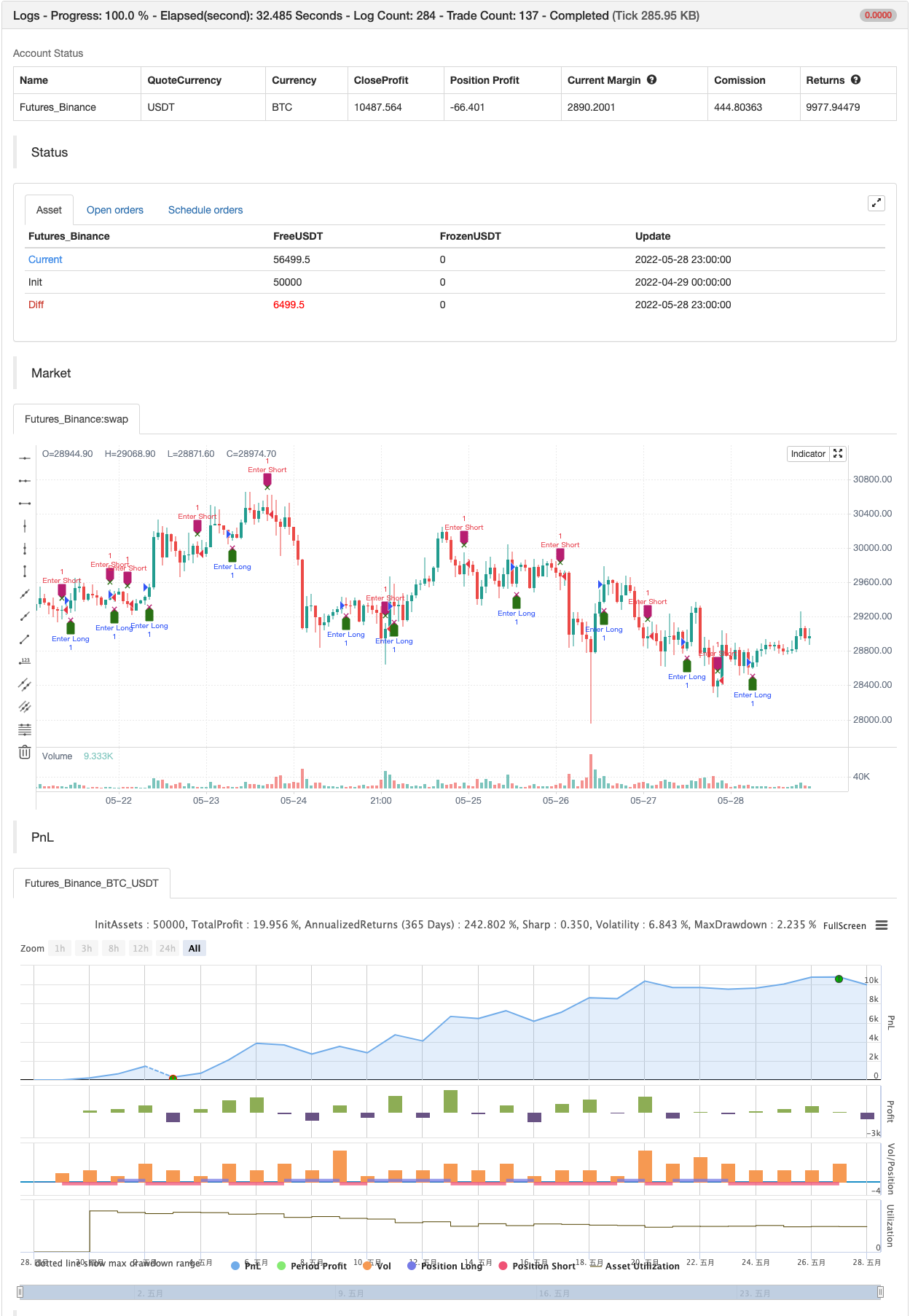
/*backtest
start: 2022-04-29 00:00:00
end: 2022-05-28 23:59:00
period: 1h
basePeriod: 15m
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © tbiktag
//
// Delta-RSI Oscillator Strategy
//
// A strategy that uses Delta-RSI Oscillator (© tbiktag) as a stand-alone indicator:
// https://www.tradingview.com/script/OXQVFTQD-Delta-RSI-Oscillator/
//
// Delta-RSI is a smoothed time derivative of the RSI, plotted as a histogram
// and serving as a momentum indicator.
//
// Input parameters:
// RSI Length: The timeframe of the RSI that serves as an input to D-RSI.
// Length: The length of the lookback frame used for local regression.
// Polynomial Order: The order of the local polynomial function used to interpolate the RSI.
// Signal Length: The length of a EMA of the D-RSI series that is used as a signal line.
// Trade signals are generated based on three optional conditions:
// - Zero-crossing: bullish when D-RSI crosses zero from negative to positive values (bearish otherwise)
// - Signal Line Crossing: bullish when D-RSI crosses from below to above the signal line (bearish otherwise)
// - Direction Change: bullish when D-RSI was negative and starts ascending (bearish otherwise)
//
// Since D-RSI oscillator is based on polynomial fitting of the RSI curve, there is also an option
// to filter trade signal by means of the root mean-square error of the fit (normalized by the sample average).
//
//@version=4
study(title="Delta-RSI Oscillator Strategy", shorttitle = "D-RSI", overlay = true)
// ---Subroutines---
matrix_get(_A,_i,_j,_nrows) =>
// Get the value of the element of an implied 2d matrix
//input:
// _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _i :: integer: row number
// _j :: integer: column number
// _nrows :: integer: number of rows in the implied 2d matrix
array.get(_A,_i+_nrows*_j)
matrix_set(_A,_value,_i,_j,_nrows) =>
// Set a value to the element of an implied 2d matrix
//input:
// _A :: array, changed on output: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _value :: float: the new value to be set
// _i :: integer: row number
// _j :: integer: column number
// _nrows :: integer: number of rows in the implied 2d matrix
array.set(_A,_i+_nrows*_j,_value)
transpose(_A,_nrows,_ncolumns) =>
// Transpose an implied 2d matrix
// input:
// _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _nrows :: integer: number of rows in _A
// _ncolumns :: integer: number of columns in _A
// output:
// _AT :: array: pseudo 2d matrix with implied dimensions: _ncolums x _nrows
var _AT = array.new_float(_nrows*_ncolumns,0)
for i = 0 to _nrows-1
for j = 0 to _ncolumns-1
matrix_set(_AT, matrix_get(_A,i,j,_nrows),j,i,_ncolumns)
_AT
multiply(_A,_B,_nrowsA,_ncolumnsA,_ncolumnsB) =>
// Calculate scalar product of two matrices
// input:
// _A :: array: pseudo 2d matrix
// _B :: array: pseudo 2d matrix
// _nrowsA :: integer: number of rows in _A
// _ncolumnsA :: integer: number of columns in _A
// _ncolumnsB :: integer: number of columns in _B
// output:
// _C:: array: pseudo 2d matrix with implied dimensions _nrowsA x _ncolumnsB
var _C = array.new_float(_nrowsA*_ncolumnsB,0)
int _nrowsB = _ncolumnsA
float elementC= 0.0
for i = 0 to _nrowsA-1
for j = 0 to _ncolumnsB-1
elementC := 0
for k = 0 to _ncolumnsA-1
elementC := elementC + matrix_get(_A,i,k,_nrowsA)*matrix_get(_B,k,j,_nrowsB)
matrix_set(_C,elementC,i,j,_nrowsA)
_C
vnorm(_X,_n) =>
//Square norm of vector _X with size _n
float _norm = 0.0
for i = 0 to _n-1
_norm := _norm + pow(array.get(_X,i),2)
sqrt(_norm)
qr_diag(_A,_nrows,_ncolumns) =>
//QR Decomposition with Modified Gram-Schmidt Algorithm (Column-Oriented)
// input:
// _A :: array: pseudo 2d matrix _A = [[column_0],[column_1],...,[column_(n-1)]]
// _nrows :: integer: number of rows in _A
// _ncolumns :: integer: number of columns in _A
// output:
// _Q: unitary matrix, implied dimenstions _nrows x _ncolumns
// _R: upper triangular matrix, implied dimansions _ncolumns x _ncolumns
var _Q = array.new_float(_nrows*_ncolumns,0)
var _R = array.new_float(_ncolumns*_ncolumns,0)
var _a = array.new_float(_nrows,0)
var _q = array.new_float(_nrows,0)
float _r = 0.0
float _aux = 0.0
//get first column of _A and its norm:
for i = 0 to _nrows-1
array.set(_a,i,matrix_get(_A,i,0,_nrows))
_r := vnorm(_a,_nrows)
//assign first diagonal element of R and first column of Q
matrix_set(_R,_r,0,0,_ncolumns)
for i = 0 to _nrows-1
matrix_set(_Q,array.get(_a,i)/_r,i,0,_nrows)
if _ncolumns != 1
//repeat for the rest of the columns
for k = 1 to _ncolumns-1
for i = 0 to _nrows-1
array.set(_a,i,matrix_get(_A,i,k,_nrows))
for j = 0 to k-1
//get R_jk as scalar product of Q_j column and A_k column:
_r := 0
for i = 0 to _nrows-1
_r := _r + matrix_get(_Q,i,j,_nrows)*array.get(_a,i)
matrix_set(_R,_r,j,k,_ncolumns)
//update vector _a
for i = 0 to _nrows-1
_aux := array.get(_a,i) - _r*matrix_get(_Q,i,j,_nrows)
array.set(_a,i,_aux)
//get diagonal R_kk and Q_k column
_r := vnorm(_a,_nrows)
matrix_set(_R,_r,k,k,_ncolumns)
for i = 0 to _nrows-1
matrix_set(_Q,array.get(_a,i)/_r,i,k,_nrows)
[_Q,_R]
pinv(_A,_nrows,_ncolumns) =>
//Pseudoinverse of matrix _A calculated using QR decomposition
// Input:
// _A:: array: implied as a (_nrows x _ncolumns) matrix _A = [[column_0],[column_1],...,[column_(_ncolumns-1)]]
// Output:
// _Ainv:: array implied as a (_ncolumns x _nrows) matrix _A = [[row_0],[row_1],...,[row_(_nrows-1)]]
// ----
// First find the QR factorization of A: A = QR,
// where R is upper triangular matrix.
// Then _Ainv = R^-1*Q^T.
// ----
[_Q,_R] = qr_diag(_A,_nrows,_ncolumns)
_QT = transpose(_Q,_nrows,_ncolumns)
// Calculate Rinv:
var _Rinv = array.new_float(_ncolumns*_ncolumns,0)
float _r = 0.0
matrix_set(_Rinv,1/matrix_get(_R,0,0,_ncolumns),0,0,_ncolumns)
if _ncolumns != 1
for j = 1 to _ncolumns-1
for i = 0 to j-1
_r := 0.0
for k = i to j-1
_r := _r + matrix_get(_Rinv,i,k,_ncolumns)*matrix_get(_R,k,j,_ncolumns)
matrix_set(_Rinv,_r,i,j,_ncolumns)
for k = 0 to j-1
matrix_set(_Rinv,-matrix_get(_Rinv,k,j,_ncolumns)/matrix_get(_R,j,j,_ncolumns),k,j,_ncolumns)
matrix_set(_Rinv,1/matrix_get(_R,j,j,_ncolumns),j,j,_ncolumns)
//
_Ainv = multiply(_Rinv,_QT,_ncolumns,_ncolumns,_nrows)
_Ainv
norm_rmse(_x, _xhat) =>
// Root Mean Square Error normalized to the sample mean
// _x. :: array float, original data
// _xhat :: array float, model estimate
// output
// _nrmse:: float
float _nrmse = 0.0
if array.size(_x) != array.size(_xhat)
_nrmse := na
else
int _N = array.size(_x)
float _mse = 0.0
for i = 0 to _N-1
_mse := _mse + pow(array.get(_x,i) - array.get(_xhat,i),2)/_N
_xmean = array.sum(_x)/_N
_nrmse := sqrt(_mse) /_xmean
_nrmse
diff(_src,_window,_degree) =>
// Polynomial differentiator
// input:
// _src:: input series
// _window:: integer: wigth of the moving lookback window
// _degree:: integer: degree of fitting polynomial
// output:
// _diff :: series: time derivative
// _nrmse:: float: normalized root mean square error
//
// Vandermonde matrix with implied dimensions (window x degree+1)
// Linear form: J = [ [z]^0, [z]^1, ... [z]^degree], with z = [ (1-window)/2 to (window-1)/2 ]
var _J = array.new_float(_window*(_degree+1),0)
for i = 0 to _window-1
for j = 0 to _degree
matrix_set(_J,pow(i,j),i,j,_window)
// Vector of raw datapoints:
var _Y_raw = array.new_float(_window,na)
for j = 0 to _window-1
array.set(_Y_raw,j,_src[_window-1-j])
// Calculate polynomial coefficients which minimize the loss function
_C = pinv(_J,_window,_degree+1)
_a_coef = multiply(_C,_Y_raw,_degree+1,_window,1)
// For first derivative, approximate the last point (i.e. z=window-1) by
float _diff = 0.0
for i = 1 to _degree
_diff := _diff + i*array.get(_a_coef,i)*pow(_window-1,i-1)
// Calculates data estimate (needed for rmse)
_Y_hat = multiply(_J,_a_coef,_window,_degree+1,1)
float _nrmse = norm_rmse(_Y_raw,_Y_hat)
[_diff,_nrmse]
/// --- main ---
degree = input(title="Polynomial Order", group = "Model Parameters:",
inline = "linepar1", type = input.integer, defval=2, minval = 1)
rsi_l = input(title = "RSI Length", group = "Model Parameters:",
inline = "linepar1", type = input.integer, defval = 21, minval = 1,
tooltip="The period length of RSI that is used as input.")
window = input(title="Length ( > Order)", group = "Model Parameters:",
inline = "linepar2", type = input.integer, defval=21, minval = 2)
signalLength = input(title="Signal Length", group = "Model Parameters:",
inline = "linepar2", type=input.integer, defval=9,
tooltip="The signal line is a EMA of the D-RSI time series.")
islong = input(title = "Buy", group = "Show Signals:",
inline = "lineent",type = input.bool, defval = true)
isshort = input(title = "Sell", group = "Show Signals:",
inline = "lineent", type = input.bool, defval= true)
showendlabels = input(title = "Exit", group = "Show Signals:",
inline = "lineent", type = input.bool, defval= true)
buycond = input(title="Buy", group = "Entry and Exit Conditions:",
inline = "linecond",type = input.string, defval="Zero-Crossing",
options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
sellcond = input(title="Sell", group = "Entry and Exit Conditions:",
inline = "linecond",type = input.string, defval="Zero-Crossing",
options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
endcond = input(title="Exit", group = "Entry and Exit Conditions:",
inline = "linecond",type = input.string, defval="Zero-Crossing",
options=["Zero-Crossing", "Signal Line Crossing","Direction Change"])
usenrmse = input(title = "", group = "Filter by Means of Root-Mean-Square Error of RSI Fitting:",
inline = "linermse",type = input.bool, defval = false)
rmse_thrs = input(title = "RSI fitting Error Threshold, %", type = input.float,
group = "Filter by Means of Root-Mean-Square Error of RSI Fitting:",
inline = "linermse", defval = 10, minval = 0.0) /100
src = rsi(close,rsi_l)
[drsi,nrmse] = diff(src,window,degree)
signalline = ema(drsi, signalLength)
// Conditions and filters
filter_rmse = usenrmse?nrmse<rmse_thrs:true
dirchangeup = (drsi>drsi[1]) and (drsi[1]<drsi[2]) and drsi[1]<0.0
dirchangedw = (drsi<drsi[1]) and (drsi[1]>drsi[2]) and drsi[1]>0.0
crossup = crossover(drsi,0.0)
crossdw = crossunder(drsi,0.0)
crosssignalup = crossover(drsi,signalline)
crosssignaldw = crossunder(drsi,signalline)
//Signals
golong = (buycond=="Direction Change"?dirchangeup:(buycond=="Zero-Crossing"?crossup:crosssignalup)) and filter_rmse
goshort= (sellcond=="Direction Change"?dirchangedw:(sellcond=="Zero-Crossing"?crossdw:crosssignaldw)) and filter_rmse
endlong = (endcond=="Direction Change"?dirchangedw:(endcond=="Zero-Crossing"?crossdw:crosssignaldw)) and filter_rmse
endshort= (endcond=="Direction Change"?dirchangeup:(endcond=="Zero-Crossing"?crossup:crosssignalup)) and filter_rmse
plotshape((golong and islong) ? low : na, location=location.belowbar, style=shape.labelup, color=#2E7C13, size=size.small, title='Buy')
plotshape((goshort and isshort) ? high: na, location=location.abovebar, style=shape.labeldown, color=#BF217C, size=size.small, title='Sell')
plotshape((showendlabels and endlong and islong) ? high: na, location=location.abovebar, style=shape.xcross, color=#2E7C13, size=size.tiny, title='Exit Long')
plotshape((showendlabels and endshort and isshort) ? low : na, location=location.belowbar, style=shape.xcross, color=#BF217C, size=size.tiny, title='Exit Short')
alertcondition(golong, title='Long Signal', message='D-RSI: Long Signal')
alertcondition(goshort, title='Short Signal', message='D-RSI: Short Signal')
alertcondition(endlong, title='Exit Long Signal', message='D-RSI: Exit Long')
alertcondition(endshort, title='Exit Short Signal', message='D-RSI: Exit Short')
if golong
strategy.entry("Enter Long", strategy.long)
else if goshort
strategy.entry("Enter Short", strategy.short)
- Système stratégique de quantification des tendances de la mobilité à deux indicateurs
- Stratégie de négociation de tendance à signaux multiples à double équilibre RSI
- Stratégie d'optimisation des transactions journalières combinée à l'indicateur de dynamique RSI
- Stratégie de suivi des tendances de la dynamique à travers plusieurs indicateurs technologiques
- Stratégie de suivi de la tendance de la forme de la colonne d'éléphant pour une correction dynamique des pertes
- Stratégie de dynamique de tendance RSI bicyclique combinée à un système de gestion de position pyramidale
- Stratégie de négociation quantifiée par paramètres dynamiques RSI à travers plusieurs lignes uniformes
- Les tendances dynamiques déterminent la stratégie de croisement des indicateurs RSI
- Algorithmes de négociation de l'analyse quantitative des prix à proximité K multidimensionnelle et de la forme de la chute
- Système de commutation dynamique multi-stratégique adaptatif: stratégie de négociation quantitative pour suivre les tendances de convergence et les perturbations de la plage
- Des stratégies de quantification avancées croisent des tendances multidimensionnelles et de multiples indicateurs
- Indicateur de configuration de démarrage
- Indice de change stochastique extrême
- Indicateur MACD BB V 1,00
- SAR parabolique
- Indicateur de divergence RSI
- Indicateur OBV MACD
- Tendance de pivot
- Stratégie de divergence des prix v1.0
- Dépassement du support-résistance
- Moyenne mobile adaptative de pente
- Stratégie de cryptographie à faible balayage
- [blackcat] L2 stratégie de renversement des étiquettes
- SuperB
- SAR élevé SAR bas
- SuperTREX
- Détecteur de pic
- Détecteur bas
- Tendance de la SMA
- Bas de Bollinger
- Super tendance B