कुर्टोसिस और तिरछापन

• #### कर्टोसिस और स्केवनेस

पोस्ट किया गयाः EasyTrader

यह एक व्यापारिक रणनीति है जो कि एक वितरण के साथ एक व्यापारिक रणनीति है। जब डेटा ट्रेंडिंग होता है और संभावित प्रवृत्ति सकारात्मक होती है, तो हम अधिक करते हैं। जब डेटा ट्रेंडिंग होता है और संभावित प्रवृत्ति नकारात्मक होती है, तो हम शून्य करते हैं। जब प्रवृत्ति उलट जाती है, तो हम बराबरी करते हैं।

तो, हम प्रवृत्तियों और प्रवृत्तियों की ताकत कैसे निर्धारित कर सकते हैं? सबसे पहले, हम शिखर और विचलन की परिभाषाओं पर एक नज़र डालते हैं।

पहले हम सामान्य वितरण की परिभाषा को देखेंगे

वितरण (distribution): एक वितरण स्थिति जिसमें चर में सभी संख्याओं की आवृत्ति होती है, चर संख्याओं के लिए क्षैतिज अक्ष के रूप में और आवृत्ति के लिए ऊर्ध्वाधर अक्ष के रूप में प्रदर्शित होती है। सामान्य वितरणः जिसे गौसियन वितरण भी कहा जाता है

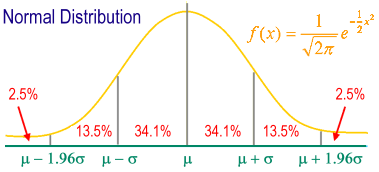
मानक सामान्य वितरण: औसत (mean) के साथ केंद्र, मानक विचलन (standard deviation) के रूप में सूचकांक अक्ष की मूलभूत इकाइयों में चित्रित सामान्य वितरण ग्राफ। घण्टी के आकार का सममित ग्राफ।

m ± 1s में 68.26% व्यक्ति शामिल हैं।

m ± 2s पूरे नमूना समूह के 95.44% व्यक्तियों को शामिल करता है।

m ± 3s पूरे नमूना समूह के 99.74% व्यक्तियों को शामिल करता है।

95% व्यक्ति m ± 1.96s के बीच आते हैं।

99% व्यक्ति m ± 2.58s के बीच आते हैं।

सांख्यिकी में, चोटी (Kurtosis) वास्तविक संख्या में यादृच्छिक चर की संभावनाओं के वितरण की चोटी को मापता है। उच्च चोटी का अर्थ है कि विचलन में वृद्धि कम आवृत्ति के लिए औसत से अधिक या कम चरम विचलन के कारण होती है।

चोटी (अंग्रेज़ीः peak, kurtosis) एक आंकड़ा है जो डेटा के एक समूह के वितरण के पैटर्न को दर्शाता है। सामान्य वितरण की चोटी 3 है, इसलिए हम 3 से अधिक की चोटी को चोटी कहते हैं, यह दर्शाता है कि वितरण सामान्य वितरण की तुलना में अधिक केंद्रित और सामंजस्यपूर्ण है। हम 3 से कम की चोटी को समतल चोटी कहते हैं, यह दर्शाता है कि वितरण सकारात्मक वितरण की तुलना में अधिक चिकनी है। यहां हम वास्तविक चोटी को घटाकर 3 के बाद के मूल्य को संदर्भित करते हैं। वित्तीय बाजारों में, 0 से अधिक की चोटी को ट्रेंडिंग बाजार के रूप में दर्शाया जाता है, जबकि 0 से कम की चोटी ट्रेंडिंग बाजार के रूप में दर्शाई जाती है।

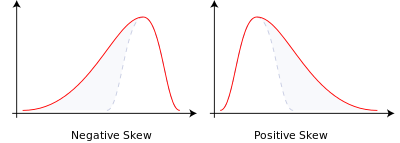
skewness (अंग्रेज़ीः skewness) डेटा के वितरण की समरूपता को दर्शाता है, या डेटा में बहुवचनों के मोड की स्थिति को दर्शाता है। एक पूर्ण समरूपता को दर्शाता है जो कि 0 के बराबर है। यह आँकड़ा सामान्य वितरण की तुलना के लिए भी आवश्यक है। सामान्य वितरण की तुलना में 0 से अधिक का विचलन दिखाता है कि सरणी दाईं ओर झुकी हुई है, जो दाईं ओर की लंबी पूंछ के रूप में प्रदर्शित होती है और चरम मूल्य दाईं ओर से अधिक प्रदर्शित होती है; इसके विपरीत, बाएं, जो बाईं ओर की लंबी पूंछ के रूप में प्रदर्शित होती है और चरम मूल्य बाईं ओर से अधिक प्रदर्शित होती है। वित्तीय बाजारों में, 0 से अधिक का विचलन डेटा को शब्दकोश की ओर झुकाव के रूप में समझा जा सकता है, 0 से कम का विचलन डेटा को शब्दकोश के नीचे झुकाव के रूप में समझा जा सकता है।

संभाव्यता सिद्धांत और सांख्यिकी में, विचलन वास्तविक संख्यात्मक यादृच्छिक चरों के संभाव्यता वितरण की असमानता को मापता है। विचलन के मान सकारात्मक हो सकते हैं, नकारात्मक हो सकते हैं या यहां तक कि परिभाषित नहीं किए जा सकते हैं। संख्यात्मक रूप से, विचलन नकारात्मक है (नकारात्मक विचलन) का अर्थ है कि संभावना घनत्व फ़ंक्शन के बाईं ओर की पूंछ दाईं ओर की तुलना में अधिक लंबी है, जिसमें अधिकांश मूल्य (मध्यम सहित) औसत के दाईं ओर स्थित हैं।

यह दो प्रकार के होते हैं:

• नकारात्मक या बाएं पक्षीय: बाएं पक्ष का पूंछ लंबा है, और वितरण का मुख्य भाग दाईं ओर केंद्रित है।
• ध्रुवीय या दाहिनी ओर: दाहिनी ओर का पूंछ लंबा होता है, और वितरण का मुख्य भाग बाईं ओर केंद्रित होता है।
• यदि वितरण सममित है, तो औसत = मध्य, और विचलन शून्य है (इसके अलावा, यदि वितरण एकल-शिखर वितरण है, तो औसत = मध्य = बहु) ।

• इस प्रकार, हम निम्नलिखित लेन-देन के नियमों को प्राप्त करते हैंः जब चोटी 0 से कम है (बाजार में एक प्रवृत्ति है), विचलन N से अधिक है (प्रवृत्ति ऊपर की ओर है), अधिक करें; जब पीक 0 से कम होता है (बाजार ट्रेंडिंग बाजार में है), विचलन M से कम होता है (ट्रेंडिंग नीचे है), और शून्य होता है;

MATLAB: जो लोग रुचि रखते हैं वे इसे जेएस भाषा में बदल सकते हैं।

input:ExitType(5) ;
input:NBarL(2),NBarS(2),TradeProfit(0.053),TradeStopLoss(0.023),ATRs_L(5.4),ATRs_S(10.9);
vars: IsBalanceDay(False),MP(0),PF(0),PL(0),HLRange(100);

inputs:Length(20),Trigger(3),UpSkew(3.4),DownSkew(2.2) ;
vars:KurtValue(0),SkewValue(0),BuyPoint(0),SellPoint(0);

MP = MarketPosition ;
if DAYofMonth(Date) > 14 and DAYofMonth(Date) < 22 and DAYofWeek(Date)= 3 then isBalanceDay = True else isBalanceDay =False ;

PF = AvgPrice*TradeProfit ;
PL = AvgPrice*TradeStopLoss ;

{计算峰度 }
KurtValue = Kurtosis(Close,Length) ;
{计算偏度}
SkewValue = Skew(Close,Length) ;

{ 峰度向下跌破 Trigger 线 ,建立买卖点 }
if KurtValue Cross under Trigger then Begin
BuyPoint = High 3;
SellPoint = Low-3;
end;

{ 偏度大于某数值后 ,趋势确认进场作多 }
if  SkewValue > -UpSkew 2 then Buy next bar at BuyPoint stop ;
{ 偏度小于某数值后 ,趋势确认进场作空 }
if  SkewValue < -DownSkew 2 then Sell next bar at SellPoint Stop ;
end;

if ExitType = 1 then SetStopLoss(PL * BigPointValue) ;

if ExitType = 2 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
end;

if ExitType = 3 then Begin
if MP > 0 and BarsSinceEntry = NBarL then ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then ExitShort next bar at Market ;
end;

if ExitType = 4 then Begin
SetStopLoss(PL * BigPointValue) ;
setProfitTarget(PF * BigPointValue) ;
if MP > 0 and BarsSinceEntry = NBarL then {Sell } ExitLong next bar at Market ;
if MP < 0 and BarsSinceEntry = NBarS then {Buy} ExitShort next bar at Market ;
end;

if ExitType = 5 then Begin
{*******************************************************************
Description : ATR Trailing Stop Long Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
********************************************************************}
{Inputs: ATRs_L(3);}
Variables: PosHigh(0), ATRVal_L(0);

ATRVal_L = AvgTrueRange(10) * ATRs_L;
If BarsSinceEntry = 0 Then PosHigh = High;
If MarketPosition = 1 Then Begin
If High > PosHigh Then PosHigh = High;
ExitLong ("ATR") Next Bar at PosHigh - ATRVal_L Stop;
End else ExitLong ("ATR eb") Next bar at High - ATRVal_L Stop;

{*******************************************************************
Description : ATR Trailing Stop Short Exit
Provided By : Omega Research, Inc. (c) Copyright 1999
******************************************************************}
{Inputs: ATRs_S(3);}
Variables: PosLow(0), ATRVal_S(0);

ATRVal_S = AvgTrueRange(10) * ATRs_S;
If BarsSinceEntry = 0 Then PosLow = Low;
If MarketPosition = -1 Then Begin
If Low < PosLow Then PosLow = Low;
ExitShort ("ATR_1") Next Bar at PosLow ATRVal_S Stop;
End else ExitShort ("ATR_1 eb") Next bar at Low ATRVal_S Stop;
end;

if IsBalanceDay then setExitonClose ;

Faruto के ब्लॉग से पुनर्प्रकाशित