Klasifikasi Bayesian berdasarkan algoritma KNN

Dasar teoretis untuk merancang klasifikasi untuk membuat keputusan klasifikasi Teori Keputusan Bayesian:

Perbandingan P(ωi 11:1x) ⋅ di mana ωi adalah kelas i, x adalah data yang diamati dan harus diklasifikasikan, P(ωi 11:1x) menunjukkan seberapa besar probabilitas untuk menilai bahwa data tersebut termasuk dalam kelas i dalam keadaan ada vektor karakteristik yang diketahui, yang juga menjadi probabilitas penyesuaian. Berdasarkan rumus Bayes, dapat dinyatakan sebagai:

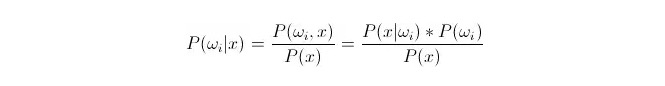
Di antaranya, P (x) disebut probabilitas mirip atau probabilitas berkondisi; P (ω) disebut probabilitas terdahulu, karena tidak terkait dengan percobaan dan dapat diketahui sebelum percobaan.

Dalam pengklasifikasian, diberikan x, pilihlah kategori yang membuat probabilitas retrospektif P ((ωiⴰⵙⴰⵙx) terbesar. Dalam perbandingan setiap kategori P ((ωiⴰⵙx) kecil,ωi adalah variabel, dan x adalah tetap; sehingga P ((x) dapat dihilangkan, tidak diperhitungkan.

Jadi hasilnya adalah P (x) = P (x) = P (x) =*Pertanyaan P ((ωi) }} Probabilitas awal P ((ωi) adalah proporsi dari data yang muncul di bawah setiap klasifikasi yang terfokus pada pelatihan statistik.

Kemungkinan P (x < i < i) adalah perhitungan yang rumit, karena x adalah data dari test set, dan tidak dapat diperoleh secara langsung dari set latihan. Maka kita perlu mencari hukum distribusi dari data set latihan, dan kemudian kita akan mendapatkan P (x < i < i) < i < i.

Berikut adalah k algoritma berdekatan, dalam bahasa Inggris disebut KNN.

Kita akan menyesuaikan distribusi dari data yang ada di dalam training set x1, x2…xn (di mana setiap data adalah dimensi m), di bawah kategoriωi. Dengan x sebagai titik manapun dalam ruang dimensi m, bagaimana menghitung P ((x danωi)?

Kita tahu bahwa ketika jumlah data cukup besar, kita dapat menggunakan perkiraan probabilitas secara proporsional. Gunakan prinsip ini untuk mencari k titik sampel yang paling dekat dengan titik x, di antaranya termasuk kategori i.

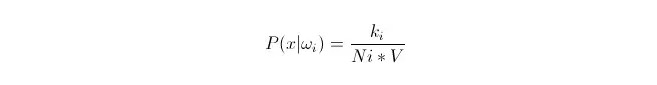
Jadi kita bisa melihat bahwa kita telah menghitung densitas probabilitas kelas pada titik x.

Bagaimana dengan P (ωi)? Berdasarkan metode di atas, P ((ωi) = Ni/N 。 di mana N adalah jumlah sampel。 Jadi, kita bisa mengatakan bahwa P (x) = k/N.*V), di mana k adalah jumlah dari semua titik sampel yang mengelilingi superbola ini; N adalah jumlah sampel. Jadi P (ωi regex) dapat dihitung: dengan rumus ini, mudah untuk mendapatkan:

P(ωi|x)=ki/k

Untuk menjelaskan persamaan di atas, dalam sebuah superbola berukuran V, kita mengelilingi k sampel, di antaranya ada ki dari kelas i. Dengan demikian, sampel apa yang paling banyak dikelilingi, kita dapat menentukan mana dari x yang seharusnya termasuk dalam kelas tersebut. Ini adalah pengelompokan yang dirancang dengan k algoritma berdekatan.