Aplikasi Python Bayes yang sederhana

Dengan asumsi bahwa variabel-variabel yang diprediksi saling independen, dapat diperoleh metode klasifikasi Bayesian sederhana berdasarkan teorema Bayesian. Dengan kata lain, klasifikasi Bayesian sederhana mengasumsikan bahwa suatu sifat dari suatu klasifikasi tidak terkait dengan sifat-sifat lain dari klasifikasi tersebut. Misalnya, jika sebuah buah bulat dan merah, dan berdiameter sekitar 3 inci, maka buah tersebut mungkin adalah apel. Bahkan jika sifat-sifat tersebut saling bergantung, atau tergantung pada adanya sifat-sifat lain, klasifikasi Bayesian sederhana akan mengasumsikan bahwa sifat-sifat tersebut secara terpisah mengisyaratkan bahwa buah tersebut adalah apel.

• Model Bayesian sederhana mudah dibangun, dan sangat berguna untuk data set besar. Meskipun sederhana, namun Bayesian sederhana dapat ditampilkan di luar metode klasifikasi yang sangat rumit.

  Bayes' theorem memberikan sebuah metode untuk menghitung probabilitas posteriori P (c) x dari P©, P (x) dan P (x) c. Lihat persamaan berikut:

  

  Di sini,

  P (c) adalah probabilitas posteriori dari suatu kelas (target) dengan asumsi bahwa variabel (properti) yang diprediksi diketahui P© adalah probabilitas terdahulu dari kelas P (x) adalah probabilitas, yaitu kemungkinan variabel yang diprediksikan dalam kondisi kelas yang diketahui. P (x) adalah probabilitas awal dari variabel yang diprediksi Contoh: Mari kita gunakan contoh untuk memahami konsep ini. Di bawah ini, saya memiliki set latihan cuaca dan variabel target yang sesuai dengan Play Play. Sekarang, kita perlu mengklasifikasikan peserta yang akan bermain dan tidak bermain berdasarkan kondisi cuaca. Mari kita lakukan langkah-langkah berikut.

  Langkah 1: Mengkonversi dataset ke tabel frekuensi.

  Langkah 2: Membuat tabel likelihood dengan menggunakan probabilitas seperti Overcast 0.29 dan probabilitas bermain 0.64.

  

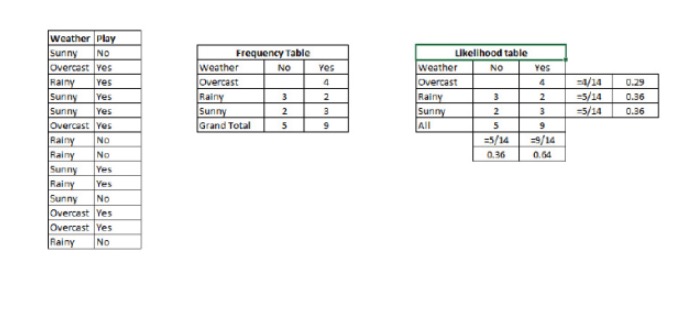
  Langkah 3: Sekarang, gunakan persamaan Bayesian sederhana untuk menghitung probabilitas posteriori dari setiap kelas. Kelas dengan probabilitas posteriori terbesar adalah hasil dari prediksi.

  Pertanyaan: Jika cuaca cerah, peserta bisa bermain.

  Kita bisa menyelesaikan masalah ini dengan menggunakan metode yang telah kita bahas sebelumnya. Jadi, P (bermain) = P (bermain)

  Jadi kita memiliki P (bermain) = 3/9 = 0.33, P (bermain) = 5/14 = 0.36, P (bermain) = 9/14 = 0.64.

  Sekarang, P (akan bermain) = 0.33 kali 0.64 / 0.36 = 0.60, ada kemungkinan yang lebih besar.

  Bayes yang polos menggunakan metode yang mirip untuk memprediksi kemungkinan dari berbagai kategori melalui sifat yang berbeda. Algoritma ini biasanya digunakan untuk klasifikasi teks, serta masalah yang melibatkan beberapa kategori.

• Kode Python:

#Impor Perpustakaan dari sklearn.naive_bayes import GaussianNB Aku tidak tahu. # Diasumsikan Anda memiliki, X (prediktor) dan Y (target) untuk pelatihan data set dan x_test(prediktor) dari test_dataset

Buat model objek klasifikasi SVM = GaussianNB()

ada distribusi lain untuk kelas multinomial seperti Bernoulli Naif Bayes, Refer link

Latih model menggunakan set pelatihan dan periksa skor

model.fit(X, y) Aku tidak tahu. #Prediksi Output diprediksi= model.predict ((x_test)