Python 朴素なベイズアプリケーション

予測変数間の相互独立を前提として,バイエスの定理に基づいて,素朴なバイエスの分類方法が得られる.より単純に言えば,素朴なバイエスの分類器は,ある分類の特性が他の分類の特性に関係がないと仮定する.例えば,もし果物が丸い赤色で,直径約3インチであれば,それはおそらくリンゴである.これらの特性が相互依存している場合でも,または他の特性の存在に依存している場合でも,素朴なバイエスの分類器は,これらの特性がそれぞれ独立して,この果物がリンゴであることを暗示することを仮定する.

• シンプルなベイエスモデルは簡単に構築され,大規模なデータセットに非常に有用である.単純であるにもかかわらず,シンプルなベイエスの表現は非常に複雑な分類方法を超えています.

  Bayes定理は,P©,P (x) とP (x) について計算する後期実験確率P (c) の方法を提供する.以下の方程式を参照してください.

  

  市民の関心は

  P (c) は,既知の予測変数 (c) の条件 (c) で,クラス (c) の目標 (c) の後期確率である. P©は,そのクラスの先行確率です. P (x) は,既知のクラスで予測される変数の確率である. P (x) は前向きな確率です. 例:この概念を例で理解しましょう. 下には,私は天候のトレーニングセットと対応する目標変数 Play を持っています. 今,私たちは天候に応じて,会場でプレイする参加者とプレイしない参加者を分類する必要があります. 次の手順を実行しましょう.

  ステップ1:データセットを周波数表に変換します.

  ステップ2: Overcast の確率が 0.29 のとき,プレイの確率が 0.64 のとき,類似のを用いて,Likelihood 表を作成します.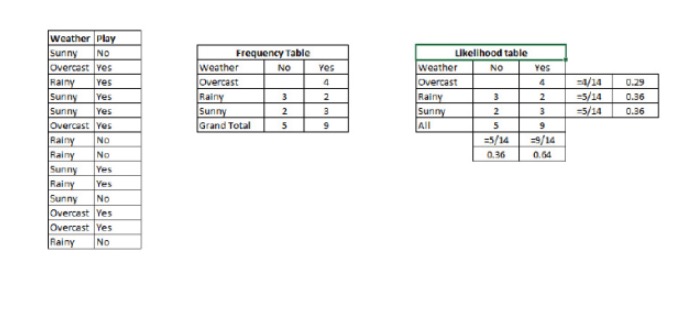

  

  ステップ3:現在,単純なベイエスの方程式を使用して,各クラスの後期確率を計算します.後期確率が最も高いクラスの結果は予測結果です.

  Q: 晴れた天気であれば,参加者は遊べる.

  この問題を解くには 先ほどお話しした方法を使います. つまり,P (遊び) =P (遊び) *P (遊び) /P (遊び)

  3/9=0.33です. 5/14=0.36です. 9/14=0.64です.

  確率より大きいです. 確率より大きいです. 確率より大きいです.

  素朴なベイエスは,異なる属性によって異なるカテゴリーの確率を予測する類似の方法を使用している.このアルゴリズムは,テキストの分類,および複数のカテゴリーを含む問題のために一般的に使用される.

• Python コード:

#図書館をインポートする sklearn.naive_bayesから GaussianNBをインポートする わかった 訓練データセットのX (予測者) とY (ターゲット) とtest_datasetのx_test (予測者) を持っているとします.

SVM分類オブジェクトモデルを作成 = GaussianNB()

バルヌーリ,ナイヴ・ベイズ,参照リンクなど,多項式クラスには別の分布があります.

訓練セットを使用してモデルを訓練し,スコアをチェック

model.fit(X,y) わかった #出力を予測する 予測=モデル.予測 (x_テスト)