1. 簡単な紹介

近年、ディープニューラルネットワークの人気が高まり、多くの分野でこれまで解決できなかった問題を解決し、その強力な能力を実証しています。時系列の予測では、RNNが一般的に使用されるニューラルネットワークの価格です。RNNは現在のデータ入力だけでなく、履歴データ入力も持っているからです。もちろん、価格を予測するRNNについて話すとき、RNNのタイプについて話すことが多いです。 : LSTM 。この記事では、PyTorch に基づいてビットコインの価格を予測するモデルを構築します。インターネット上には関連情報がたくさんあるが、まだ十分に徹底されておらず、pytorchを使用する人は比較的少ない。それでも記事を書く必要がある。最終的な結果は、始値、終値、最高値を使用することです。ビットコイン市場の価格、最低価格、取引量を把握し、次の終値を予測します。私のニューラル ネットワークに関する個人的な知識は平均的なものですが、皆様の批判や訂正を歓迎します。 このチュートリアルは、デジタル通貨定量取引プラットフォーム (www.fmz.com) の発明者である FMZ によって作成されました。コミュニケーションには QQ グループ (863946592) への参加を歓迎します。

2. データと参考文献

関連する価格予測の例: https://yq.aliyun.com/articles/538484 RNN モデルの詳細な紹介: https://zhuanlan.zhihu.com/p/27485750 RNN の入力と出力を理解する: https://www.zhihu.com/question/41949741/answer/318771336 pytorch について: 公式ドキュメント https://pytorch.org/docs その他の情報は自分で検索してください。 また、この記事を理解するには、パンダ・クローラー・データ処理など、ある程度の前提知識が必要ですが、知らなくても問題ありません。

3. PyTorch LSTMモデルのパラメータ

LSTM のパラメータ:

最初にこの文書に密集したパラメータを見たときの私の反応は次のようなものでした。 ゆっくり読んでいくうちに、やっと理解できました。

input_size: 入力ベクトル x の特徴サイズ。終値を使用して終値を予測する場合は、input_size=1 になります。終値を高値で開始し安値で終了することを予測する場合は、input_size=4 になります。 hidden_size: 隠しレイヤーのサイズ num_layers: RNNの層数 batch_first: True の場合、最初の入力ディメンションは batch_size です。このパラメータも非常にわかりにくいため、以下で詳しく説明します。

入力データパラメータ:

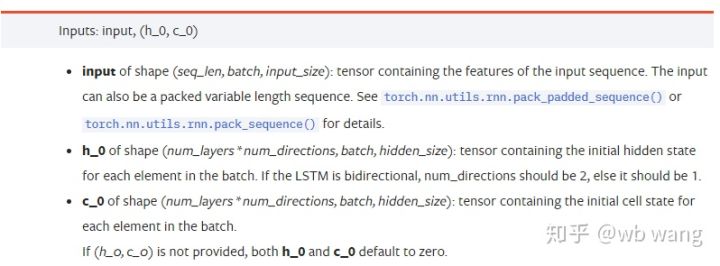
input: 特定の入力データは、(seq_len、batch、input_size) の特定の形状を持つ 3 次元テンソルです。このうち、seq_lenはシーケンスの長さ、つまりLSTMが考慮する必要がある履歴データの長さを指します。これはデータの形式のみを指し、LSTMの内部構造を指すものではないことに注意してください。同じLSTMモデルでも、異なる seq_len を持つ入力データを使用して予測を行うことができます。結果; batch はバッチ サイズを指し、データの異なるグループがいくつあるかを表します。input_size は以前の input_size です。 h_0: 初期の隠れ状態、形状は (num_layers * num_directions、batch、hidden_​​size)、双方向ネットワークの場合は num_directions=2 c_0: セルの初期状態。形状は上記と同じで、指定しないこともできます。

出力パラメータ:

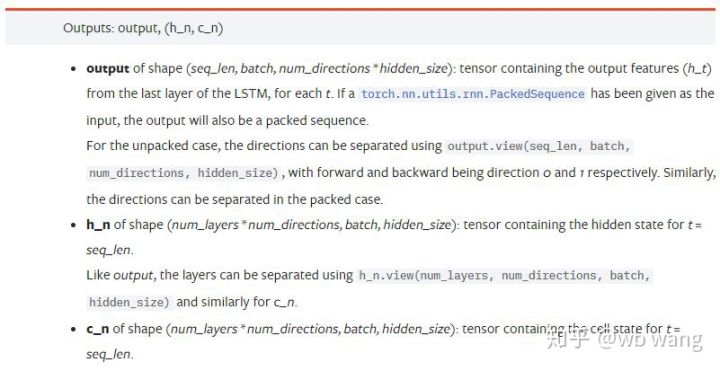
output: 出力形状（seq_len、batch、num_directions * hidden_​​size）、モデルパラメータbatch_firstに関連していることに注意してください。 h_n: 時刻 t = seq_len における h の状態、h_0 と同じ形状 c_n: 時刻 t = seq_len における c の状態、c_0 と同じ形状

4. LSTM入力と出力の簡単な例

まず必要なパッケージをインポートします

import pandas as pd
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

LSTMモデルの定義

LSTM = nn.LSTM(input_size=5, hidden_size=10, num_layers=2, batch_first=True)

入力データの準備

x = torch.randn(3,4,5)
# x的值为:
tensor([[[ 0.4657,  1.4398, -0.3479,  0.2685,  1.6903],
         [ 1.0738,  0.6283, -1.3682, -0.1002, -1.7200],
         [ 0.2836,  0.3013, -0.3373, -0.3271,  0.0375],
         [-0.8852,  1.8098, -1.7099, -0.5992, -0.1143]],

        [[ 0.6970,  0.6124, -0.1679,  0.8537, -0.1116],
         [ 0.1997, -0.1041, -0.4871,  0.8724,  1.2750],
         [ 1.9647, -0.3489,  0.7340,  1.3713,  0.3762],
         [ 0.4603, -1.6203, -0.6294, -0.1459, -0.0317]],

        [[-0.5309,  0.1540, -0.4613, -0.6425, -0.1957],
         [-1.9796, -0.1186, -0.2930, -0.2619, -0.4039],
         [-0.4453,  0.1987, -1.0775,  1.3212,  1.3577],
         [-0.5488,  0.6669, -0.2151,  0.9337, -1.1805]]])

xの形状は(3,4,5)です。batch_first=Trueこのとき、batch_size は 3、sqe_len は 4、input_size は 5 です。 x[[0]は最初のバッチを表します。

batch_first が定義されていない場合はデフォルトで False に設定され、データはバッチ サイズ 4、sqe_len 3、input_size 5 で完全に異なる方法で表現されます。現時点ではx[0]はt=0におけるすべてのバッチのデータを表します。個人的にこの設定は直感的ではないと感じたので、パラメータを追加しましたbatch_first=True.

2 つの間でのデータの変換も非常に便利です。x.permute(1,0,2)

入出力

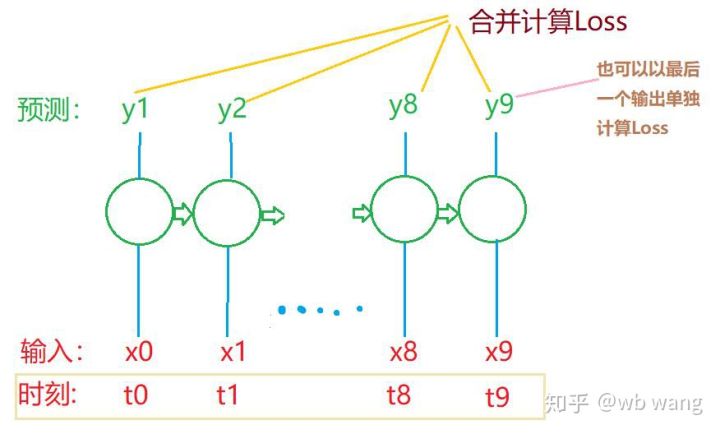
LSTM の入力と出力の形状は混同しやすいので、次の図を参考にしてください。
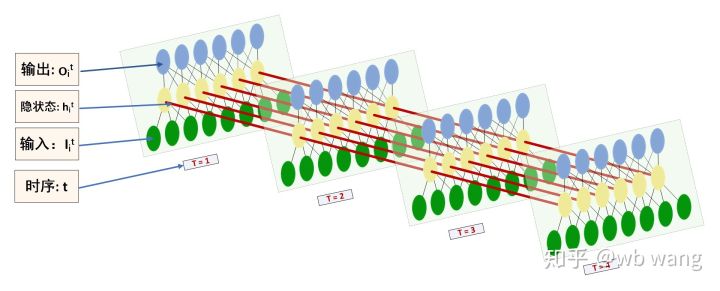
出典: https://www.zhihu.com/question/41949741/answer/318771336

x = torch.randn(3,4,5)
h0 = torch.randn(2, 3, 10)
c0 = torch.randn(2, 3, 10)
output, (hn, cn) = LSTM(x, (h0, c0))
print(output.size()) #在这里思考一下,如果batch_first=False输出的大小会是多少?
print(hn.size())
print(cn.size())
#结果
torch.Size([3, 4, 10])
torch.Size([2, 3, 10])
torch.Size([2, 3, 10])

前のパラメータの説明と一致する出力結果を確認します。 hn.size() の 2 番目の値が 3 であることに注意してください。これは batch_size のサイズと一致しており、hn には中間状態が保存されず、最後のステップのみが保存されることを示しています。 LSTMネットワークは2層なので、hnの最後の層の出力は実際には出力の値であり、出力の形状は[3, 4, 10]は、t=0,1,2,3のすべての瞬間の結果を保存するので、次のようになります。

hn[-1][0] == output[0][-1] #第一个batch在hn最后一层的输出等于第一个batch在t=3时output的结果
hn[-1][1] == output[1][-1]
hn[-1][2] == output[2][-1]

5. ビットコイン市場データを準備する

これまで述べてきたことの多くは、単なる前置きに過ぎません。LSTMの入力と出力を理解することは非常に重要です。そうでないと、インターネットからランダムにコードをコピーすると間違いを犯しやすくなります。時系列の LSTM では、モデルが間違っていても、最終的には取得できます。良い結果です。

データ収集

使用されるデータは、Bitfinex取引所のBTC_USD取引ペアの市場データです。

import requests
import json

resp = requests.get('https://q.fmz.com/chart/history?symbol=bitfinex.btc_usd&resolution=15&from=0&to=0&from=1525622626&to=1562658565')
data = resp.json()
df = pd.DataFrame(data,columns = ['t','o','h','l','c','v'])
print(df.head(5))

データ形式は次のとおりです。

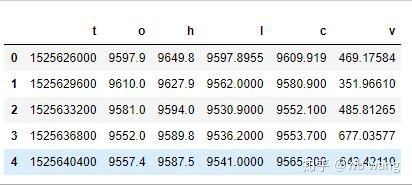
データ前処理

df.index = df['t'] # index设为时间戳
df = (df-df.mean())/df.std() # 数据的标准化,否则模型的Loss会非常大,不利于收敛
df['n'] = df['c'].shift(-1) # n为下一个周期的收盘价,是我们预测的目标
df = df.dropna()
df = df.astype(np.float32) # 改变下数据格式适应pytorch

データ標準化の方法は非常に大まかで、いくつかの問題があります。これはデモンストレーション用です。yield などのデータ標準化を使用できます。

トレーニングデータの準備

seq_len = 10 # 输入10个周期的数据
train_size = 800 # 训练集batch_size
def create_dataset(data, seq_len):
    dataX, dataY=[], []
    for i in range(0,len(data)-seq_len, seq_len):
        dataX.append(data[['o','h','l','c','v']][i:i+seq_len].values)
        dataY.append(data['n'][i:i+seq_len].values)
    return np.array(dataX), np.array(dataY)
data_X, data_Y = create_dataset(df, seq_len)
train_x = torch.from_numpy(data_X[:train_size].reshape(-1,seq_len,5)) #变化形状,-1代表的值会自动计算
train_y = torch.from_numpy(data_Y[:train_size].reshape(-1,seq_len,1))

train_xとtrain_yの最終的な形状は次のようになります: torch.Size([800, 10, 5]), torch.Size([800、10、1]）。私たちのモデルは 10 期間のデータに基づいて次の期間の終値を予測するため、理論的には 800 バッチで 800 の予測終値のみが必要になります。しかし、train_y には各バッチに 10 個のデータがあります。実際、最後の結果だけでなく、各バッチ予測の中間結果も保持されます。最終的な損失を計算するときは、10 個の予測結果すべてを考慮に入れて、train_y の実際の値と比較することができます。理論的には、最後の予測結果の損失のみを計算することも可能である。この問題を説明するために大まかな図を描きました。 LSTM モデルには実際には seq_len パラメータが含まれていないため、モデルをさまざまな長さに適用でき、中間予測結果も意味があるため、Loss の計算をマージする傾向があります。

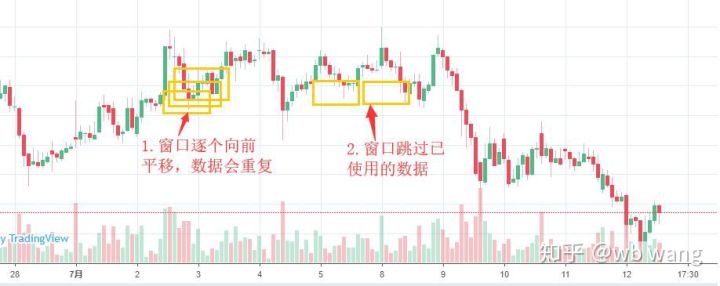
トレーニングデータを準備する際、ウィンドウの移動がぎくしゃくしていて、使用されていたデータが使用されなくなることに注意してください。もちろん、ウィンドウを1つずつ移動することもできるので、得られるトレーニングセットははるかに大きくなります。 。しかし、隣接するバッチデータが重複しすぎると感じたため、現在の方法を採用しました。

6. LSTMモデルの構築

最終モデルは次のようになります。これには 2 層の LSTM と線形層が含まれます。

class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, output_size=1, num_layers=2):
        super(LSTM, self).__init__()
        self.rnn = nn.LSTM(input_size,hidden_size,num_layers,batch_first=True)
        self.reg = nn.Linear(hidden_size,output_size) # 线性层,把LSTM的结果输出成一个值

    def forward(self, x):
        x, _ = self.rnn(x) # 如果不理解前向传播中数据维度的变化,可单独调试
        x = self.reg(x)
        return x
        
net = LSTM(5, 10) # input_size为5,代表了高开低收和交易量. 隐含层为10.

7. モデルのトレーニングを開始する

ようやくトレーニングが開始されました。コードは次のとおりです。

criterion = nn.MSELoss() # 使用了简单的均方差损失函数
optimizer = torch.optim.Adam(net.parameters(),lr=0.01) # 优化函数,lr可调
for epoch in range(600): # 由于速度很快,这里的epoch多一些
    out = net(train_x) # 由于数据量很小, 直接拿全量数据计算
    loss = criterion(out, train_y)
    optimizer.zero_grad()
    loss.backward() # 反向传播损失
    optimizer.step() # 更新参数
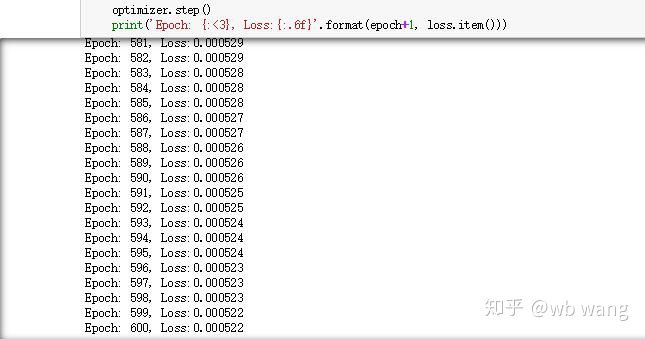
    print('Epoch: {:<3}, Loss:{:.6f}'.format(epoch+1, loss.item()))

トレーニング結果は次のとおりです。

8. モデル評価

モデルの予測値は次のとおりです。

p = net(torch.from_numpy(data_X))[:,-1,0] # 这里只取最后一个预测值作为比较
plt.figure(figsize=(12,8))
plt.plot(p.data.numpy(), label= 'predict')
plt.plot(data_Y[:,-1], label = 'real')
plt.legend()
plt.show()

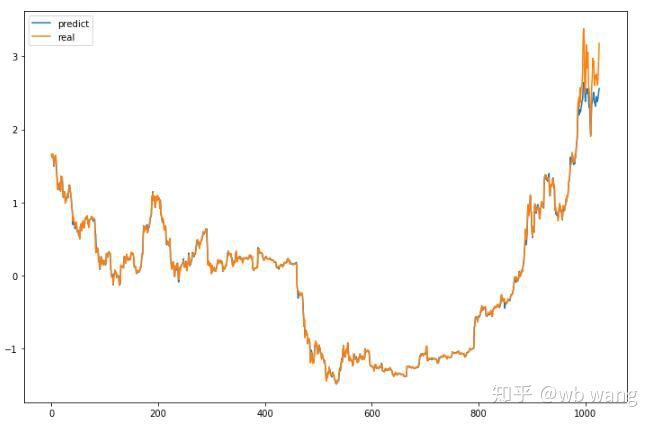
図からわかるように、訓練データ（800以前）の適合度は非常に高いが、ビットコインの価格はその後新たな高値に上昇しており、モデルはこれらのデータを見たことがないので、予測はうまくパフォーマンスできない。これは、以前のデータ標準化に問題があったことも示しています。 予測価格は正確ではないかもしれませんが、上昇と下降の予測はどの程度正確でしょうか? 予測データの一部を見てみましょう。

r = data_Y[:,-1][800:1000]
y = p.data.numpy()[800:1000]
r_change = np.array([1 if i > 0 else 0 for i in r[1:200] - r[:199]])
y_change = np.array([1 if i > 0 else 0 for i in y[1:200] - r[:199]])
print((r_change == y_change).sum()/float(len(r_change)))

上昇と下降の予測精度は81.4％に達し、期待を上回る結果となりました。どこかで間違いを犯したかどうかは分かりません。

もちろん、このモデルに実質的な価値はありませんが、シンプルで理解しやすいものです。これを出発点として使ってください。デジタル通貨の定量化におけるニューラル ネットワークの応用に関する入門コースは今後も増えていく予定です。