ニュートラル・ヘッジ統計仲裁 新品 純アルファ・ドリーム版

中立ヘッジ・スタット・アービトレイジ 新 ((純アルファ・ドリーム・エディション)

- 長期・短期負債を0つ持てる強力なアビトレージ戦略

こんにちは,すべてのトレーダー,数ヶ月間デバッグ,最適化,繰り返しを経て,この中立ヘジング統計的アービタージがより安定したレベルに達し,あなたと一緒に見ることができることを非常に嬉しく思います. これは長期ショートヘジングに基づいた市場中立戦略です.同じ口座の品種バスケットでロングと品種バスケットでショートに行く場合,ロングとショート値は等しいです. 市場におけるベータシステムリスクを回避するという前提で,統計的方法は,アルファ安定した収益性の低リスクの長期ショートマッチング組み合わせを見つけるために使用されます. この戦略は,市場との低相関,中立長期ショート露出,および31/5219などの極端なブラックスワンの下でのリスクがない良好な保有経験を持っています. その代わりに,このような価格設定の誤差が混沌としたときに市場が繁栄します. この戦略は完全に詳細に説明されます.

こんにちは! 私のチャンネルへようこそ!

私は量子開発者です.私はフルスタックCTA&HFT&Arbitrageおよび他の取引戦略を開発しています. FMZのプラットフォームのおかげで,私は私の量的なチャンネルで量的な開発に関連するより多くのコンテンツを共有し,量的なコミュニティの繁栄を維持するためにすべてのトレーダーと協力します.

詳しくは,私のチャンネルに移動してください~ 私はここであなたを待っていますトレーダーマン・ホーム

1. 統計的仲裁の導入と説明

統計的仲介戦略は,異なるバスケット品種間の価格関係を取引のために利用する戦略である.この戦略は,統計的原則に基づい,歴史上の価格動向と2つ以上の品種間の相関を分析し,それらの間の価格差異を見つけ,これらの差異を取引に使用する.歴史的に,クロス・スペイスペアリング統計的仲介戦略は,株式市場で広く使用されている.最も初期のクロス・スペイス仲介戦略は,主に石油会社や通信会社などの同じ業界または関連産業の株式間で実施された.これらの戦略は,しばしば業界相関の仮定に基づいており,過大評価の株式を購入し,過大評価の株式を売ることで仲介の目的を達成する.

市場の発展とともに,クロス・スペイスマッチング統計的仲介戦略は,商品先物,外為,仮想通貨などの他の金融市場にも徐々に拡大している.これらの市場では,異なるバスケット組み合わせが関連しており,価格差を使用して仲介取引を行うことができる.この戦略の論理は平均逆転の原則に基づいている.構築された複数のバスケット組み合わせの価格が統計の範囲から逸脱すると,レグレッション傾向がある.この傾向によると,価格が大きく逸脱すると,市場の短期的誤価化からヘッジするために高価格の品種のバスケットを売り,低価格の品種のバスケットを購入することができます.この方法で,マルチバスケットペアの組み合わせの拡散から利益を得ることができます.

2. 統計仲裁 の 利点 と 欠点

利点:

• 市場リスクを軽減する:統計的仲介戦略は,さまざまなバスケット製品組合せの違いに基づく仲介取引に基づいています.単一製品取引と比較して,リスクを分散させ,市場変動の戦略への影響を軽減します.市場のシステムリスクを軽減します.
• 安定収入:統計的仲介戦略は,短期間の市場誤価化に対して回帰仲介取引を行う.方向的戦略と比較して,より安定した収入特性を有する.方向的戦略と比較して,リスクが低く,変動が低く,安定した収益を生み出します.
• 異なる市場環境に適応できる: 統計的仲介戦略は,この取引戦略が市場と方向的な関係が少ないため,異なる市場環境で動作することができる.

欠点:

• 歴史的データは過去関係のみを反映し,将来を完全に表現することはできないため,一定のリスクがある.統計的仲介戦略の構築は,歴史的なビッグデータに基づくバスケット品種の組み合わせと相関を採掘するために多数の統計テストを使用する.将来に変化が起こり,特定のリスク管理措置が必要である.
• 市場における短期的な価格設定の誤りにより,バランス関係に戻るのに必要な時間を正確に判断するのは困難です.取引時間があまりにも長くなった場合,資金の使用コストも非常に高くなります.
• 高度なデータ分析とモデル構築能力: 統計アビラージ戦略には,異なるバスケット組み合わせ間の相関と共同統合などの統計データの詳細な分析とモデリングが必要であり,高いデータ分析とモデル構築能力が必要です.
• トランザクション実行および流動性リスク:クロス・バラエティ取引であるため,実行価格と取引量は異なるバラエティによって影響され,トランザクション実行リスクがあります.より洗練された戦略設計とアーキテクチャ実装が必要です.

3. このアルファ統計的アービタージの主な内容

**1,すべての種類のデータ情報をリアルタイムでモニターし,ビッグデータスキャンを行い,長と短い種類のバスケット組み合わせを構築します. **

具体的には,バスケット組み合わせが構築される.例えば,A,B,C,D,E,Fの6種類がある場合,それぞれ3種類ずつ2つのグループに分割してバスケット組み合わせを構築することができる.同時に,インデックス・アビタージも構築される.いくつかの産業や部門の種類を2つに分割し,2つの新しい市場インデックスを構築し,次にこれらの2つのインデックスに関する統計データ分析を行う.

**2,長いバスケットと短いバスケットの組み合わせの相関をテストする. **

関連性とは,二つ以上の変数との関連度を指す.ある変数と別の変数の変化の間の関係を測定するために使用され,特定の対応性があるかどうかを判断したり,ある変数で変化が他の変数に与える影響を予測するのに役立ちます.関連性係数は,関連性を測定するための一般的な方法です.一般的なものは,ピアソン関連性系数,スピーマンのランク関連性系数などです.ピアソン関連性系数は,2つの連続変数間の関係を評価し,スピーマンのランク関連性系数は,2つの順序変数間の関係を評価するのに適しています.

関連系数の値範囲は [-1, 1] で,−1 は負の相関,−1 は正の相関,−0 は相関がないことを示します.相関系数が−1 または−1 に近いほど相関が強く,0 に近いほど相関が弱くなります.相関系数の数学式は以下のとおりです (ピアソン相関系数を例として):

r = cov ((X,Y) / (std ((X) * std ((Y)).

関連性テストでは,共通的なアプローチは,関連性テストの統計的意味を計算することです. 仮説テストは,通常,関連性テストが有意かどうかを判断するために使用できます. 仮説テストのゼロ仮説は,変数間の関連性がないことであり, nul仮説を拒否するかどうかを決定するために,関連性テストの統計が計算されます.

**3 長い/短いバスケットの組み合わせの共同統合を試験する. **

コインテグレーションとは,2つ以上の時間系列変数間の長期間の関係,すなわちそれらの線形組み合わせが安定していることを指す.コレレーションと比較して,コインテグレーションは,短期間の相関度よりも長期間の均衡関係により多くの注意を払っている.この均衡関係から逸脱すると,偏差を合理的な範囲に戻す修正メカニズムがある.コインテグレーションの概念は,当初,1987年にスピーゲルマン (S.G.エンゲル) とC.W.J.グランジャー (C.W.J.グランジャー) によって,時間系列分析に存在する虚偽回帰問題を解決するために提案された.偽回帰問題は,変数間の単位根の存在の可能性によって引き起こされる.単位は,変数間の回帰関係が短期間の均衡根に有意に見えるが,長期間の実際の関係はない.

コインテグレーション理論は,時間系列の非静止性を分析することから始まり,非静止変数に含まれる長期均衡関係を探求する.関係する変数が最初の差後に静止し,これらの変数の一定の線形組み合わせが静止している場合,これらの変数の間にコインテグレーションが存在すると言われます.コインテグレーションは2つ以上のシリーズ間の静止関係を記述するために使用されます.各シーケンス個別に,それは非静止である可能性があります.これらのシーケンスの中間値,変数または共変数などの瞬間は時間とともに変化しますが,これらの時間系列の線形組み合わせシーケンスには時間とともに変化しない性質がある可能性があります.二つの資産の価格がコインテグレーション関係に従うとき,それらの線形組み合わせは平均逆転の性質を満たします.コインテグレーションの数学的式は以下の通り表されます (時間系列の2つの変数を例として):

Y_t = β_0 + β_1 * X_t + ε_t

Y_tとX_tは,それぞれ2つの時間列変数の観測値を表し,β_1は回帰係数, ε_tは誤差項である.Y_tとX_tの間に共積分関係がある場合,両変数の線形組み合わせは安定する,すなわち ε_tは静止である.平均値0で正規分布を満たす.共積分をテストする際には,通常安定性テストが必要である.一般的に使用される方法には,ヨハンセンテストとエンゲル・グレンジャーテストが含まれている.ヨハンセンテストは自有値に基づく方法であり,複数の変数の間の共積分を直接テストすることができる.エンゲル・グレンジャー2段階テストは,修正されたOLS推定 (普通最小平方) をベースとした方法であり,二つの変数の間の共積分関係をテストするのに適している.

**4. この戦略では,多くの組み合わせに対する時間列の共同統合関係をテストする.具体的な基準は以下のとおりである: **

• 別々の組み合わせたバスケットの時間価格列は,第一順位積分ベクトルである.すなわち,時間価格列は静止性がない (明らかな傾向がある).複数の時間価格回の静止性をテストするために,ADF単位根を使用する.
• 個々の組み合わせたバスケットの最初の差の後のシリーズ (すなわち派生) は静止している. 2つのバスケット時間価格シリーズをテストするためにADF単位根を使用する. 2つのバスケットの時間価格シリーズの最初の差の静止性をテストするためにADF単位根を使用する.
• 偶数組み合わせの時間値系列の特定の線形組み合わせは静止である.つまり,2つのシリーズから構成された線形方程式の残りは静止である.同じ順序の2つの配列に対して,OLS回帰を実行し,残数の静止性をテストする.

**5 ハーストインデックステストを大量に実施する **

ハースト指標は,一連の平均逆転特性を決定するために,時間系列の長期記憶量を測定するために使用される. ハースト指標値は0から1の間であり,0.5に近い値は,配列がランダムなウォークを示し,1に近い値は持続的な傾向を示している.原則: ハースト指標は,配列の重なるサブシーケンスの分散範囲とその長さの間の関係を計算することによって,配列の長期記憶の程度を推定する.数学式: ハースト指標を計算する1つの方法は,重なるサブシーケンスの分散範囲と長さの間の関係を利用して,ランダムなウォークの対応関係を確立することです. ハースト指標は,重なるサブシーケンスの分散範囲と長さの間の線形回帰を使用して推定することができます.

**6 平均逆転半減期推定 **

平均逆転半減期 (mean reversion half-life) は,価格シリーズが平均に戻るのにかかる時間を推定するために使用される指標である. 半減期が小さいほど,平均逆転が速くなります. 原則: 平均逆転半減期の計算は,収束指数式滑らかな移動平均モデル (EMA) に適合することによって推定されます. 価格シリーズが平均から半減期以上逸脱すると,平均逆転の機会があると考えることができます. 数学的式: 平均逆転半減期の計算式は以下のとおりです:

(H = -\frac{\ln(0.5)}{\ln(\frac{P_t}{P_t - P_{t-1}}})

試験方法: 価格シリーズの EMA を計算し,その後 EMA をベースに半減期を計算できます.

**7. 膨大な統計データに基づいて取引戦略を構築する. **

ハースト指数整理に基づくフィルターバスケット製品組み合わせ,平均リバーション半減期に基づいて関連するパラメータを推定し,統計的共同統合に基づく取引戦略組み合わせを構築します. x と y が資産の価格時間系列であると仮定します.

コインテグレーションテストの後,資産XとYの時間価格の間にコインテグレーション関係があることが判明.残留項cの標準偏差は σであり,定数 λが境界値として選択される.

• lny-(a+blnx) > λσの場合,バスケットYの価格は比較的過大評価され,バスケットXの価格は比較的過小評価されます.バスケットXを買い,バスケットYを売ります.
• lny- ((a+blnx) < -λσの場合,バスケットXの価格は比較的過大評価され,バスケットYの価格は比較的過小評価されます.バスケットYを購入し,バスケットXを販売します.
• 価格差 lny- ((a+blnx) が [-0.5λσ, 0.5λσ] のような一定範囲に戻ると,ポジションは閉じる.

8番目,もっと来ます

より独占的で革新的なロジック,より詳細なアーキテクチャ,詳細な処理は,独自の核心競争力です.現在,流動性は統計的に推定され,取引は市場価格を使用して完了します.将来,それは徐々に等待中の注文タイプの高周波統計的仲裁に繰り返しアップグレードされます.私たちは注目して一緒に成長することを楽しみにしています.

4. 部分的な過去業績 (実際の取引価格を推定した後の5万件の注文のコストデータ)

中立ヘジング統計仲裁 新・スーパースター

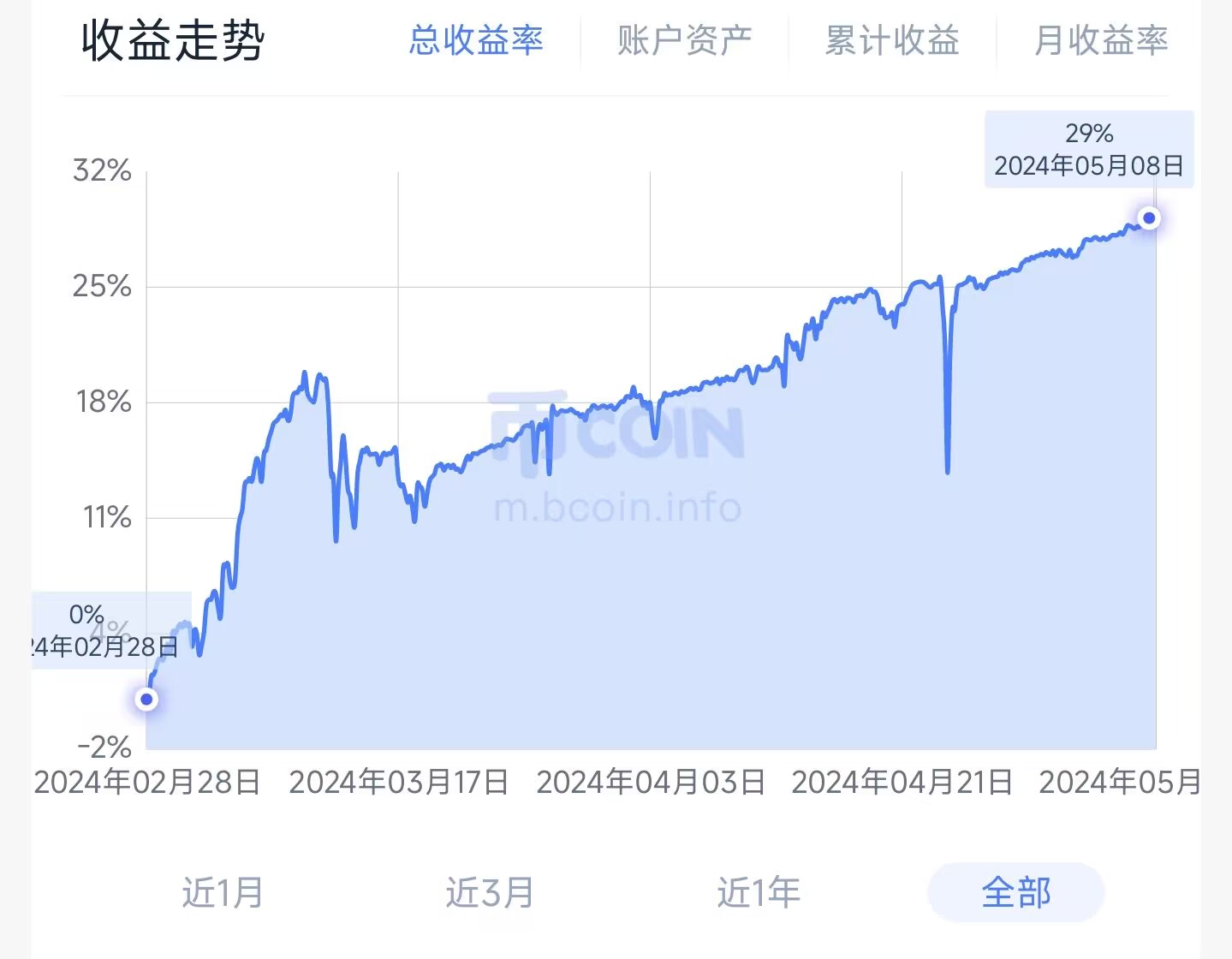
5. 協力,交流,共同学習と進歩を期待する

どんな戦略にも独自の方法論と適性があります.例えば,平均逆転戦略は市場ランダムウォークや他の理論に基づいています.モメントトレンド戦略は,市場の脂肪尾変動などのさまざまな行動金融理論に基づいています.我々はその原則を理解し,その特徴に基づいて変動に適応する必要があります.同時に,戦略のユーザーは,利益と損失の同じ源に注意を払わなければならない.高い収益は,より高いリスクに伴わなければならない.成熟した戦略には利点と欠点があります.彼らは合理的にそれらを使用し,強みを最大化し,弱点を避ける必要があります.彼らが正しいか間違っているか,そして市場状況に応じて適切であるか否かを知ることです.完全なパフォーマンス,自信を持って,驚かないでください.

定量化 は 永遠 の 機械 で は あり ませ ん.また 全能 で も あり ませ ん.しかし,それ は 将来 の 取引 の 方向 で ある べき で あり,あらゆる トレーダー が 学ぶ 価値 が あり,使わ れ ます!トレーダー は 来て 欠点 を 指摘 し,一緒に 議論 し,学び,一緒に 進歩 し,壮大な 市場 の 風 と 波 を 乗り,前進 する よう 歓迎 さ れ ます.

● 賃貸 プラン: XXXU/XU/月,現在 の 優遇 期間 は 賃貸 は 無料 で あり,いつでも 終了 できる.

● 分担 計画: 大額 の 事業 を 無料 に 始め られ,利潤 の 20% が 月々 に 抽出 さ れ ます.利潤 が ない 場合,利潤 は 分担 さ れ ませ ん.

●戦略的コミットメント:利用者がリース期間の終わりに利益を上げ,コストをカバーしない場合 (構成とパラメータが正しければ,不可抗力によるブラック・スワンではありません) は,利益を得るまで無条件に1ヶ月を与えられます.

● より多くの協力の選択肢:必要のある個人や機関のためにです.私たちは皆,協力に対してオープンで双方の利益を得る姿勢を維持し,お客様のニーズやリスクの優先順位などに基づいて,議論とカスタマイズされた協力を楽しみにしています.

短期間の利益や損失などのリスクが高く 短期間の取引の必要性がある場合は 3〜50%の月額収益率で 清算リスクがない 別の安定した高頻度戦略をチェックできます 高周波ヘージング 市場作りグリッド 新 (HFT市場作りマイニングマシンバージョン)

**あなたが多くの資金を持っている場合,あなたは,実際の取引の900日間,雨や日光,持続する,大容量の中低周波複合CTA取引システムを見ることができます.それは最も長い歴史,高い安定性と強い普遍性を持つCTA戦略組み合わせシステムです.現在,中長期の安定した成長を達成するために発表されています: **複合 CTA トレーディング システム 新 ((多要素+多種類+多戦略公開版)

連絡先情報 (コミュニケーションと議論,学び,共同で進歩するために歓迎します) ハイヤニッズ テレグラム:https://t.me/JadeRabbitcmもっと役立つ情報 トレードマンホーム:https://www.fmz.com/market-offer/512 完全自動CTA&HFT&仲裁取引システム @2018 - 2024

もっと