KNN 알고리즘을 기반으로 한 베이지안 분류기

분류기의 분류 결정을 위한 설계 이론의 기초 베이지 결정 이론:

비교 P(ωi 11:1x) ᅳ 여기서ωi 는 제1등급, x 는 관찰되고 분류해야 하는 데이터이다, P(ωi 11:1x) 는 이 데이터의 특징 변수가 알려져 있는 상태에서, 그것이 제1등급에 속하는 것을 판단하는 확률이 얼마나 되는지 나타낸다. 이것은 또한 후진 확률이 된다. 베이스 공식에 따르면, 다음과 같이 나타낼 수 있다:

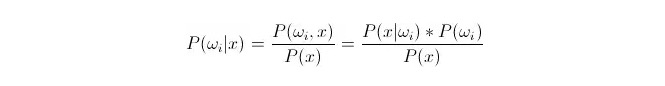
그 중 P ((xfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latnfin_Latn) i) on samankaltaisuuden todennäköisyys, P ((ωi) on a priori todennäköisyys, 왜냐하면 a priori todennäköisyys on a priori todennäköisyys.

분류할 때, 주어진 x, 후검 확률 P ((ωigadgadx) 가 가장 큰 범주를 선택할 수 있다. 비교할 때 각 범주 아래 P ((ωigadx) 가 크면,ωi는 변수이고, x는 고정되어 있다. 따라서 P (((x) 를 제거하고, 고려하지 않는다.

그래서 P (x) 는 P (x) 입니다.*P ((ωi) 의 질문 선전 확률 P ((ωi) 는 통계 훈련중심의 각 분류하에서 나타나는 데이터의 비율이 충분하다.

유사 확률 P ((x Berdosaωi) 의 계산은 번거롭다. 왜냐하면 이 x는 테스트 집합의 데이터이기 때문에, 훈련 집합에 따라 직접적으로 얻을 수 없다. 그러면 우리는 훈련 집합 데이터의 분포 법칙을 찾아내야 하고, 그러면 P ((x Berdosaωi) 를 얻을 수 있다.

다음은 k 근접 알고리즘, 영어로는 KNN이다.

우리는 훈련중심의 데이터 x1,x2…xn (각 데이터가 m 차원) 에 따라, 범주ωi에서, 이러한 데이터의 분포를 맞추고자 합니다. x를 m 차원 공간의 임의의 점으로 설정하여, 어떻게 P ((x값ωi) 를 계산합니까?)

우리는 데이터가 충분히 많을 때 비례적으로 근사 확률을 사용할 수 있다는 것을 알고 있다. 이 원칙을 이용하여, 점 x의 주변에서, 점 x에서 가장 가까운 k개의 샘플 포인트를 찾아내는데, 그 중 카테고리 i에 속하는 것이 있다. 이 k개의 샘플 포인트를 둘러싸고 있는 최소 초구 (超球) 의 부피 V를 계산하고, 또 모든 샘플 데이터에서 ωi에 속하는 숫자를 찾아내면:

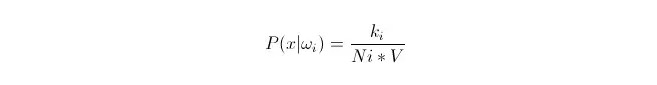
그리고 우리가 실제로 계산한 것은 x의 클래스 조건 확률 밀도입니다.

P (ωi) 는 어떻게 될까요? 위의 방법을 따르면, P ((ωi) = Ni/N 。 여기서 N은 샘플의 총수 。 그리고 P (x) = k (n)*V), 여기서 k는 이 초구체를 둘러싸고 있는 모든 샘플 포인트의 개수; N은 샘플의 총수이다. 그래서 P (ωi 11:3x) 는 계산할 수 있습니다.

P(ωi|x)=ki/k

위의 식을 설명하자면, V 크기의 초구체 안에, k 개의 샘플을 둘러싸고, 그 중 i 계열의 k 가 있다. 이렇게, 둘러싸고 있는 어떤 종류의 샘플이 가장 많고, 우리는 여기서 x가 어떤 계열에 속해야 하는지를 결정할 수 있다. 이것이 k 근접 알고리즘으로 설계된 분류기이다.