파이썬 단순 베이어스 응용 프로그램

예측 변수들 사이의 상호 독립성을 전제로 하여, 바에이즈 정리에 따라 순수 바에이즈 분류 방법을 얻을 수 있다. 더 쉽게 말해서, 순수 바에이즈 분류기는 분류의 다른 특성들과 관련이 없는 분류의 한 특성을 가정한다. 예를 들어, 만약 과일들이 둥글고 붉은 색이고, 지름이 약 3인치라면, 그 열매는 아마 사과일 것이다. 비록 그 특성이 서로 의존적이거나 다른 특성의 존재에 의존적이더라도, 순수 바에이즈 분류기는 각각의 특성을 독립적으로 암시하여 이 열매가 사과라는 것을 가정한다.

• 단순 베이어스 모델은 쉽게 만들 수 있으며, 큰 데이터 세트에서 매우 유용하다. 단순하지만 단순 베이어스 표현은 매우 복잡한 분류 방법을 초월한다.

  베이어스 정리는 P©, P (x) 와 P (x) 에서 추후실험 확률 P (c) 를 계산하는 방법을 제공합니다. 다음 방정식을 참조하십시오:

  

  이 곳에서는

  P (c) 는 알려진 예측 변수 (c) 의 (d) 특성을 가정하는 경우, 클래스 (d) 의 (d) 목표의 (d) 후의 확률이다. P©는 클래스의 전연 확률입니다. p (x) 는 확률, 즉 알려진 클래스의 전제에서 예측되는 변수의 확률입니다. P (x) 는 예측 변수의 전의 확률입니다. 예제: 이 개념을 한 예로 이해하도록 하자. 아래에는 날씨 훈련 세트와 그에 상응하는 목표 변수인 Play () 를 가지고 있다. 이제 우리는 날씨에 따라 놀고 있는 참가자와 놀지 않는 참가자를 분류해야 한다. 다음 단계를 수행하도록 하자.

  단계 1: 데이터 세트를 주파수 표로 변환합니다.

  단계 2: 오버캐스트의 확률이 0.29이고 플레이의 확률은 0.64일 때 비슷한 을 사용하여 확률 테이블을 만듭니다.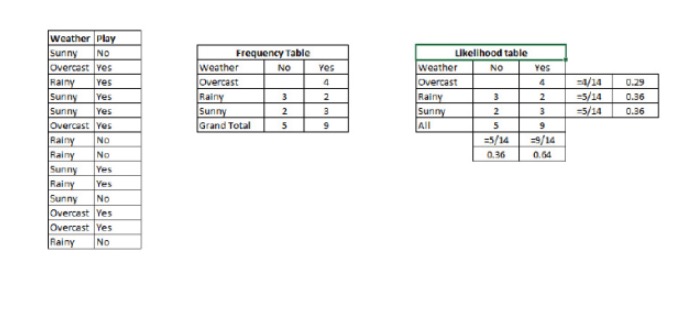

  

  단계 3: 이제 순수 바이에스 방정식을 사용하여 각 클래스의 후속 확률을 계산하십시오. 후속 확률이 가장 큰 클래스는 예측의 결과입니다.

  질문: 날씨가 좋다면 참가자들은 놀 수 있습니다.

  이 문제를 풀기 위해, 우리가 방금 논의한 방법을 사용해야 합니다. 그래서 P (놀이) = P (놀이) * P (놀이) / P (놀이)

  우리는 P를 가지고 있습니다 3/9 = 0.33, 5/14 = 0.36, 9/14 = 0.64.

  이제, P는 0.33 곱하기 0.64 / 0.36 = 0.60, 더 큰 확률이 있습니다.

  순수한 베이어스는 비슷한 방법을 사용하여 다른 속성을 통해 다른 범주의 확률을 예측합니다. 이 알고리즘은 일반적으로 텍스트 분류와 여러 범주를 포함하는 문제에 사용됩니다.

• 파이썬 코드:

#문서관 수입 sklearn.naive_bayes에서 GaussianNB를 가져옵니다. # 당신이 가지고 있다고 가정, X (예측자) 및 Y (목적) 훈련 데이터 세트 및 x_test (예측자) 의 test_dataset

SVM 분류 객체 모델 = GaussianNB를 생성합니다.

베르누일리나이브 베이즈, 참조 링크와 같은 다항식 클래스의 다른 분포가 있습니다.

훈련 세트를 사용하여 모델을 훈련하고 점수를 확인

model.fit(X, y) #출력 예측 예측= 모델.예측 (x_test)