Aplikasi Python Bayes yang sederhana

Berdasarkan teorema Bayesian, pemeringkat sederhana Bayesian boleh diperoleh dengan asumsi bahawa variabel yang diprediksi adalah bebas antara satu sama lain. Dengan kata yang lebih mudah, pemeringkat sederhana Bayesian menganggap ciri-ciri pemeringkat tidak berkaitan dengan ciri-ciri lain dalam pemeringkatannya. Sebagai contoh, jika buah bulat dan merah, dan diameternya kira-kira 3 inci, maka buah itu mungkin epal. Walaupun ciri-ciri ini bergantung kepada satu sama lain, atau bergantung kepada kehadiran ciri lain, pemeringkat sederhana Bayesian akan menganggap ciri-ciri ini secara berasingan menunjukkan bahawa buah itu adalah epal.

• Model Bayesian sederhana mudah dibina dan sangat berguna untuk set data yang besar. Walaupun mudah, persembahan Bayesian sederhana melampaui kaedah klasifikasi yang sangat rumit.

  Bayes' theorem menyediakan satu kaedah untuk mengira kebarangkalian P (c) dari P©, P (x) dan P (x) c. Sila lihat persamaan berikut:

  

  Di sini,

  P (c) adalah kebarangkalian masa depan bagi kelas (target) dengan syarat bahawa pemangkin (properties) pemboleh ubah diketahui P© adalah kebarangkalian terdahulu kelas. P adalah kebarangkalian, iaitu kebarangkalian, bagi pemboleh ubah yang meramalkan dalam keadaan kelas yang diketahui. P (x) adalah kebarangkalian terdahulu bagi pembolehubah Contoh: Mari kita gunakan satu contoh untuk memahami konsep ini. Di bawah ini, saya mempunyai set latihan cuaca dan pemboleh ubah sasaran yang sesuai. Sekarang, kita perlu mengklasifikasikan peserta yang akan bermain permainan dan yang tidak bermain permainan berdasarkan keadaan cuaca. Mari kita lakukan langkah-langkah berikut.

  Langkah 1: Mengubah dataset kepada jadual frekuensi.

  Langkah 2: Membuat jadual kebarangkalian dengan menggunakan peluang permainan seperti 0.64 jika kemungkinan Overcast adalah 0.29.

  

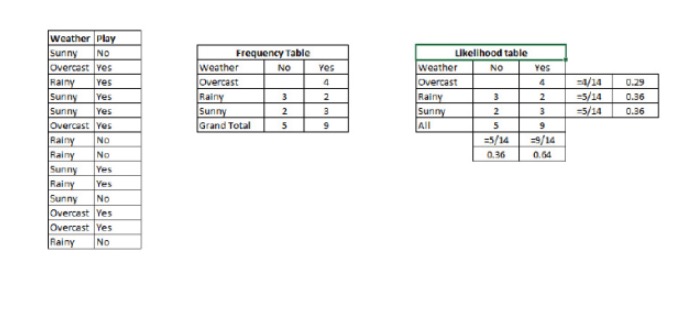
  Langkah 3: Sekarang, gunakan persamaan Bayes yang sederhana untuk mengira kebarangkalian akhir bagi setiap kelas. Kelas dengan kebarangkalian akhir terbesar adalah hasil daripada ramalan.

  Soalan: Jika cuaca cerah, peserta boleh bermain. Adakah kenyataan ini benar?

  Kita boleh selesaikan masalah ini dengan menggunakan kaedah yang kita bincangkan di atas. Jadi P (bermain) = P (bermain) * P (bermain) / P (bermain)

  Jadi kita mempunyai P = 3/9 = 0.33, dan P = 5/14 = 0.36, dan P = 9/14 = 0.64.

  Sekarang, P (akan bermain) = 0.33 kali 0.64 / 0.36 = 0.60, dengan kemungkinan yang lebih besar.

  Bayes yang polos menggunakan kaedah yang sama untuk meramalkan kemungkinan kategori yang berbeza melalui sifat yang berbeza. Algoritma ini sering digunakan untuk mengklasifikasikan teks, serta masalah yang melibatkan pelbagai kategori.

• Kod Python:

#Import Perpustakaan daripada sklearn.naive_bayes import GaussianNB # Mengandaikan anda mempunyai, X (predictor) dan Y (target) untuk latihan set data dan x_test(predictor) dari test_dataset

Buat model objek klasifikasi SVM = GaussianNB()

terdapat pembahagian lain untuk kelas multinomial seperti Bernoulli Naive Bayes, Refer link

Latih model menggunakan set latihan dan periksa skor

model.fit(X, y) #Prediksi Output diprediksi= model.predict ((x_test)