Classificador bayesiano baseado no algoritmo KNN

A base teórica para o design de classificadores para tomada de decisões de classificação Teoria da decisão de Zambeze:

Comparando P{\displaystyle i\,\!}, em que ωi é de classe i e x é um dado observado e a ser classificado, P{\displaystyle i\,\!} representa a probabilidade de um dado pertencer a classe i em função de um vetor característico conhecido, que também é a probabilidade de retrospectiva. De acordo com a fórmula de Bayes, pode ser representado como:

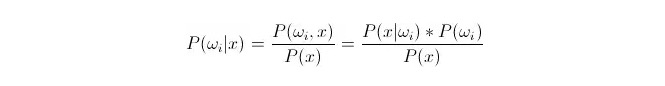
Dentre eles, P ((xfin_Latnfin_Latnfin_Latnfin_Latn) i) é chamado de probabilidade de similaridade ou probabilidade condicionalista; P ((ωi) é chamado de probabilidade antecipada, pois não está relacionado com a experiência e pode ser conhecido antes da experiência.

Na classificação, dado x, pode-se escolher a categoria que faz com que a probabilidade de retrospectiva P ((ωiⴰⵙx) seja maior. Quando P ((ωiⴰⵙx) é pequena sob cada categoria de comparação, ωi é variável e x é fixo; portanto, P ((x) pode ser excluído e não considerado.

Então isso se resume a calcular P (x) =*P ((ωi) questão A probabilidade de antecedência P ((ωi) é boa, desde que o treinamento estatístico se concentre na proporção de dados que aparecem sob cada classificação.

O cálculo da probabilidade P (x < i < i) é complicado, pois o x é o dado do teste, e não pode ser obtido diretamente com base no conjunto de treinamento. Então, precisamos encontrar a distribuição dos dados do conjunto de treinamento e obter P (x < i < i < i).

A seguir, apresentamos o algoritmo de proximidade k, conhecido como KNN.

Nós queremos fazer uma distribuição de dados de acordo com os dados x1, x2…xn do centro de treinamento (em que cada um deles é m-dimensional), sob a categoria ωi. Se x for um ponto arbitrário no espaço m-dimensional, como calcular P ((x + ωi)?

Sabemos que quando a quantidade de dados é grande o suficiente, é possível usar a probabilidade de aproximação proporcional. Utilizando este princípio, em torno do ponto x, encontre os k pontos de amostragem mais próximos do ponto x, dos quais quais pertencem à categoria i. Calcule o volume V da superesfera mínima em torno desse k ponto de amostragem; além disso, encontre o número de Ni que pertence à classe ωi em todos os dados da amostragem:

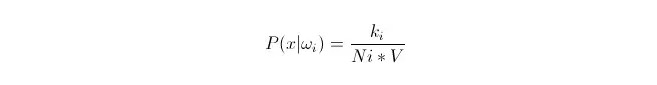
Como você pode ver, o que nós calculámos foi a densidade de probabilidade condicional de classe no ponto x.

P (ωi) é igual a: De acordo com o método acima, P ((ωi) = Ni/N 。 onde N é o número total de amostras。 E então, P (x) = k/N.*V), onde k é o número de todos os pontos de amostragem em torno deste super-esferário; N é o número total de amostras. Então P (ωi 11:3x) pode ser calculado:

P(ωi|x)=ki/k

Para explicar a equação acima, em um super-esfera de tamanho V, temos k amostras envolvidas, das quais há ki pertencentes à classe i. Assim, quais são as amostras mais envolvidas, e então podemos determinar a qual classe x deve pertencer. Este é o classificador projetado com o algoritmo de proximidade k.