Aplicações Python e Bayes

Com base no teorema de Bayes, um classificador simples pode ser obtido sob a premissa de que as variáveis são independentes umas das outras. Em termos mais simples, um classificador simples assume que uma característica de uma classificação não está relacionada com outras características dessa classificação. Por exemplo, se um fruto for redondo e redondo e tem cerca de 3 cm de diâmetro, ele pode ser uma maçã. Mesmo que essas características dependam uma da outra ou dependam da existência de outras características, um classificador simples ainda assume que essas características indicam independentemente que a fruta é uma maçã.

• Os modelos Bayesian simples são fáceis de construir e muito úteis para grandes conjuntos de dados. Embora simples, o desempenho dos modelos Bayesian simples vai além de métodos de classificação muito complexos.

  O teorema de Bayes fornece um método para calcular a probabilidade p {\displaystyle p} de p {\displaystyle p} x {\displaystyle p} e p {\displaystyle p} x {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p} c {\displaystyle p}

  

  Aqui,

  P (c) é a probabilidade posterior de uma classe (objetivo) com a condição de que a variável (propriedade) seja conhecida. P© é a probabilidade anterior da classe P {\displaystyle p} é a probabilidade, ou seja, a probabilidade, de uma variável previsível, sob a premissa de uma classe conhecida. P (x) é a probabilidade antecipada da variável de previsão. Exemplo: Vamos entender o conceito com um exemplo. Abaixo, eu tenho um conjunto de treinamento do clima e a variável de objetivo correspondente, Play Play. Agora, precisamos classificar os participantes que estão brincando e não brincando de acordo com as condições do tempo.

  Passo 1: Converte o conjunto de dados para uma tabela de frequências.

  Passo 2: Utilize uma probabilidade semelhante a 0,29 para criar uma tabela de probabilidade, quando a probabilidade de Overcast é de 0,64 para criar uma tabela de probabilidade.

  

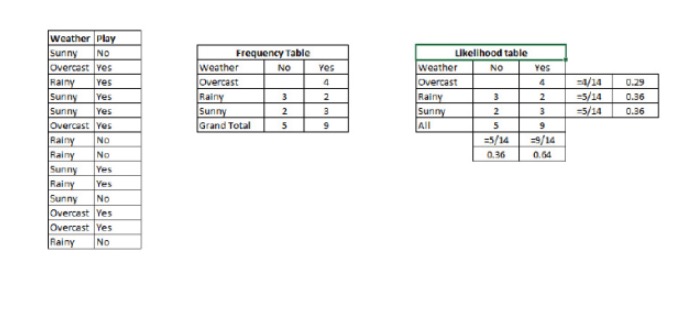
  Passo 3: Agora, calcule a probabilidade posterior de cada classe usando as equações de Bayes simples. A classe com maior probabilidade posterior é o resultado da previsão.

  Pergunta: Se o tempo estiver bom, os participantes podem brincar.

  Podemos resolver este problema usando o método que discutimos. Então, P (será divertido) = P (será divertido) * P (será divertido) / P (será divertido)

  Então temos P = 3/9 = 0.33, P = 5/14 = 0.36, P = 9/14 = 0.64.

  Agora, P (que vai jogar) é igual a 0,33 vezes 0,64 / 0,36 é igual a 0,60, com uma probabilidade maior.

  O simples Bayes usa um método semelhante para prever probabilidades de diferentes categorias através de diferentes propriedades. Este algoritmo é frequentemente usado para classificar textos, bem como para problemas que envolvem várias categorias.

• Código Python:

#Importar Biblioteca do sklearn.naive_bayes importar GaussianNB - Não. # Assumindo que você tem, X (predictor) e Y (alvo) para o conjunto de dados de treinamento e x_test(predictor) de test_dataset

Criar modelo de objeto de classificação SVM = GaussianNB()

há outra distribuição para classes multinomiais como Bernoulli Bayes ingênuo, link de referência

Treinar o modelo usando os conjuntos de treinamento e verificar a pontuação

model.fit(X, y) - Não. #Predizir o resultado previsão= modelo.predicção ((x_test)