Байесовский классификатор на основе алгоритма KNN

Теоретические основы для разработки классификатора для принятия классификационных решений Теория решений Бэйеса:

Сравнение P(ωi radux) ≠, гдеωi - класс i, x - данные, которые наблюдаются и должны быть классифицированы. P(ωi radux) означает, какова вероятность того, что данные относятся к классу i при наличии известных характеристических векторов данного данного данного, что также становится последующей вероятностью. В соответствии с формулой Бейеса, она может быть представлена как:

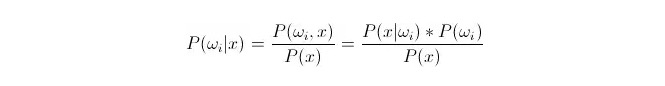
Из них, P ((x 1.13) i) называется вероятностью сходства или условной вероятностью; P ((ωi) называется вероятностью предшествия, поскольку она не связана с экспериментом и может быть известна до эксперимента.

При классификации, при заданном x, выбирается та категория, которая делает вероятность обратной проверки P ((ωiⴰⵙⴰⵙx) наибольшей. При сравнении каждой категории под P ((ωiⴰⵙx) величиной,ωi является переменной, а x - фиксированной; поэтому можно исключить P ((x) и не учитывать ее.

Итак, мы получим P (x) = P (x) = P (x) = P (x).*Вопрос P ((ωi)) Предварительная вероятность P ((ωi) может быть, если сосредоточить статистическую подготовку на пропорции данных, появляющихся в каждой классификации.

Вероятность P (x < i < i) является невыполнимой, поскольку x - это данные из тестового набора, которые не могут быть получены непосредственно из тренировочного набора. Тогда нам нужно найти закон распределения данных тренировочного набора, чтобы получить P (x < i < i < i).

Ниже представлен алгоритм k-близкого соседства (англ. KNN).

Мы хотим сопоставить распределение этих данных в классе ωi с данными x1, x2…xn из тренировочного центра (каждое из которых является m-мерным). Предположим, что x является любой точкой в m-мерном пространстве, как вычислить P (x) {\displaystyle P (x) } ?

Известно, что при достаточно большом количестве данных можно с помощью пропорционального приближения вероятности. Используя этот принцип, в окружности точки x, найдите наиболее близкие к пунктам выборки, относящиеся к категории i. Вычислите объем V наименьшей сверхсферы, окружающей эту k точку выборки; а также найдите число Ni, относящихся к категории ωi во всех данных выборки:

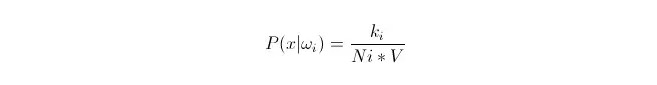
Как вы можете видеть, то, что мы вычислили, это, фактически, плотность условной вероятности класса в точке x.

P (ωi) - это что? Согласно вышеуказанному методу, P ((ωi) = Ni/N 。, где N - общее количество образцов。 Кроме того, P (x) = k/N.*V), где k - число всех пробных точек, окружающих этот сверхсфера; N - общее число проб. Если вы используете формулу, то вы можете легко вычислить:

P(ωi|x)=ki/k

Поясним вышесказанное: в суперсфере размером с V окружены k образцов, из которых i относится к классу ki. Таким образом, из наибольшего количества окруженных образцов мы можем определить, к какому классу здесь должен относиться x. Это классификатор, разработанный с помощью алгоритма k близкого соседства.