Python Простые приложения Bayes

При условии взаимной независимости предсказуемых переменных можно получить простую классификацию Бейеса согласно теории Бейеса. Проще говоря, простуя классификация Бейеса предполагает, что одно из свойств классификации не связано с другими свойствами этой классификации. Например, если плод круглый и красный, и его диаметр составляет около 3 дюймов, то это может быть яблоко. Даже если эти свойства зависят друг от друга или зависят от наличия других свойств, простуя классификация Бейеса предполагает, что эти свойства независимо указывают на то, что плод является яблоком.

• Простые модели Бейеса легко создаются и очень полезны для больших наборов данных. Простые, но простые модели Бейеса выходят за рамки очень сложных методов классификации.

  Теорема Байеса дает способ вычислить вероятность P (c) x из P©, P (x) и P (x) c.

  

  Здесь,

  P (c) x - это вероятность последнего действия класса (c) при условии, что известные предсказательные переменные (c) имеют свойства (c) P© - это предшествующая вероятность P (x) c - вероятность, то есть вероятность предсказания переменной при условии известного класса. P (x) - предварительная вероятность предсказуемой переменной Пример: Давайте рассмотрим пример для понимания этой концепции. Ниже у меня есть тренировочный набор погоды и соответствующая целевая переменная Play Play. Теперь мы должны классифицировать участников, которые будут играть и не играть в соответствии с погодой. Давайте выполним следующие шаги.

  Шаг 1: Преобразуйте набор данных в таблицу частот.

  Шаг 2: Используйте аналогичную таблицу вероятности, когда вероятность Оверкаста составляет 0.29 и вероятность игры составляет 0.64, чтобы создать таблицу вероятности.

  

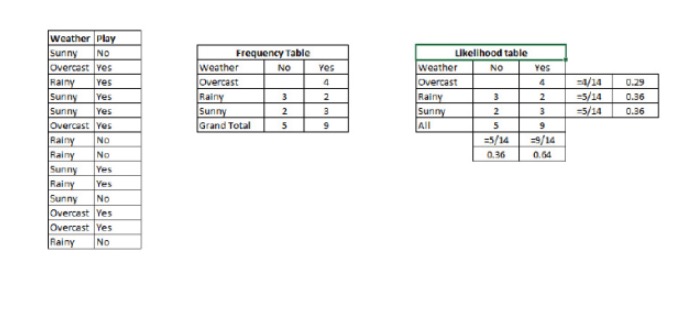
  Шаг 3: Теперь, используя простые уравнения Байеса, вычислите вероятность последствий каждого класса. Класс с наибольшей вероятностью последствий является результатом прогноза.

  Вопрос: Если будет хорошая погода, участники смогут поиграть.

  Мы можем решить эту задачу, используя методы, которые мы обсуждали ранее.

  У нас есть P, что равно 3/9 = 0.33, P, что равно 5/14 = 0.36, P, что равно 9/14 = 0.64.

  Теперь, P (все будет хорошо) = 0.33 умножить на 0.64 / 0.36 = 0.60, есть большая вероятность.

  Простуй Байес использует аналогичный метод, чтобы предсказать вероятность различных категорий с помощью различных свойств. Алгоритм обычно используется для классификации текста, а также для задач, связанных с несколькими категориями.

• Код Python:

#Import Библиотека Из sklearn.naive_bayes импорт GaussianNB - Я знаю. # Предположим, что у вас есть, X (предсказатель) и Y (цель) для набора данных обучения и x_test ((предсказатель) набора данных test_data)

Создать модель объекта классификации SVM = GaussianNB()

существует другое распределение для многочленных классов, таких как Бернулли Наивный Байес, Ссылка ссылка

Обучение модели с использованием наборов обучения и проверка баллов

model.fit(X, y) #Предскажите результат предсказанное= model.predict ((x_test)