Python đơn giản Bayes ứng dụng

Theo định lý Bayes, một cách phân loại đơn giản Bayes có thể được thực hiện nếu các biến số được dự đoán là độc lập với nhau. Nói một cách đơn giản hơn, một phân loại đơn giản Bayes giả định rằng một thuộc tính của một phân loại không liên quan đến các thuộc tính khác của phân loại đó. Ví dụ, nếu một trái cây tròn và đỏ, và có đường kính khoảng 3 inch, thì trái cây có thể là quả táo.

• Mô hình Bayes đơn giản dễ xây dựng và rất hữu ích cho các bộ dữ liệu lớn. Mặc dù đơn giản, nhưng biểu hiện của Bayes đơn giản vượt ra ngoài các phương pháp phân loại rất phức tạp.

  Định lý Bayes cung cấp một phương pháp tính toán xác suất sau thử nghiệm P (c) từ P©, P (x) và P (x) c. Xem phương trình sau:

  

  Ở đây,

  P (c) là xác suất hậu quả của một mục tiêu của một lớp (c) với một giả định về một tính năng được biết. P© là xác suất trước của lớp P (x) c là khả năng, nghĩa là xác suất của một biến thể được dự đoán với một giả định về một loại được biết. P (x) là xác suất trước của một biến Ví dụ: Để hiểu khái niệm này bằng một ví dụ. Dưới đây, tôi có một tập huấn về thời tiết và các biến mục tiêu tương ứng là Play Play. Bây giờ, chúng ta cần phân loại những người tham gia cuộc họp chơi và không chơi dựa trên tình hình thời tiết.

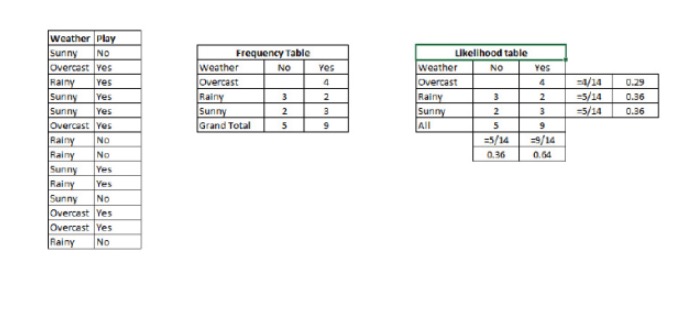
  Bước 1: Chuyển bộ dữ liệu thành bảng tần số.

  Bước 2: Tạo bảng likelihood bằng cách sử dụng likelihood khi Overcast có khả năng là 0.29 và game có khả năng là 0.64

  

  Bước 3: Bây giờ, sử dụng các phương trình Bayes đơn giản để tính toán xác suất hậu quả của mỗi lớp; lớp có xác suất hậu quả lớn nhất là kết quả của dự đoán.

  Câu hỏi: Nếu thời tiết đẹp, người tham gia có thể chơi.

  Chúng ta có thể giải quyết vấn đề này bằng cách sử dụng phương pháp mà chúng ta đã thảo luận.

  Chúng ta có P = 3/9 = 0.33, P = 5/14 = 0.36, P = 9/14 = 0.64.

  Bây giờ, p (được chơi) = 0.33 x 0.64 / 0.36 = 0.60, có khả năng cao hơn.

  Bayes đơn sơ sử dụng một phương pháp tương tự để dự đoán các loại xác suất khác nhau thông qua các thuộc tính khác nhau.

• Mã Python:

#Buy nhập Thư viện từ sklearn.naive_bayes import GaussianNB # Giả sử bạn có, X (nghiên đoán) và Y (mục tiêu) cho tập dữ liệu đào tạo và x_test ((nghiên đoán) của test_dataset

Tạo mô hình đối tượng phân loại SVM = GaussianNB()

có phân bố khác cho các lớp đa số như Bernoulli Bayes ngây thơ, liên kết tham chiếu

Đào tạo mô hình bằng cách sử dụng các bộ đào tạo và kiểm tra điểm số

model.fit(X, y) # Dự đoán sản lượng dự đoán= model.predict ((x_test)