Das unsichtbare Markovmodell

Das unsichtbare Markovmodell

• Erstens: Erkennen

  Heute wollen wir Ihnen eine einfache Anwendung des HMM (Markov-Modell) auf Aktien zeigen.

  Das versteckte Markov-Modell, das auf den ersten Blick hochwertig klingt und keinerlei Ahnung hat, was es ist, dann lassen Sie uns einen Schritt zurückgehen und zuerst Malkov-Ketten betrachten.

  Die Markov-Kette, benannt nach Andrej Markov (A.A. Markov, 1856-1922), ist ein Zufallsprozess in Mathematik mit Markovischen Eigenschaften. Bei gegebener aktueller Erkenntnis oder Information ist die Vergangenheit (d. h. der aktuelle historische Zustand) unabhängig von der Vorhersage der Zukunft (d. h. der Zustand der Zukunft nach der Gegenwart).

  

  In diesem Prozess hängt die Verlagerung jedes Zustands nur von den n vorhergehenden Zuständen ab. Dieser Prozess wird als ein n-stadial Modell bezeichnet, in dem n die Anzahl der veränderten Zustände beeinflusst.

• Zweites Beispiel:

  Die mathematische Ausdrucksweise sieht wie folgt aus:

  

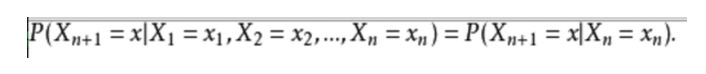
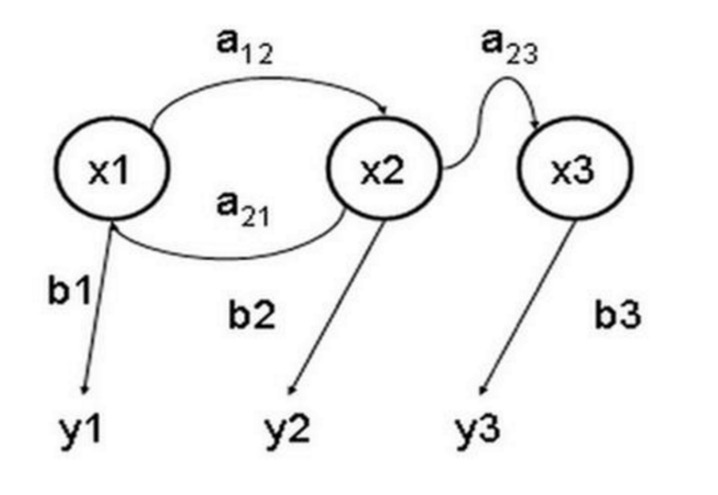
  Nehmen wir ein Beispiel aus unserem Alltag, in dem wir versuchen, das zukünftige Wetter auf der Grundlage der gegenwärtigen Wetterlage vorherzusagen. Ein Weg ist die Annahme, dass jeder Zustand in diesem Modell nur von dem vorhergehenden abhängt, nämlich die Markov-Annahme, die das Problem enorm vereinfacht. Natürlich ist dieses Beispiel auch etwas unrealistisch.

  

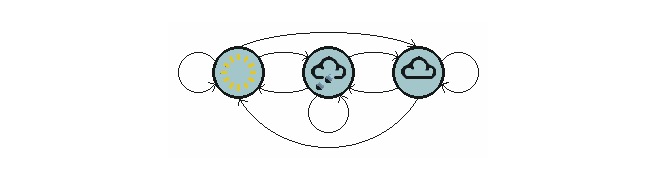
  Die obige Abbildung zeigt ein Modell, in dem die Wetterverschiebung stattfindet.

  Beachten Sie, dass ein Stufenprozess mit N Zuständen N2 Zustandswechsel aufweist. Die Wahrscheinlichkeit für jeden Wechsel ist die Zustandswechselwahrscheinlichkeit, also die Wahrscheinlichkeit, dass er von einem Zustand in einen anderen wechselt. Alle diese N2 Wahrscheinlichkeiten können mit einer Zustandswechselmatrix dargestellt werden, die in dem oben genannten Wetterbeispiel wie folgt dargestellt wird:

  

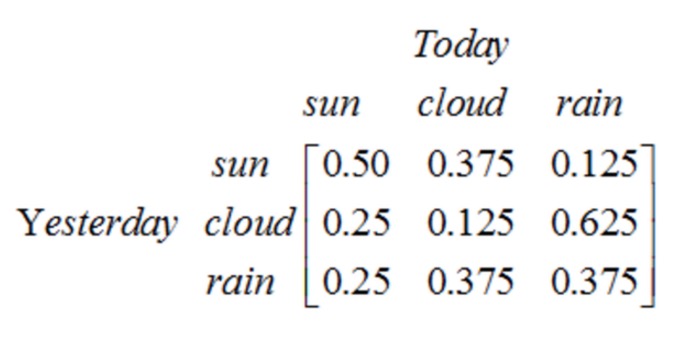
  Diese Matrix sagt, dass es 25% Chancen gibt, dass es heutzutage klar ist, 12,5% Chancen auf Nebel und 62,5% Chancen auf Regen, wenn es gestern blau war.

  Um ein solches System zu initialisieren, benötigen wir einen anfänglichen Wahrscheinlichkeitsvektor:

  

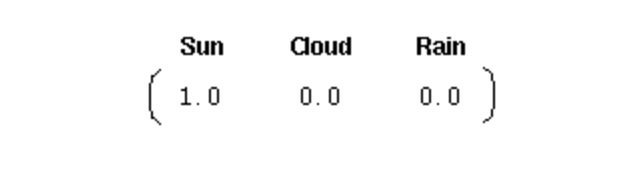
  Dieser Vektor zeigt, dass der erste Tag schön ist. Hier definieren wir die folgenden drei Teile für den Markov-Prozess der ersten Stufe:

  Der Zustand: Sonnenschein, Nebel und Regen.

  Initial Vector: Definition der Wahrscheinlichkeit des Zustands des Systems, wenn die Zeit 0 ist.

  Zustandsverschiebungsmatrix: Die Wahrscheinlichkeit jeder Wetterumwandlung. Alle Systeme, die so beschrieben werden können, sind ein Markov-Prozess.

  Was tun wir jedoch, wenn Markov-Prozesse nicht stark genug sind? In einigen Fällen sind Markov-Prozesse nicht genug, um die Muster zu beschreiben, die wir hoffen zu finden.

  Wenn wir beispielsweise den Markt beobachten, können wir nur die Preise und den Handel an diesem Tag kennen, aber nicht wissen, in welchem Zustand der aktuelle Markt ist (Bull, Bear, Shock, Rebound usw.), in diesem Fall haben wir zwei Zustandsmengen, eine beobachtbare Zustandsmenge und eine versteckte Zustandsmenge (Stock-Stand). Wir möchten einen Algorithmus finden, der die Zustände der Aktien auf der Grundlage der Zustände der Aktienpreise und der Markov-Hypothese prognostizieren kann.

  In diesen Fällen sind die beobachtbaren und versteckten Zustandssequenzen wahrscheinlichkeitsbezogen. Wir können also Prozesse dieser Art modellieren, die einen versteckten Markov-Prozess und eine beobachtbare Zustandssammlung, die mit der Wahrscheinlichkeit dieses versteckten Markov-Prozesses verknüpft ist, ein verstecktes Markov-Modell darstellen.

  Das versteckte Markov-Modell ist ein statistisches Modell, das verwendet wird, um einen Markov-Prozess mit impliziten unbekannten Parametern zu beschreiben. Die Schwierigkeit besteht darin, die impliziten Parameter des Prozesses aus den beobachtbaren Parametern zu ermitteln und diese Parameter dann für eine weitere Analyse zu nutzen.

  

  Veranschaulichen wir dies mit dem Beispiel einer Würfel: Nehmen wir an, ich habe drei verschiedene Würfel in meiner Hand. Die erste Würfel ist unsere gewöhnliche Würfel (wir nennen sie D6), mit sechs Seiten, wobei die Wahrscheinlichkeit, dass jede Seite erscheint, 1/6 ist. Die zweite Würfel ist eine Vierecke (wir nennen sie D4), wobei die Wahrscheinlichkeit, dass jede Seite erscheint, 1/4 ist. Die dritte Würfel hat acht Seiten (wir nennen sie D8), wobei die Wahrscheinlichkeit, dass jede Seite erscheint, 1/8 ist.

  

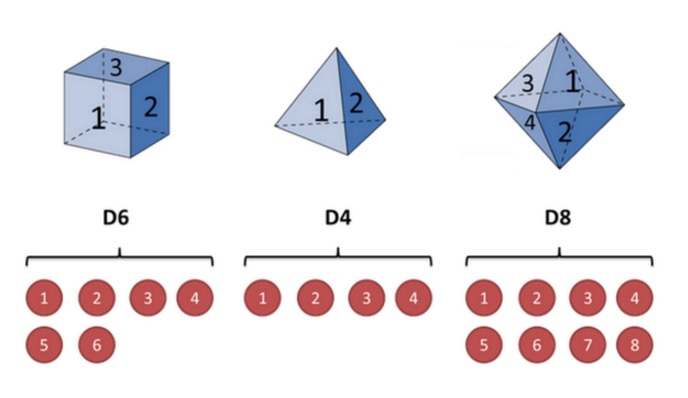
  Nehmen wir an, wir beginnen mit einer Würfel, wir wählen eine von drei Würfeln, und die Wahrscheinlichkeit, dass jede Würfel ausgesucht wird, beträgt 1/3. Dann wählen wir eine Würfel, und wir erhalten eine Zahl, eine von 1, 2, 3, 4, 5, 6, 7, 8.

  Diese Zahlenreihe wird als sichtbare Zustandskette bezeichnet. In der Markov-Modellreihe haben wir jedoch nicht nur eine sichtbare Zustandskette, sondern auch eine implizite Zustandskette. In diesem Fall ist die implizite Zustandskette die Folge der Käse, die Sie verwenden.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  Ebenso gibt es eine Wahrscheinlichkeit, die als Ausgangswahrscheinlichkeit bezeichnet wird, obwohl es keine Umwandlungswahrscheinlichkeit zwischen sichtbaren und impliziten Zuständen gibt. In unserem Beispiel ist die Ausgangswahrscheinlichkeit von 1, wenn ein Sechseck (D6) 1 erzeugt, 1/6. Die Ausgangswahrscheinlichkeit von 2, 3, 4, 5, 6 ist ebenfalls 1/6. Wir können auch eine andere Definition der Ausgangswahrscheinlichkeit machen.

  

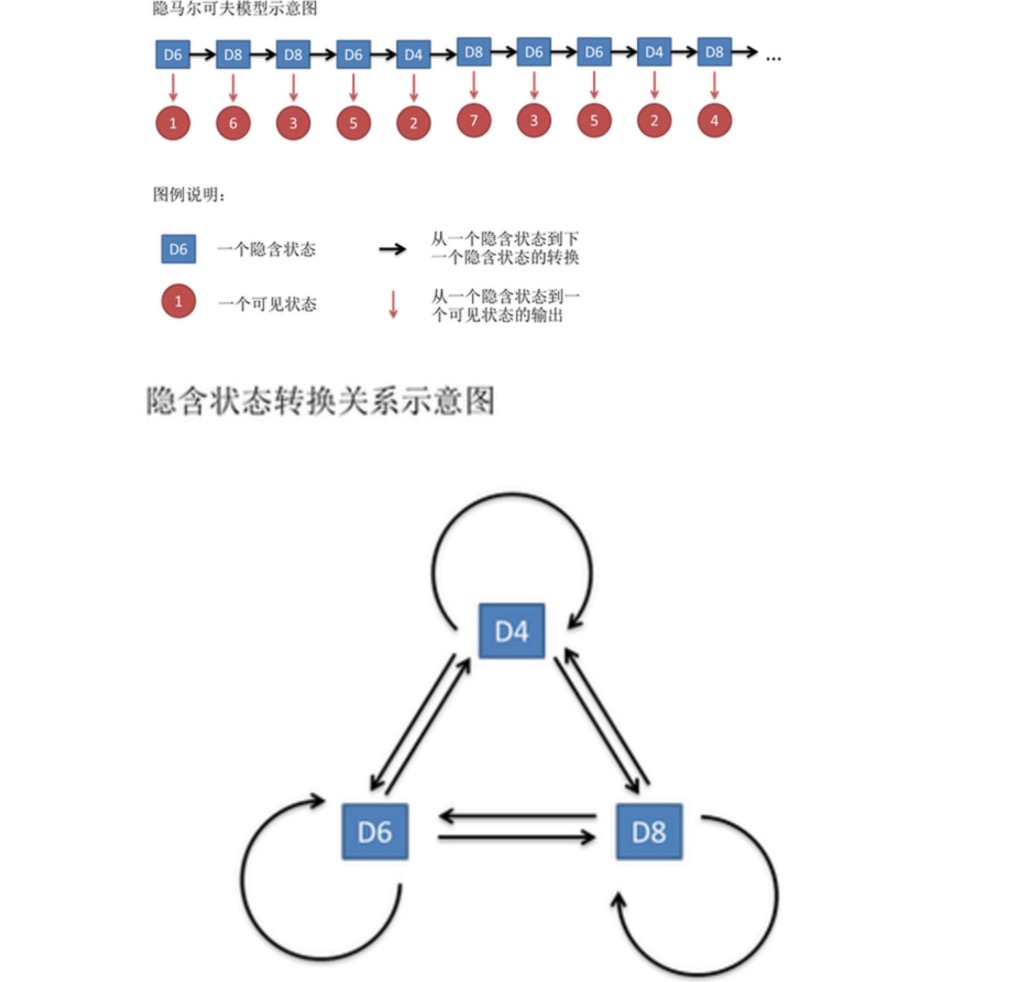
  Für HMM ist es relativ einfach, wenn man im Voraus die Conversion-Wahrscheinlichkeit zwischen allen impliziten und den Ausgabe-Wahrscheinlichkeiten zwischen allen impliziten und allen sichtbaren Zuständen kennt. Aber bei der Anwendung des HMM-Modells fehlt oft ein Teil der Information. Manchmal weiß man, dass es mehrere Kästchen gibt, was jede Käse ist, aber weiß nicht, welche Kästchen-Sequenz herausgekommen ist.

  Die Algorithmen, die mit HMM-Modellen in Verbindung stehen, sind in drei Kategorien unterteilt und lösen jeweils drei Probleme:

  • Wenn ich weiß, dass es mehrere Arten von Monkeys gibt (die Anzahl der impliziten Zustände), was jede Arten von Monkeys sind (die Umwandlungswahrscheinlichkeit), und je nach Ergebnis der Monkeys (die sichtbaren Zustandsketten), möchte ich wissen, welche Arten von Monkeys (die impliziten Zustandsketten) jedes Mal herauskommen.

  • Ich weiß auch, dass es mehrere Monkeys gibt (die Anzahl der impliziten Zustände), was jede Monkeys ist (die Umwandlungswahrscheinlichkeit), und ich möchte wissen, welche Wahrscheinlichkeit es gibt, dass diese Monkeys aus dem Ergebnis (die sichtbare Zustandskette) herauskommen.

  • Wenn ich weiß, dass es mehrere Monkeys gibt (die Anzahl der impliziten Zustände), wenn ich nicht weiß, was jede Monkey ist (die Umwandlungswahrscheinlichkeit), wenn ich die Ergebnisse vieler Monkeys beobachte (die sichtbaren Zustandsketten), möchte ich umkehren, was jede Monkey ist (die Umwandlungswahrscheinlichkeit).

    Wenn wir die Probleme der Börse lösen wollen, müssen wir die Probleme 1 und 3 lösen. In einem nächsten Artikel werden wir sehen, wie das gelingt.

Übertragen von: