Metcalfe's law in Bitcoin

Cryptocurrencies are a new asset class, and researchers are just beginning to better understand the fundamental forces behind their price movements. A new research paper suggests that the price of Bitcoin can be modeled using Metcalfe's law. This property of Bitcoin and other cryptocurrencies is very similar to Facebook, in that their value depends on the number of active users and the size of the network.

This is a summary:

We show by example that the long-term price of Bitcoin is non-random and can be modeled as a function of the number of users n growing over time. Using observed Facebook and Bitcoin data, we infer the relationship between price, number of users and time, and show that the resulting market value may obey the Gompertz sigmoid growth function. This function, which has historically been used to describe the growth of organisms such as bacteria, tumors and viruses, may have some applications in network economics.

The following is a noteworthy quote from an academic research paper:

This paper provides a simple explanation of price formation in the emerging and often misunderstood cryptocurrency ecosystem. With Bitcoin as an example, we provide compelling empirical evidence that price formation is not a semi-random result of emotional investment, but is based on a recently recognized value economy principle: cyber economics.

An examination of the price of Bitcoin provides some interesting observations that directly refute the myth that the value of a coin is a myth. First, as its proponents have long argued, the value of a currency is largely dependent on its use and acceptance. This hypothesis has been verified, and it is also clear from a close examination that the relationship between the price of Bitcoin and the activity associated with the Bitcoin payment network is strong.

Metcalfe's law is based on a mathematical equation describing a connection between n users. Thus, the network value V is a function of the number of users n. The mathematical basis of Metcalfe's law is based on a pairwise connection (e.g., a telephone). If there are four people on a network using a telephone, there may be a total of 3 + 2 + 1 = 6 connections.

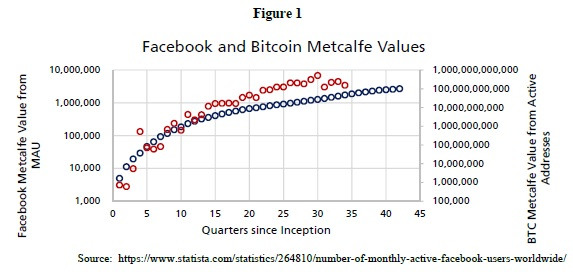
Facebook is well-suited for comparison with Bitcoin. The length of each data series is almost the same (about 10 years). Both are quite innovative, although not entirely original (Digicash ahead of Bitcoin, MySpace ahead of Facebook). It is rare to see a currency (or other asset) gradually adopted over time. This is partly because many companies are privately owned in their developmental stages.

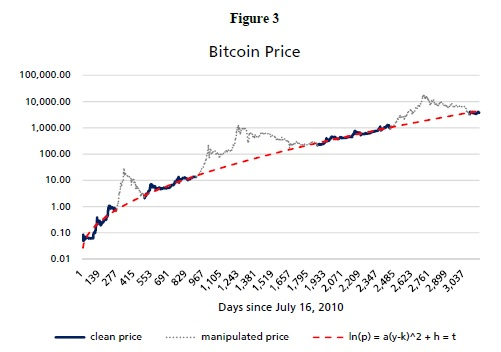
Looking back at Figure 3, there are three notable exceptions, Bitcoin's price deviates from parallelized trends. These are periods of recorded price manipulation and eventual equilibrium. These peaks represent price deviations that cannot be explained by user-related factors. User-related factors are driven by user growth or network usage. These factors include transactions, active accounts, wallets, nodes, and hash rates. These factors are highly correlated with each other, and the effects of these factors' changes are reflected in the Metcalfe value.

If n grows at a constant rate, then log ((n) is linear. Since we observed that log ((n) is non-linear in Facebook and Bitcoin (Fig. 7), n grows at a non-constant rate, indicating adoption at different stages. This cumulative growth rate pattern produces an S-shaped function (Gompertz function) that has been used for decades to simulate viral infection, bacterial growth, tumor growth, and mobile phone proliferation.

The original link:https://quantpedia.com/metcalfes-law-in-bitcoin/