The story of the escape and the survival of the gambler and the gambler
Author: Inventors quantify - small dreams, Created: 2016-12-26 11:47:56, Updated:The story of the escape and the survival of the gambler and the gambler
** When it comes to gambling and investing, people are usually in a hurry to learn the tricks of making money, in fact, I think that making money is not easy to learn, it requires experience and insight. I'm ready to write a series of books about escapism, not to teach my kids about escapism, but to discuss the lessons of escapism with my colleagues and colleagues. Inspired by an interview I did with the Red Week of the Wall Street Journal three years ago. At the urging of a reporter, I gave a detailed insight into the investment banking business, a broad outline of the financial situation in the world economy, and some trading tips. I thought I would present myself to the readers as a high-flying, visionary expert, and two days later the draft came out:
-
Wall Street manipulator Fish Yang's secret escape from his life
I'm a bit of a teapot.
In the interview, he only spoke about the importance of risk control, cited several examples of successful breakthroughs in his own transactions, how did he become a hedge fund manager? However, after thinking about it carefully, I had to admire the sharpness of the journalist's editor. The US investment bank is a little far from the Chinese people, and the ambition of the big situation is no less than me, hedge fund management is a relatively empty topic.
The master of martial arts, who started with a mystery about Lord Kok, started a mystery about the way of Holmes, and he said that he might also start with a mystery about escaping from life and develop a mystery about escaping from life.
I'll say hello first: I'm a little distracted, and if you're away, I'll see you guys.
Recently, it has been found that the most interesting part of many readers about the chaotic world of Wall Street gambling is the opening section about gambling (before that, a London trader had sent an e-book to a friend who had left a mailbox in the hope that it would be helpful to everyone). It seems that 21 is closer to the masses after all than the interest rate expires. In fact, gambling and investing are very similar, and the experience in the casino is also very helpful to me as a trader on Wall Street.
-
Living is the most important thing.
When it comes to gambling and investing, people are usually in a hurry to learn the tricks of making money, in fact, I personally think that the way to make money is not easy to learn, and requires a lot of experience and insight. Beginners should quickly improve their level of skill, but should focus on practicing defense first.
In short, there is absolutely no sacrifice before the victory of the revolution. Don't think it's easy, and let's not forget that there are a lot of people around us who are trying to get rich, even if they are among the very best in the investment world.
Here are a few examples:
Jesse Livermore: A Stockbroker's Memoir is a memoir about Jesse Livermore, a genius in the speculative world who started out with nothing and became a $100 million dollar man in 1929, eventually filing for bankruptcy and committing suicide a few years later.
John Merriweather: Formerly a super trader at King's Bench, Solomon Brothers, and later the founder of the LTCM group of long-term capital hedge funds, which once had a massive $4 billion in capital but almost lost it all in the 1998 Russian bond crisis.
He founded All Nations Securities in 1988 and was known as the father of Chinese securities, but in 1995 he lost his lead in the 3.27 state-debt scandal.
Dong Wan Xin: The former head of the DeLung family of enterprises, who was arrogant about the Chinese capital market, ended up collapsing due to the collapse of the DeLung empire when the capital chain was broken.
All of the above, who are considered geniuses of the capital market, failed in the end. Their experience tells us that if they do not take care of the risk control, the scene in the fisherman and the goldfish trap will happen: the effort to fight is the pope, and the result is a log cabin by the sea.
It's important to be alive.
-
No way to know. No way to know.
Many years ago, I used to take a bus from New York's Chinatown to Atlantic City, mostly with working people who worked in the lobby of restaurants. Most of them were trying to change their fortunes in casinos, but often with meager salaries. I remember one time, a girl next door said that she went to the casino every week to play ballet and had a set of winning secrets.
When I was on my way back, I won $800 and she lost $4,000. I was surprised to see that $4,000 should have been her monthly income! Seeing my compatriot in a car full of simple clothes, I suddenly felt very sad and hated those who are in the business of making money on the bus, just like sending a sheep to the tiger's mouth! I tried to tell the girl who plays the ballet that she will lose for a long time, but she refused to believe, saying that this time it was just bad luck, next week to repeat the book.
I'm speechless, too many failures are used as an excuse to get lucky.
A win and a loss is indeed luck, and a win and a loss of 10,000 is the majority theorem. Is it not a matter of time before the gamblers in the casino repeatedly bet on the game with the advantage of the odds? So there is a saying: The casino is not afraid of you winning, afraid of you not coming.
The same goes for investing.
The stock market is better than the casino, and in the long run it should be a positive return game. But due to factors such as making a house, insider trading, stamp duty, it is difficult for ordinary investors to win the big market if they cheat too frequently, and the return rate is difficult to win, and even may lose. So, do not believe the so-called trick of getting rich quick on the market, 99% is floating, 99% is negligent.
In the Edo period of Japan, there was a swordsman, Saint Seiya, who fought over sixty duels with humans, without ever losing. He was not only skilled, but also had a secret: he never fought with people stronger than himself.
I'm not sure, I'm not sure.
This is the first thing hackers and investors need to remember.

-
What are the advantages of casinos?
Casinos are not afraid of you winning, they are afraid that you won't come, because casino games are basically a game of chance and chance. Many players are superstitious about luck and chance, while those who run casinos believe in probability, which is the difference between losers and winners.
For example, in roulette (see figure below), a player can bet on any number, and the casino wins 35 times if the small ball on the turntable lands on that number.
It sounds tempting, doesn't it?
The young man in the film Casablanca, who escaped from Europe, was arrested 22 times and paid for his trip to the United States.
Let's take a quick look at it.

If there are only 1-36 of these 36 numbers, then the player wins 1 dollar per bet, on average every 36 spins, and the 35 dollars won exactly offset the other 35 losses. But the casino adds a 0 on the left side of the wheel, the player's winning face becomes 1/37, the 35 won is not enough to offset the other 36 losses, the casino occupies a probability advantage of 1/37 = 2.70%, that is, the player will lose an average of 2.7 dollars per 100 bets.
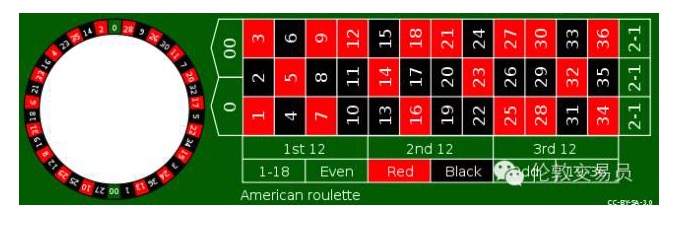
In addition to single-number bets, there are also other games such as red and black bets. Whether it is a single-number bet of 1 to 35 or a red and black bet of 1 to 1, the winning side of the casino is the same. But there is still an important difference between the two: the losing and winning fluctuations of single-number bets are clearly greater than those of red and black bets.
First of all, let's say that the payoff and volatility are two of the most crucial aspects of gambling and investing.
It is best not to play the game, but to play, you should choose to lose and win with high volatility; investment should be chosen with low volatility.
Back to gambling, most casino games are designed similarly to roulette: casinos have a probability advantage. In these games, players can win money if they play only a few hands, and if they are lucky, they can almost certainly lose money in the long run. This is called the Law of Large Numbers theorem in mathematics.
However, the casino's organs are exhausted, and mathematicians have found a loophole.
-
21 years old story
In the early 1960s, an American mathematician named Edward Thorp, using the newly emerged computer, found an opportunity in the 21-point game to develop a method to beat the casino by card counting. Professor Thorp put the theory into practice, connected the jackpot casinos with his own card counting method, and was quickly blacklisted, so someone wrote a book about it!
"Beat the Dealer" sold over 700,000 copies and topped the New York Times bestseller list (reminiscent of the equally brilliant "Wall Street Gang", which the author was ashamed of...) and the royalties far outweighed Gamble's earnings.
Soup's card counting method is not difficult. The rules of the 21-point rule: the player and the dealer (the casino) face each other to see which hand is closer to the sum of their cards (but not more than) 21 points. 10, J, Q, and K are all ten points.
At the beginning of the game, the player and the dealer are dealt two cards each, and the dealer's cards are dealt face down. Then the player makes a decision: can he grab a card, do special actions such as doubling, or at any time choose to fold. If the player exceeds 21 points, the player immediately loses.
In addition, there is a special rule: an A and a ten-point card (*10, J, Q, K) called a blackjack, the holder wins directly. If the player gets a blackjack, he can win 1.5 times the chip. If the dealer gets a blackjack, he can only win 1 times the chip.
It is clear that the house and the player have an advantage in the 21-point game. The house advantage is that the player can win if the player is the first to open the hand. The player's advantage is the flexibility of the player's movements and the ability to decide on tactics based on their own cards and the cards exposed by the house.
The more ten and A cards, the more likely it is that a blackjack will appear, and the more likely it is that the player will be able to make a flip, and the more valuable the advantage of the player's maneuverability. Conversely, the more small cards, such as 3, 4, 5, 6, and so on, the less likely it is that the flip will occur, which is in the dealer's favor.
21 points more than in the Soup era with 1 or 2 pairs of poker cards, when the cards are just washed, the casino occupies a probability advantage of about 0.5%. The trick is that, as the draw proceeds, at times the ratio of big cards and A will be higher, and the probability will turn in favor of the player. The method of Soup winning the casino is: by counting the probability, make a big bet when the situation is favorable!
The first generation of the Sotheby's chain invented the card game, wrote a best-selling book, and then got rich on Wall Street, and later made a fortune in hedge funds.
As for the casino side, a group of card counters that have mastered So-seok's power have since emerged. The casino side tried their best to turn the card counters away, while the card counters dug their way through the blockade.
(Please rest assured, the story will eventually return to investment..)
-
The MIT team
Speaking of soup, the casino has more trouble with a card counting dealer. Over time, the casino side gradually accumulates a blacklist. If the person on the list is recognized at the 21 point card table, they are usually immediately greeted with a gift: You can go play somewhere else!
During the height of the card-counting scandal in the 1980s, a detective hired by the casino put together a list of blacklists and discovered an important clue: many card counters were located near Cambridge, Massachusetts! Cambridge, Massachusetts You may not have heard of it, but the two universities located here you can not have not heard of: Harvard and MIT.
But then the truth came out, and there was a group of MIT students playing cards!
This is a business-as-usual organization: some people make money, some people manage, some people join the ranks, the whole of the hedge fund model of hedge fund investing and hedge risk control. The biggest advantage of team hedge funds is that the risk faced by individual hackers can be avoided: 21 points of win-loss volatility is high, depending on your skill level, and in the short term, bad luck may also transfer light money, group operations can spread this risk.
For example, Michael is in charge of counting cards, and every time he makes a small bet, he throws out a pre-agreed code when the situation is favorable, and when he pretends to be James, he comes over and makes a bet of $1,000.
The MIT group operated for more than a decade, and schools such as MIT and Harvard were involved, including Chinese who had won gold medals in the Olympics. The soldiers who fought in the battle of the bulge, after all, were the most important mathematical genius in Cambridge, Massachusetts. The group's profits were said to be in the millions of dollars.
By the mid-1990s, as the U.S. economy was booming and gang members were moving to Silicon Valley, Wall Street, and elsewhere, the MIT accounting group was slowly disappearing. This also seemed to prove the point: young people doing the right thing would lead to a significant drop in crime rates.
A few years later, a fellow student from China, Pesky Yang, came into contact with the 21 point counting system and was very interested. I had never heard of Sope and did not know that the book sold for only a dozen bucks, and I spent $100 to buy the so-called "secret knife" from a negligent man named Kadosa. Although the knife was sold at a high price, I had a knife, after all, I also went to the casino to dig gold!
But the lake at that time was not the same lake that it was in that year.
-
Confusion about betting
After learning how to count cards, I was excited to go to Las Vegas for a little trial bull knife. The result was very good, I won a thick stack of 100 bucks, 21 points is a gold mine! I live in New York, it is impossible to always go to Las Vegas to mine gold, because there is also the second largest city in the United States, Atlantic City, so I became a regular there.
After a while, I began to realize that Atlantic City's gold-plated sands were not very good, that I generally won little and that the odds of winning and losing were very volatile. It was only after I studied it carefully that I realized that Atlantic City was not like Las Vegas.
As mentioned earlier, card counters mainly look at the proportion of big cards in the remaining cards, and when the proportion of big cards is higher than normal, they place a big bet.
Obviously, the ratio is most likely to be higher in two cases, the first is when there are few remaining cards, the second is when the 21-point game uses only 1-2 decks. The 21-point deadlock in the soap era has exactly these two characteristics: with only 1-2 decks, and the dealer will wash the cards almost with light, so the big card ratio is often higher, and the dealer has many opportunities to bet big when the situation is favorable.
Naturally, there are also high-level planners in the casino, who understand that the best soft defense against the counting card is to try to control the volatility of the ratio of the big and small cards, so the casino makes two poison counters. The first is to increase the number of 21 cards, from 1-2 pairs to 6-8 pairs.
It's obvious that a large number of cards and a small number of cards are not easy to change.
The second is to clear the cards early, avoiding the situation in which the ratio is most easily volatile. Las Vegas casinos are many, the competition is fierce, the casino also reserves some 21 points of 1-2 double cards for the gambler, I win mainly in those jackpots. And the Atlantic City geographical location is very strong, the gamblers from New York, Washington, and Philadelphia three densely populated areas run there, the casino does not care about business, so the rules of the 21 point game are especially tough for blackjack: basically there are 8 cards, and the washing is very diligent.
I was born in a small village in the south of the country, and I was born in a small village in the south of the country.
However, I still have a winning side to the casino when the odds are higher. The law of the majority: as long as there is a winning side, theoretically I will always play or win in the end. But in theory, there is an important constraint in practice: I have a limited amount of money, and I can't play. The majority law is just that the revolution will eventually win, but there is no guarantee that you will not sacrifice before the revolution wins.
Let's say I only have $10,000 and it's not easy to wait until I have a 1% probability advantage over the casino, and the dealer says:
Place your bets. (Please place bets..) How much am I betting? $20? Average win is $2, no problem.
If I catch a less black swan (which I lose 5 times), I lose the light. It seems that $20 is too little, $2,000 is too much, and the best bet should be between the two.
A tall man has already given an answer.
(I'm going to talk about investment theory.)
-
The Kelly formula
Last time I mentioned, it takes skill to bet when the situation is favorable. Too little betting is a wasted opportunity, too much betting increases the risk of losing the bet. What are some of the most appropriate bets?
f* is equal to (bp - q) /b where f* = the percentage of the total amount of the bet. p = probability of winning Q = probability of failure, q = 1-p b = odds, for example, betting on a single number in a roulette wheel, b = 35, betting on red and black, b = 1;
The 21 point betting problem mentioned above, assuming a total stake of $10,000, a player's probability of winning is 51%, odds are 1:1 (actual odds and odds are slightly off, but not too far apart), then the best bet given by Kelly's formula is:
So if we multiply this by 1 times 0.51 minus 0.49, over 1 is equal to $200. I know that many people see mathematical formulas as big heads, but you can't gamble and invest without using mathematics. The most important thing is not to calculate the numbers with the formula, but to understand the real meaning behind the formula.
First, the molecule bp - q in the formula represents the win-win situation, which in mathematics is called the expectation situation, and the Kelly formula states that the game with the expected value is the one that can be bet on, which is the most basic truth of all pranks and investments, that is, the previously mentioned gamble has no grasp, never bet.
Secondly, the odds of winning are also divided by the betting amount. That is, the smaller the odds are, the more you can bet. This is not easy to understand intuitively, we will illustrate with an example.
Liu Xiaobo: 20% chance of winning, 1 loss, 5 losses, all the way.20% to 80% is 20%. Bet: 60% chance of winning, 1 loss 1、bp - q = 160% - 40% is equal to 20%. The winning percentage is 80%, and the loser is 0.5。bp - q = 0.5*80% - 20% = 20%.
The mathematical expectation value of the three games is the same, all 20%, or say the average win of 100 yuan is 20 yuan. According to the tenacity of most Americans, I'm afraid I'll choose the game of bingo, right? But with the exception of the bingo in Kelly's formula, bingo can only bet 4% of the total amount, bingo can bet 20%, bingo can bet 40%.
In reality, most of the people who love to play games are hackers.
Who likes to play Big Brother? The casino!
Many professional investors on Wall Street also play the game of blackjack because of the convenience of leverage.
Finally, Kelly's formula indicates the importance of risk control: even a game with a positive expected value should not be over-bet. Mathematically, the percentage of money wagered exceeds Kelly's value, and the long-term rate of profit decreases, which greatly increases the likelihood of catastrophic losses.
Why is it that the investment community is losing out to some local tech-savvy old-timers? Most of the reason is that they are betting too big.
Liverpool lose to Maiden City
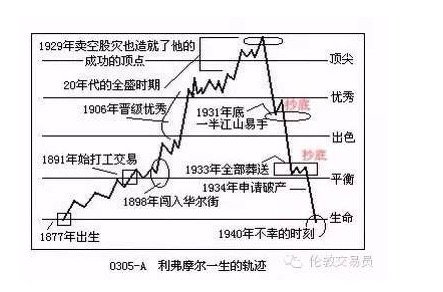
On November 28, 1940, 16 years before the Kelly formula was born, a former Wall Street recluse pulled out a pistol in the dressing room of the Waldorf Hotel in New York City and left a note for his wife: "Oh... I'm tired of fighting... this is the only release".
Jesse Livermore, the immortal stockbroker and the author of the memoir, has sadly ended his legendary life.
If you haven't read Reminiscences of a Stock Operator yet, I highly recommend this book. Many world-class hedge fund managers highly recommend this book. Following the ups and downs of the protagonist's life, you can get a sense of the turbulent and vibrant American financial markets of more than a century ago and wonder why the world has such a genius like Vermeer.
He was in the primeval era of hedge funds, and he summed up the classic rules that many modern investors follow: you can only increase when you make money, you should stop when you lose money, do not underestimate the opinions of others or the so-called hedge fund insider tips, and a complete set of hedge fund strategies.
Even more impressive, Livermore was not only a theorist but also a practitioner. His trading career went from being worth millions of dollars when he bought a house in 1907 to $100 million in 1929!
A man who had lost his fortune in the stock market, he ended up playing the sad scene at the beginning of this article. What happened to Livermore? The literature has no specific records, but if you carefully analyze his trading habits, it is not difficult to find spider silk.
Livermore began his trading career at the Bucket Shop.
In the late 19th century, the American stock market was booming, and technological advances gave ordinary people far from New York the opportunity to participate in stock speculation in real time: automated quoting machines connected to telegraph lines could broadcast the latest trading prices on the New York Stock Exchange across the country at any time. At the time, many people wanted to participate in speculation, but lacked the funds to buy and sell stocks.
In casinos, there are automatic bidding machines where players appear to be trading stocks, but in reality they are in the size of an onion. For example, the latest bid for a stock is $80, and players can buy the onion with just a $1 deposit. If a price of $79 or lower appears on the bidding machine, sorry you missed the light; if the bidding machine draws $81, the player can make a profit of $1 or continue to wait.
-
How do the scammers in the stock casinos make their money?
In addition to taking advantage of the crowd's frequent mistakes, they also manipulate the market with certain brokers. For example, many players bet on $80 and the casino owner is referring to the fact that the New York Stock Exchange's partners pressured the stock price, and as soon as an automatic price of $79 was placed on the bidder, the casino took the big chip.
A young Livermore with little money, mixed up in the stock market, gradually learned to read tape to predict market prices based on quotes. At that time, there were no computers, no real-time K-string diagrams, and Livermore's read-only diskette was actually the prototype of technical analysis.
But I suspect that he also developed a bad habit in the stock casinos: betting too much.
From the perspective of Kelly's formula, the ultra-low collateral of the stock casino was in fact the gambler's killer bait. The leverage was so large that the bet was far beyond Kelly's optimal value, and the loss was premature. The trading collateral of the US formal financial markets at the time was also low.
Reading his trading history is simply mind-blowing. Stocks, cotton, soybeans, whatever was the ultra-high-leveraged full-stock operation, it certainly accomplished Livermore's legendary greatness and also brought him several bankruptcies. Luckily, with the help of several nobles, Livermore was able to seize several important opportunities to reach the top in 1907, 1915 and 1929.
However, the wise man thought, "It's a loss, and I suspect it was the trouble of betting too much that caused Livermore to lose all of his money just a few years after he hit $100 million".
If Livermore combined his Kelly-based money management approach with his superb market capture, what miracle would this genius create?
History does not exist if.
Liverpool has flown by like a meteor, maybe he was born decades earlier.
Theories of money management and risk control only began to take shape in the 1950s.
Kelly's formula states that a game with a large, low-volatility winning face can have a large bet. How, then, to quantify a winning face with a large, low-volatility winning face? A contemporary of Kelly proposed a famous indicator.
-
Sharpe ratio
In the 1950s, it was proposed that the ratio of expected returns to volatility be used as a measure of investment opportunities. In 1966, scholar William Sharpe proposed the famous Sharpe Ratio on this basis:
S = (R
r) / σ, where: R = expected return on investment (mean rate of return) r = Rate of return on risk-free investments (understood as the rate of return on invested government bonds) σ = standard deviation of return (the most commonly used statistical indicator for measuring volatility) The higher the Sharpe ratio, the higher the quality of the investment opportunity.
A-investment: Excess (exceeding national debt) returns expected at 10%, standard deviation at 20%, Sharpe ratio at 0.5 B-investment: Excess returns expected at 5%, standard deviation at 5%, Sharpe ratio at 1
At first glance, A-investments with high return expectations seem to be a better opportunity. In fact, B-investments are usually better than B-investments because of their high Sharpe ratio, which means that investors can expect more returns in exchange for a one-unit hedge of risk. The same conclusion can be drawn from the perspective of leveraged investments: assuming that investors finance with an interest rate of r loans and add 1 times the leverage on the B-investment opportunity, then a leveraged B-investment becomes a 10% return expectation, a 10% standard, the same as the bad return expectation of A-investments, and the risk is lower.
-
Sharpe's ratio is high enough to be a good one.
Let's look at a real-world example: the long-term average annual return of the US stock market is about 10%, the volatility is about 16%, and the risk-free rate is about 3.5%, so the Sharpe ratio is about 0.4 (source: Wikipedia).
For retailers with long-term investments, the risk/reward ratio of investing in stocks is a thing of the past. If you are a hedge fund manager, this Sharpe ratio is too low: assuming you are aiming for a 20% annual return, you must leverage 2.5 times (return expectation = 2.5).10% - 1.53.5% ≈ 20%), which means that the average return for one year in six years will be less than 2.5* (10% - 16%) - 1.5*3.5% = -20%; you lose more than 20% and the customer is probably running out.
Generally, a Sharpe ratio greater than 1 is a good bet. This opportunity is rare in a simple hedge fund, so professional investors often use hedge funds to transform their hedge fund games to increase the Sharpe ratio.
For example, if you invent a way to hedge a Sharpe ratio of 2 against a variety of assets, you can leverage it boldly (your math classmates can calculate the probability of losing money themselves), and investors will probably go after your hedge fund.
However, hedge + leverage investing methods often have a practice threshold: borrowing a lot of money, high liquidity requirements, and therefore often problems in the face of a sudden crisis, as analyzed in the example of LTCM and Goldman Global Alpha Fund in the Wall Street Journal.
The Sharpe ratio is also flawed in that it assumes a normal distribution of returns, whereas the actual investment return distribution has a fat tail (the probability of losing a lot of money is higher than the normal distribution estimate), so there is a problem with simply selecting investment opportunities based on the Sharpe ratio, which can be easily manipulated. This topic is not discussed here.
For the average investor, the Sharpe Ratio suggests that they should consider the risks and rewards in terms of selecting a highly volatile investment. This is the point that was mentioned in the previous article: the game that is returning should be chosen with low volatility, the game with negative returns should be chosen with high volatility if you want to play.
Sharpe's ratio is about how to choose a betting strategy, and Kelly's formula is about how to bet on a game to get the best long-term return. Now let's combine the two methods and see if the 21-point count is the way to get rich.
Additional information on the Sharpe ratio
When it comes to the Sharp Ratio, the problem is concentrated in several areas:
The first question: how do you calculate that in the example of the US stock market, you have a return of less than -6% in an average of six years?
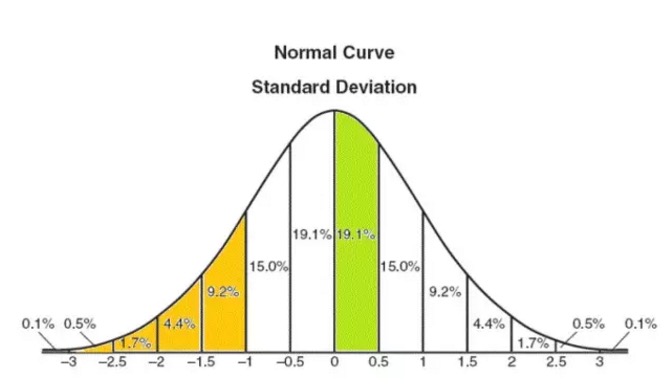
The Sharpe ratio assumes that the return on investment corresponds to the normal distribution (see figure below). Mathematically, the sum of a large number of independent random events generally corresponds to the normal distribution. For example, the sum of the results after a continuous toss of a coin, positive 1, and vice versa, negative 1, corresponds to the normal distribution.
The assumption of a normal distribution is not perfect, but it is a basic framework for understanding the problem. The following graph shows the probability values of a normal distribution. For example, the probability of a return between 0 and 0.5 standard deviations is 19.1% (green section of the graph).
Similarly, the probability of a return less than 1 standard deviation (orange in the graph) is about 16%; for the US stock market (average return 10% standard deviation, 16% standard deviation), the probability of an annual return less than 1 standard deviation, i.e. 10% - 16% = -6% is about 1/6.
The second question is: Is there anything that the Sharpe ratio assumption does not fit into reality?
Of course, the assumption of a normal distribution is not perfect. In fact, stock market movements are not completely random, otherwise we don't need to bother to study any laws. For example, in the financial crisis, stock market movements have a strong serial correlation, the so-called "serial correlation", which results in the actual stock market returns having a soap-tail phenomenon, i.e. the probability of the stock market moving to the extreme position is higher than the estimate of the normal distribution.
In addition, the risk-free rate of return r in the Sharpe ratio is a vague concept, and the cost of financing for investors is not r. Furthermore, the calculation of volatility is not a simple matter.
The third question is: What is the use of Sharpe Ratio for the average investor?
The next time someone tells you that my average return over the past three years is 30%! Well, you can ask yourself a question: How much fluctuation is there? Well, in the next blog, we will look at a real example of a hedge fund.
Analysis of the performance of hedge funds
The following table shows the average annual returns of several well-known large hedge funds (source: HSBC Research Report). All of these funds have assets under management of more than $1 billion and have been open for more than 5 years. Which fund would you invest in?
-
Table 1
| – | – |
|---|---|
| - | Compound annual rate of return |
| Fund A | 14.15% |
| Fund B | 15.17% |
| Fund C | 15.20% |
| Fund D | 79.17% |
| Funding E | 2.78% |
Congratulations, you have chosen the Paulson Credit Opportunities Fund, which has been in business for billions of dollars and has become one of the most well-known fund managers in the financial crisis. Paulson, who founded and manages the fund (his name is the same as former US Treasurer Paulson, but he is not related to him), is also one of the most famous fund managers.
But we have just discussed: not only the return, but also the risk. Table 2 lists the volatility of the funds and the Sharpe ratio estimates (assuming a risk-free return of 3%), what do you think after seeing them?
Table two
| - | Compound annual rate of return | The volatility of the rate of return | Sharpe ratio |
|---|---|---|---|
| Fund A | 14.15% | 5.94% | 1.9 |
| Fund B | 15.17% | 12.30% | 1.0 |
| Fund C | 15.20% | 4.53% | 2.7 |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 |
| Funding E | 2.78% | 12.21% | <0 |
In terms of volatility and the Sharpe ratio, the situation is a bit complicated. Fund C has a return of only 15%, but the volatility is less than 5%, so the Sharpe ratio is as high as 2.7, which is almost twice as high as the 1.5 of the Bolsonaro Fund! In other words, the volatility of Fund C is only one tenth of the volatility of the Bolsonaro Fund, assuming that the investor is only willing to take on a fixed volatility risk, then he can invest $1 in the Bolsonaro Fund or $10 in the C Fund, the risk is almost the same, while the total return of the investment Fund C is higher!
Fund C is Millennium Intl Ltd (millennium fund), an evergreen tree in the hedge fund industry, and its managers have had several Chinese high-profile managers. From the investor's point of view, whether to choose a profitable Paulson Fund or a stable millennium fund is a bit difficult to choose. In addition, Fund A and Fund B have sharp ratios significantly higher than the US stock market of 0.4, and also a good investment option.
Further analysis, comparing only the Sharpe ratio, seems unfair to the Paulson fund's yield: although its volatility is high, it is mainly upwardly volatile, which is not actually a risk. Investors are afraid of losing money, especially if they lose tens of percent. Therefore, the risk should also be measured by considering the maximum falling yield of the fund, i.e. the largest percentage of the funds that have fallen back from the highest point in history, see Table 3.
Table three
| - | Compound annual rate of return | The volatility of the rate of return | Sharpe ratio | Maximum decline (time of occurrence) |
|---|---|---|---|---|
| Bluecrest | 14.15% | 5.94% | 1.9 | -4.83% (2003) |
| FORE (frontline capital) | 15.17% | 12.30% | 1.0 | -27.01%(2008) |
| Millennium | 15.20% | 4.53% | 2.7 | -7.24% (1998) |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 | -10.41%(2007) |
| Drake | 2.78% | 12.21% | <0 | -51.74%(2007-2009) |
Now it's even more interesting that the biggest drop of Fund A (Bluecrest Capital) was less than 5%, and it happened in 2003. The fund avoided major losses during the Great Recession of 2007-2008, which is quite attractive. Bluecrest and Millennium are both of the stable type, both escaping the sub-prime crisis, and both seem to be difficult to distinguish.
The three funds are therefore favored by institutional investors, with funds under management of $8.6 billion, $10 billion and $6.3 billion respectively. It seems reasonable that people can make a living as a hedge fund.
Fund E (Drake Absolute Return Fund) was also a large fund managing billions of dollars, but it suffered huge losses of more than 50% in the financial crisis, causing investors to lose confidence and withdraw their funds, so Drake now manages only $ 200 million.
Finally, if you look at Fund B, its long-term compound annual return of 15%, Sharpe ratio of 1, the overall indicator is good, and although it suffered a loss of 27% in 2008, it has successfully overcome the crisis. It can be said that Fund B has considerable strength, so it has also become a large fund managing several hundred million dollars.
From this real-life example of evaluating investment performance, we can see the usefulness of risk indicators such as the Sharpe ratio and the maximum decline. Beginner investors often have only high returns and no risk-averse dilemma. Both the Kelly formula and the Sharpe ratio actually tell us one thing: to find a balance between returns and risks.
Stock markets are risky and should be invested with caution. The information provided is for reference only and does not constitute investment advice!
This article is translated from the blog Piscadia.
- OkCoin China API error code requested
- 2.12 _D (()) Function and Timestamp
- python: Please be careful in these places.
- A synergistic understanding of intuition
- The hidden Markov model
- Interested in understanding the simplicity of Bayes
- 2.11 API: Simple example of use of Chart function (graph function)
- Details of the currency pair
- Beware of the Linear Mind Trap
- I've heard that reading like this can make a lot of money.
- 30 lines of code that takes you into the world of quantitative investing (python version)
- Gambling is a form of high-tech business
- The quantity-price relationship is an important indicator!
- A strong demand for the platform to add do-as-you-go retargeting
- How to read the Big Three financial statements in a way that's interesting and interesting?
- Mathematical thinking in investment finance, how many have you done?
- Why slippage occurs in programmatic transactions
- The core of money management -- the choice of leverage
- Financial knowledge
- Causes and uses of ionization rates
Not unusualThank you.