The hidden Markov model

The hidden Markov model

• One, get to know

  Today we're going to show you a simple application of HMM (Markov Model) to stocks.

  The hidden Markov model, which sounds high-end and doesn't know what it is at all, let's take a step back and look at the Markov chain first.

  Markov chains, named after Andrey Markov (A. A. Markov, 1856-1922), refer to a random process of discrete events with Markov properties in mathematics. Given current knowledge or information, the past (i.e., the current prior historical state) is irrelevant to predicting the future (i.e., the future state after the present).

  

  In this process, the transition of each state depends only on the previous n states, which is called an n-step model, where n is the number of states affecting the transition. The simplest Markov process is a one-step process, where the transition of each state depends only on the previous one.

• Two examples

  In mathematical terms, it looks like this:

  

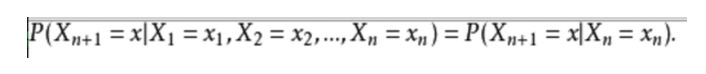
  To give an example from everyday life, we want to predict future weather conditions based on the current weather conditions. One way is to assume that each state of this model depends only on the previous one, the Markov hypothesis, which greatly simplifies the problem. Of course, this example is also somewhat impractical.

  

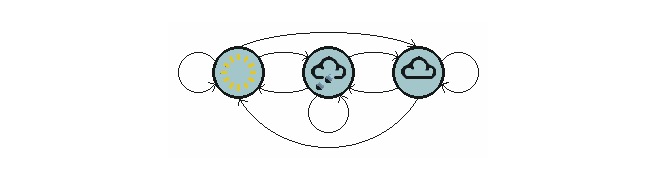
  The diagram above shows a model of the weather shift.

  Note that a first-order process with N states has N2 state transitions. The probability of each transition is called the state transition probability, or the probability of transition from one state to another. All of these N2 probabilities can be represented by a state transition matrix, as in the weather example above:

  

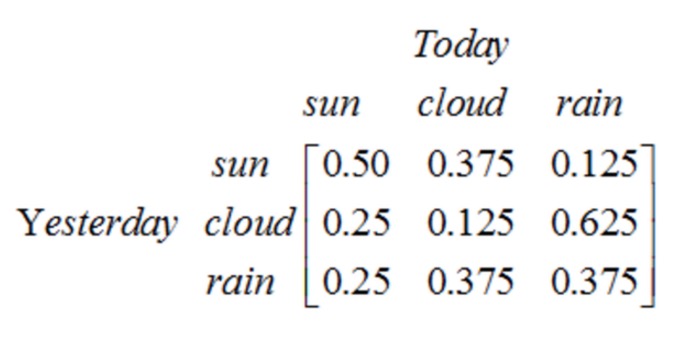
  This matrix says that if it was cloudy yesterday, there is a 25% chance of clear weather today, a 12.5% chance of cloudy, a 62.5% chance of rain, and it is obvious that the sum of each row in the matrix is 1.

  In order to initialize such a system, we need an initial probability vector:

  

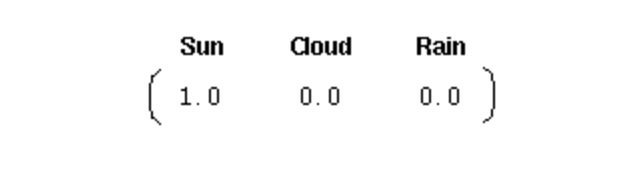
  This vector indicates that the first day is clear. Here, we have defined the following three parts of the first Markov process above:

  State: Sunny, cloudy and rainy.

  Initial vector: Defines the probability of the state of the system at time 0.

  State-shift matrix: the probability of each weather transformation. All systems that can be described in this way are a Markov process.

  However, what do we do when the Markov process is not powerful enough? In some cases, the Markov process is not strong enough to describe the patterns we hope to discover.

  For example, in our stock market, if we were merely observing the market, we would only know the price, volume, etc., of the day, but not what the current state of the stock market is (bull market, bear market, shocks, rebounds, etc.) in which case we have two state sets, an observable state set (stock market price, etc.) and a hidden state set (stock market condition). We hope to find an algorithm that predicts the state of the stock market based on the stock market price, volume, etc., and the Markov hypothesis.

  In the above cases, the observable state sequence and the hidden state sequence are probabilistically related. Thus we can model this type of process as having a hidden Markov process and an observable set of states associated with this hidden Markov process probability, the latent Markov model.

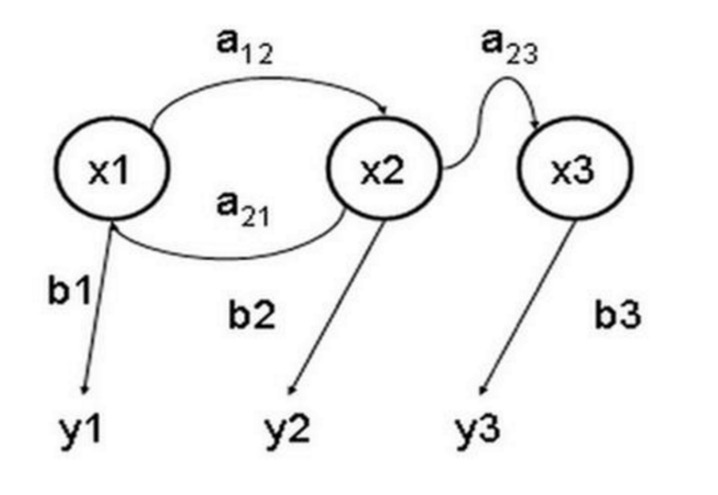
  The Hidden Markov Model is a statistical model used to describe a Markov process with implicit unknowns. Its difficulty lies in determining the implicit parameters of the process from the observable parameters and then using these parameters to perform further analysis. The following diagram is a three-state Hidden Markov model state transfer graph, where x represents the implicit state, y represents the observable output, a represents the state conversion probability, and b represents the output probability.

  

  To illustrate this with the example of a cube: Suppose I have three different cube in my hand. The first cube is our ordinary cube (called this cube D6), with six faces, each face (1, 2, 3, 4, 5, 6) with a probability of 1/6. The second cube is a quadrilateral (called this cube D4), each face (1, 2, 3, 4) with a probability of 1/4. The third cube has eight faces (called this cube D8), each face (called 1, 2, 3, 4, 5, 6, 7, 8) with a probability of 1/8.

  

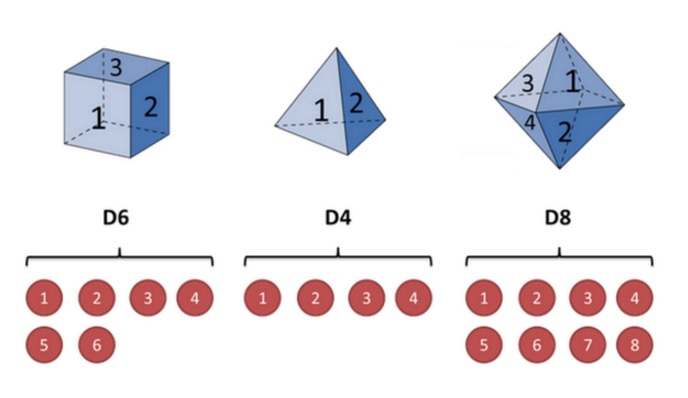
  Let's say we start with the dice, we pick one of the three dice, and the probability of picking each of the dice is 1/3. Then we pick the dice, and we get a number, one of 1, 2, 3, 4, 5, 6, 7, 8.

  This sequence of numbers is called the visible state chain. But in the implicit Markov model, we have not only the visible state chain, but also the implicit state chain. In this example, the implicit state chain is the sequence of the cube you are using.

  一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。

  Similarly, although there is no conversion probability between the visible states, there is a probability between the implicit state and the visible state called the output probability. In our example, the probability of a six-sided die (D6) producing 1 is 1/6. The probability of producing 2, 3, 4, 5, 6 is also 1/6. We can also make other definitions of the output probability.

  

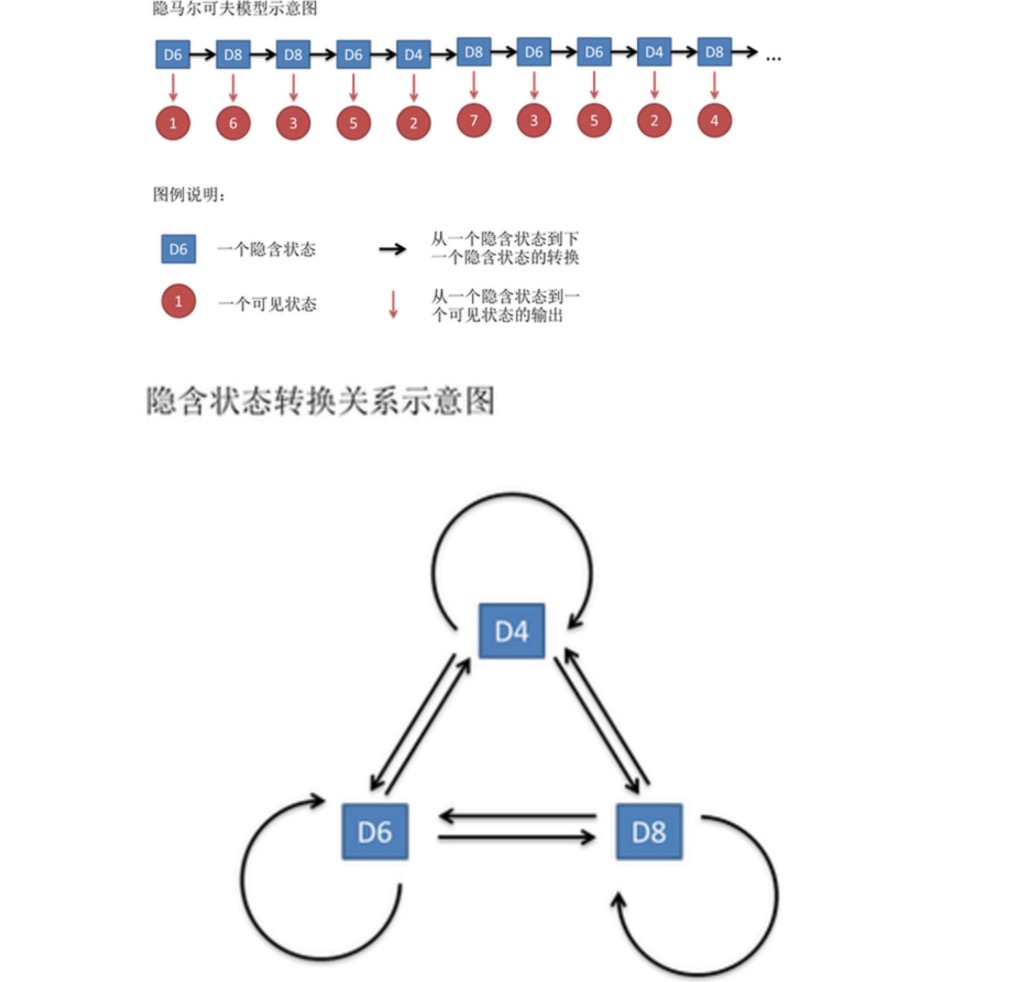
  In fact, for HMM, it is quite easy to do the simulation if you know in advance the conversion probability between all implicit states and the output probability between all implicit states to all visible states. However, when applying HMM models, there is often some missing information, sometimes you know there are several types of cages, what each type of cage is, but do not know the sequence of cages that come out; sometimes you just see the results of many cages, and the rest you do not know. If you apply an algorithm to estimate this missing information, it is an important problem.

  Algorithms related to HMM models are mainly divided into three categories, each solving three problems:

  • Knowing the number of monkeys (number of implied states), what each monkey is (conversion probability), and based on the results of the monkey's casting (visible state chain), I want to know which monkey is casting each time (implied state chain).

  • Also know that there are several types of monkey (number of implied states), what is the probability of each type of monkey (conversion probability), and based on the results of the monkey cast (visible state chain), I want to know the probability of casting this result.

  • Knowing that there are several types of monkeys (the number of implied states), not knowing what each type of monkey is (the probability of conversion), observing the results of many types of monkeys (the visible chain of states), I want to reverse what each type of monkey is (the probability of conversion).

    If we want to solve the above problems in the stock market, we need to solve problems 1 and 3.

Translated from the Knowledge of Moneycode column