A short history of risk (5) Bayes, a man who lives only in his textbooks

In this video, you can see a picture of a man who lives only in his textbooks.

** The work of Bayes, whose birthdate is unknown, continues to demonstrate the exciting idea that uncertainty is a measure of uncertainty, and provides us with a method of inferring unknown probabilities based on the experience of the objective world, which is the result of continuous modification of the information we receive.

** It is a very strange thing that a person as famous as Thomas Bayes in the entire history of science does not have anything to write about his personal life story. This shows that Bayes was very low-key during his lifetime, on the other hand, it brought me a great inconvenience for such a writer, because in fact everyone likes to see the quirks of scientists, such as bad communication at the same time arrogant, such as the interruption of the toy disillusionment is a surprise, and it can not be the case that the flowers are not interested in studying the arrow, otherwise they cannot fully reflect the uniqueness of the genius. **

• By Thomas Bayes However, Bayes was such a boring man. He was a non-mainstream clergyman living in the English countryside, and his work on weekdays was probably to organize the whole village to square dance, no, Mass, and it is said that the whole village loved him for it. The only thing that seems a bit legendary is that he, like many legends, did not publish a book while he was alive.

  When Bayes died, he left his manuscript plus £100 to a preacher named Prince. This Prince was also a strange man, and the construction of spiritual civilization and material civilization went further than Bayes knew. He felt that free will was a gift from God, and he wrote papers proving that American independence was also God's will.

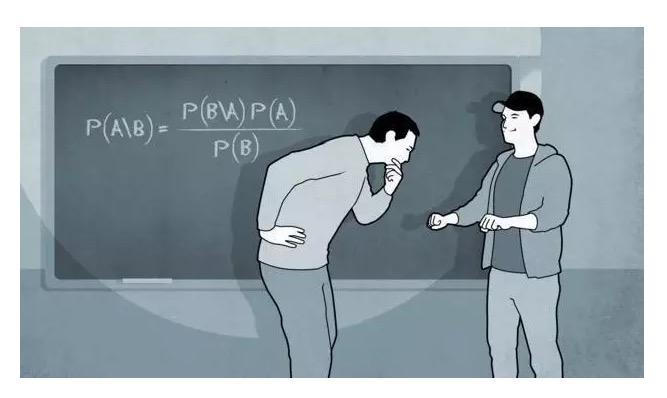
  Three years after Bayes's death, Prince helped him publish his obituary. But the timing of the paper's significance was faced by the academic community for another twenty years. In the paper, Bayes intended to explore the question: If we only know the number of times an event occurs and the number of times it doesn't, how should we calculate the probability of the event occurring in the absence of other information?

  Let's recall the previous example ("Risk Story 4": Tom Mover and the Curve of God".); for example, for a batch of products, if we take 10,000 products and find 12 of them to be waste, what is the probability that the waste rate is 0.1% for this batch of products? For real life, this question is undoubtedly more valuable to us, because everyone's observation of things is always limited, and we need to know to what extent what we see can reflect the truth, as if we were to touch an elephant, how do we determine if we are touching the whole elephant, the leg or the fat brother next to it?

  Bayes's method is actually to constantly modify old information with new information, increasing the credibility of the probability on the basis of the modification. This is the prior probability and the posteriori probability in the legend.

  

  If we hit a ball on the table, the ball stops at any point. Then, we hit another ball repeatedly, counting the number of times it rolls to the left and right of the first ball respectively. Of course, here you can reasonably ask the question, since we are going to hit the table, why not the second ball to hit the first ball, I think you asked a good question, but I just don't want to answer.

  In this example, the probability directly given for the first stop is the prior probability, and the probability of the first stop being modified based on the second stop is the posterior probability. That is, the Bayesian method is that our cognition is limited by our cognitive ability, so we need to constantly update our view with updated information.

  The above sentence is probably the most compelling one yet. Let's assume an example to help us understand:

  If you have opened two malls in your city, and the traffic of people in the new mall accounts for 60% of the total traffic, then at this time any customer has a 60% probability of being a customer of the new mall. This is the prior probability. And the old mall facilities are poorly managed, the staff also lack training levels, and the complaints received are twice as high as the new mall.

  

  The simplest answer is to ask where the person is. Of course, the person will most likely answer that you guess (too low), so how can you guess that there is a greater chance of correctness? If from a preliminary probability, then you should find a manager for the new mall, because the new mall has more traffic than the old one. But from the complaint, the new mall only accounts for 1/3 of the total complaints.

  Bayes, whose birth name is unknown, now appears in virtually all statistics, artificial intelligence, game theory, and genetics textbooks, causing countless problems for many university final exam candidates. His work continues to demonstrate the exciting idea that uncertainty is a measure of uncertainty and also provides us with a way of inferring unknown probabilities from the experience of the objective world, which is a result of constantly adjusting the information we receive. This way of thinking is inconsistent with the goals of our risk management and practice: in a dynamically changing market, if uncertainty exists, any outcome and decision-making depends on our inference of the latest and most comprehensive information, and such inference is equally endless.

Translated from Chinese Quantitative Investment Society