Trading strategies of gamblers

Trading strategies of gamblers

The practical content of this article can be seen in Mark Wahlberg's latest film, The Gambler (2014). The subject of this article is actually a quote from Jobs: "We're making it less random to make it feel more random".

The following paragraphs are for introduction, and the author recommends that you read the original text patiently after reading the introduction, so you can better understand the wisdom of Joe's assistant.

• The most often quoted sentence in the Declaration of Independence is: "All men are created equal". However, rather than being a statement of fact, it is closer to the pledge we make when we bow our heads in prayer at the Shrine: "We want all people to be born equal".

  The vows imply that this doesn't exist: someone is running from a stroller, someone has an IQ of 180, a pencil calculator and a skinny body at the age of three.

  The inequality we're going to talk about today is even more unbalanced than the above: Why does someone always win?

  Every company has a few of these people, and every year's lottery, they take the prize on the stage, saying that they are not attached to money. I once bought a coffee and bought one, and got the one opened, and bought one, and couldn't sleep at night (of course, it could also be too much caffeine).

  This is the only experience that can be described as winning consecutive awards.

  It's unfair to win consecutive awards and it always happens to the other person.

  Assuming the company has 200 people, the probability of winning the top prize in the annual lottery is 1/200 = 0.5%, and the probability of winning the top prize for two consecutive years is 0.5% x 0.5% = 25 millionths, which is low enough.

  But in fact, it is the probability of a particular person (you) winning the top prize two years in a row. The probability of any one person winning the top prize two years in a row is 200 x 0.5% x 0.5% = 0.5%, which is the same as the probability of winning the top prize once in a draw.

  Let's relax a little bit. The probability of one person winning twice in three years is 1 - the probability of three different winners in three years is 1-200 x 199 x 198 / 200 x 200 x 200 = 1.5%.

  In other words, if you think it's okay to give me a first prize in three years, then it's okay to bite someone's handkerchief on stage and win two first prizes in three years.

  I'll give you a whole year's supply.

  What's even more outrageous than the guy who won consecutive awards at the same annual awards when he was the one who won the May Day award?

  Going back to the example of a company with just 200 people, let's say there are 10 prizes and the employee can repeat the prize. So the probability of any one person drawing more than two prizes is: The probability of winning 10 prizes by 10 different people is 1-200 times...x191/(200 times...x200) = 20.4%

  There's a one in five chance that a colleague will tell you that you won the prize and I won it... my feet are a bit sour.

  London traders: The focus is now

  Randomness is not random

  This seems unlikely, but it is really such a crazy phenomenon in life, that is, it is like randomly playing a song, if you do not remove the listened to song from the playlist, the playlist of 10 songs, try to listen to 10 songs in a random order (i.e. no song repeats) after listening to 10 songs, only 10!/1010 = 0.036%, less than the chances of impossible tasks, and also less than Tom Cruise's chances of not getting divorced.

  Apple's random playback program is said to play different singers, mixing different tunes, and allowing users to feel that each song is unrelated ("a fairly random blend of non-random human intervention"). Jobs once said, "We're making it less random to make it feel more random".

• All right, ready to go, ready to go, now start writing.

  Speaking of the gambler model of trading (concrete case studies can be seen in Mark Wahlberg's latest film The Gambler, but London traders say the film doesn't look good)

  When trading, whenever I guess a direction, if I get it wrong, I double the position in reverse, the price always comes back, it is impossible not to go backwards (not fall backwards).

  If you lose 1 dollar, don't worry, next time you bet 2 dollars, if you win you win 4 yuan, more 1 yuan, if you make a mistake again you bet 4 yuan, return is 8 dollars, total investment 1 + 2 + 4 = 7, or win 1 dollar.

  This is the way to calculate, you don't need to know, every time you are stable 1 yuan.

  Come on! Come on! I always make money at the end!

  This classic gambler's fallacy, like the Ponzi scheme, has a remarkable vitality, longevity and staying power, and has deceived generations of speculators.

  The probability or expected value of a positive coin roll is 0.5, but if it is rolled only once, the probability of a positive coin roll is 0 or 1 ((far off 0.5)); as the number of rolls increases (i.e. the sample increases), the probability of a positive coin roll gradually approaches 0.5;; but according to the axiom of the law of the pyramid of cognitive psychology, the effect of sample size is usually ignored, assuming that the small sample and the large sample have the same expected value.

  After many positive experiences, you always feel that the opposite is more likely to happen.

  On the roulette wheel's dice table, there is always a large number of gamblers who choose to bet on black after red has appeared several times in a row.

  If you use this strategy, the funding curve will inevitably look like this:

  

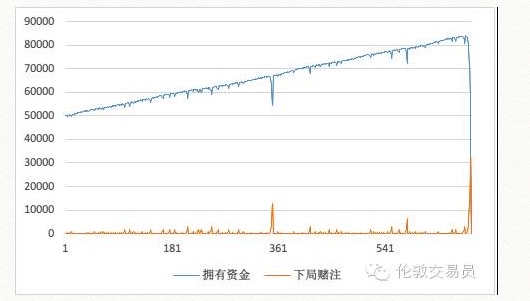
  In practice, the capital curve is all the way up, and it seems to be stable. When the practice is close to 361 times, we can see that one mistake in a row, and then stick to the strategy, not only goes backwards, but also continues to arrogate all the way upwards.

  Of course, the end result of such tactics must be zero, bloodless. Not only bloodless, but also with a strong painful feeling of a broken dream.

  I've seen this happen more than once. Every time someone announces a new deal to me that has almost no reversal, I wonder if someone else is playing the gambler's fallacy.

  The so-called grid trading strategy, the Martingale method, etc., can never escape the grip of the gambler's fallacy, but it will inevitably gain eternal vitality.

  Because it is never the ability to make a profit that determines the popularity of a strategy, but rather whether it is appropriate for human nature.

  Anything in the world, it seems, will gain a stubborn vitality as long as it meets human expectations. It's like the Ponzi scheme. The grid strategy is good, the Martingale strategy is good, it always gives you a very, very stable return at the beginning.

  The human brain abhors loss far more than it gains. This is a strategy that our ancestors evolved in ancient times, because our ancestors on the prairies could come and fill their stomachs and finish the meal.

  However, human civilization is developing at a rapid pace, the brain in the biological sense is still evolving in millions of years as a unit. How can an ancient brain cope with today's financial markets?

  (Recommended book: Neuroeconomics, Second Edition)

  If you are being advised of a stable, no-loss trading strategy and the promoters are confident that you do not need any market insight to manage your money as your main trading rule, then be careful, it is likely another version of the gambler's fallacy.

  The financial markets are a bit like thermodynamic systems, and we need to keep in mind the conclusions that thermodynamics provides to prevent us from being cheated.

  The most important is the law of conservation of energy, which states that energy cannot be created in a vacuum, nor can it disappear in a vacuum. In the market, it is impossible to make a profit in a vacuum without contributing or having insight, without making the market more efficient and resourceful, which is against the laws of nature.

  There is no strategy that violates the laws of nature, that's for sure. Any effective strategy must have the advantage of information asymmetry, or superhuman insight, or use your own resources to make the market more effective.

  The net trading strategy (which is doubled if you are wrong) of pretending not to provide any output to get a profit is like trying to build a perpetual motion machine, which is a dream of a maniac.

  Without taking into account the cost of the transaction, the net strategy (i.e. doing one thing at a time, never stopping losing a position, making a profit immediately if it's right, doing the opposite if it's wrong, doubling a position) has zero expected return.

  This expected return of zero is purely mathematical, and given the transaction costs, the expected return is negative, i.e. a losing strategy.

  Again, given that the grid strategy says that the additional investment required is in line with the profitability model, even after making a few mistakes, the new investment required will be astronomical.

  The financial capacity, in the end, has a limit, because the existence of this constraint, a less wonderful end is inevitable.

  Everyone understands the law, it's hard to stick to it.

  But but!!! After saying that we have not eaten bread for so long, everyone looks disappointed, and we understand the deceit of the gamblers, let's see what the wise man called the trick.

  This is a wonderful post from a netizen on Everybody's Net:

  A fair game in every way: a simple mechanical device, with two slots for black and white; the player puts in the respective betting coins (the equivalent of one dollar in cash); the machine starts to run until all the players have finished betting, and a ball is randomly dropped from two black and white holes; the loser is empty, the winner has a double prize.

  I realized that this stalemate is equivalent to saying that the boss has 1 chance of winning each of the 1/2 mutually exclusive events. Under this model, no matter what mixed strategy the player adopts, the expected return is always zero.

  I have no idea how to win, and I don't think it's possible.

  Sjun then goes on to say that his strategy is simple. Choosing a color, such as black, at once. He bets one coin on black first; if he loses, he bets two coins on black again; if he loses again, he bets four coins on black a third time.

  The advantage of this method is that no matter how much money you have lost, you can reverse the loss by winning once, with a net profit of 1 yuan, and the probability of n consecutive losses is very small, only 1/ ((2 ^ n)).

  Of course, this approach is not enough for me. When I said before that any mix-up strategy is expected to be zero, I naturally included this strategy.

  This strategy seems to have a small probability of losing, why is the expectation zero? It is simple, because his bet is too big, assuming he loses the first 7 times, then the eighth time he has to hit 256 yuan before he can double down. But the eighth time he loses again, he has a cumulative loss of 511 yuan, and I don't think there is a newborn S capital that continues to slump. In other words, although the probability of failure is small, but the loss is also fatal when every seven or eight small unlikely events occur, so that he can continue the game for several weeks.

  To be honest, I very much doubt the feasibility of this strategy.

  From the text to this point, we can see that this is a simple strategy like the grid strategy, a classic form of the gambler's fallacy.

  In fact, however, Mr. S did adopt this strategy, every time he made 20-30 coins in the game room, and then went to play other games in the afternoon. Not only did I completely believe his words, but his later analysis made me believe that this strategy really worked, because my previous analysis made a fatal mistake.

  You've made a fatal mistake in believing that this is a perfectly fair game.

  Here comes the fun part, the super dry goods.

  What do you mean?

  Sjun smiled and said, "Your analysis is perfect from a mathematical point of view. But don't forget, your conclusion is that the player's expectations are zero, in other words, the landlord's expectations are also zero. But is the landlord's income really zero, and if it is zero, is it not a loss that he bought this machine to teach the rent?"

  In fact, Mr. S's idea was that the landlord must be making money. The only way is for the landlord to manipulate the small ball. To make an extreme assumption, if someone bets 10,000 on white, then the probability of his winning is very small, the landlord will not sit and watch the flow of water for weeks. Although there is no one in the slot machine room to win 10,000, according to S, it is not uncommon for adult landlords to win 200-300 at a time.

  For the landlord, the most greedy situation is to manipulate the small ball every time it lands on the smaller color of the bet, so that it bounces every time. But this is obviously not normal, and if it is too obvious and realized by the player, it can not be a pleasant game.

  The landlord should win or lose, and generally maintain a decent small return, such as 10% per tenth of the turnover, although not much, but still be profitable compared to any financial asset.

  I'm a little skeptical: hey, so for players, you should always be on the side of the minority, that's not your strategy either.

  S goes on to say that the machine is set up so that each player puts a coin in front of the other. Without interaction with the player, it is basically impossible to see the other players put the coin in that place, and it is impossible to make decisions again every time they interact with other players.

  Me: Why is it that the rule of the few wins doesn't make any real sense?

  S: You can't look at the game in isolation. In fact, when you realize that the game has hidden rules, you've already gone a lot further than before.

  Me: There's more, I think the few wins are enough to make the boss money.

  S: The owner of the machine has already borne the costs of the machine and the venue, that is, he is in debt in this game. He not only cannot lose money, but he must also make money. And to make money there are two necessary conditions, one is not to let someone withdraw a large amount of money at a time, which is what is called a few wins, but the other important condition is that the machine attracts as many players as possible on the premise of a stable income.

  I: From the gambler's point of view, the game is tax-free and the winnings seem to be half and half, but in fact it is very tempting.

  S: Well, but other players who don't have a mathematical mindset don't see it that way. Let's go back to the beginning of your question, you said that my strategy is not likely to fail, but if it fails, it will lose badly, right?

  Me: Oh yeah, even though the probability of failure is only 1/ ((2^n), but once it fails, you lose 2^n or so.

  S: Well, you might want to think carefully about the situation where I might fail. I usually have around 300 yuan in my hand, enough to support me from press 1 to press 128 yuan, which is eight times.

  Me: Well, it's a small possibility, but it's there... and it's a big loss...

  S: Oh you're wrong, this probability only exists in mathematics. In fact, it's impossible that the boss won't allow this to happen. Try it in a game, once the same color appears eight times, for me, it's acceptable, because I've played a thousand times, eight times the probability of white is 1/128.

  The goal is not to make players question the game's manipulation, but rather to make them feel that they are not manipulated.

  Based on this principle, even small probability events under the normal distribution must be removed because they raise questions ("because fairness makes one feel unfair"). In contrast, the occasional manipulation of a few minority plates by the hot-water frog method wins because the landlord does not know beforehand that white and black are minorities, so the result does not seem to break the black-and-white average distribution.

  So the landlord does not hesitate to let the few win, because this trick does not break the intuitive black-and-white balance. But it is absolutely not allowed that there is a lot of consecutive occurrences of the same colored dice, although in a large number of games such a small probability event should occur.

  They are small probability events in mathematics, but are modified to zero probability events in reality.

  It is only now that I fully understand where S is really sharp, and why such a simple strategy can always win in such a fair game.

  Later, S added that he thought that the boss deliberately controlled 10% of the earnings was too much trouble, after all, the boss also had to take care of other games and players. So the closer to the fact is that the machine itself has a random distribution. In this distribution, the boss's earnings are indeed the same as the players as a whole, zero. And the boss only takes a period of time each day, manipulating several games, so that the boss always earns enough money in these games, the rest of the time the machine runs automatically.

  S's strategy is not only effective against greedy bosses, but also against seemingly fair machines. The logic is simple: it is a machine from a decade or so ago, with electronic components inside, but it is more of a simple mechanical device. In fact, no one who makes a machine, including a computer, can truly express the randomness of randomness, and the random number in any program is essentially a pseudo-randomness with complex operations.

  However, for simple machines, simulating dozens of scenarios is very expensive, and it is unnecessary to assume that the machine only stores the entire canvas of the five-player game, black black black black black black black, white black black black, white white black black black... white white white, white white, white white, etc., i.e. 2^5 = 32 scenarios, which is random enough and fair enough for the occasional player to eliminate S.

  For S, if the machine only stores these 32 situations and calls them repeatedly, his strategy will always win as long as he prepares the necessary five bets of 1+2+4+8+16=31 yuan.

  In fact, S buys more than 30 coins on the first deposit. Each time he invests in these coins, he earns an additional 20-30 coins to play the game he really wants to play. That is, the machine's reserve is indeed less than 32 hours.

  It was then that I realised how big my thinking gap was with S, that all my judgments were based on mathematics, and that this part was a total waste of what had been solved in the previous two or three hundred words, but that the last few thousand words were the area where S really thought.

  The first time I read this post, it was like a waterfall, a miscarriage and a bone transplant!

  After all, it's a game of chance, and I've been immersed in a quantum world of numbers, searching for strategies that will hopefully yield higher returns, while ignoring a basic fact that's right in front of me:

  Quantification is always just a means and a method, the trader is after all trading with a human being. The so-called transaction is done with a trading partner and you. The speculative market is a game with a human being, not a formula.

  If you realize this, the words behind it are not difficult to understand.

  S says that sometimes there are emergencies or other reasons, he does not have time to come to the game coin flower to go home. He rarely finds the owner to exchange the remaining coins for money (in principle, it is possible). But considering that he has to repeat this strategy, it is not really possible to greedily make the boss doubt that he will choose a game that is mathematically obviously going to lose the coin quickly.

  This is the story of S.

  The wise S-king must have understood the information advantage of the boss, as the casino owner of the trading opponent has the power to stop the game, and the wise strategy is to say goodbye.

  Only a higher level can beat your opponent, only different insights can get the profits they deserve.

  The desire to make a profit in vain, without working hard, is the root cause of being deceived.

  Is there a profit strategy in the world that doesn't judge price movements?

  Yes, but they succeed because they contribute, not because they work hard.

  To give a simple example, London gold, New York gold, and Shanghai platinum all have exactly the same chemical properties.

  However, since the two are traded on different exchanges, a strategy known as "cross-market arbitrage" has been developed. This strategy exploits the "one-price arbitrage", which means that the same thing can only have one price at a time.

  Institutions with trading advantages, using their IT and financial advantages, preempt price deviations by selling high-priced gold and making more low-priced gold products. For information on IT technology and high-frequency strategies, see the article "The Wolf of Wall Street (High-Frequency Real War) "

  The price will inevitably come back, then this combination of investments will be profitable, regardless of whether the price of gold falls in the future, it can be profitable. If the price of gold rises in the future, then the low price of gold earns more money than the excess of high price to make a loss of position, and vice versa.

  In this case, the government is not the only one who is trying to make the market more efficient, because the agency is outsourcing its resources to help the market be more efficient and thus get the return it deserves.

  Again I warn you: bread will not fall from heaven.

  As London traders have repeatedly emphasized, if you don't know the business, where your strengths are, why others need you, where your limits are, why you're not profitable, be clear about it.

  It's better not to make a trade if you don't know what to do than to stop a trade in time. Of course, if you've already made a trade and you have a problem, or stop a trade in time, that's a survival condition.

• I'm going to summarize:

  Don't believe that the so-called bonus and return strategies can produce real returns unless you have insight into the point of origin of the Ponzi scheme.

  There is always a doubt about any promise of higher interest rates.

  As with the grid strategy, there is no backward strategy, so be careful. Why does it perform so well, what are its advantages? What resources or knowledge does it have that others don't have?

  If there is no extraordinary idea or resource, it is bound to be rejected by the market.

(This article was originally published by London Trader)