En este artículo, vamos a describir el proceso Ornstein-Uhlenbeck, describir sus fórmulas matemáticas, implementarlo y simularlo con Python, y discutir algunas aplicaciones reales en finanzas cuantitativas y transacciones de sistemas. Usaremos un modelo de proceso aleatorio más avanzado, llamado proceso de Ornstein-Uhlenbeck (OU), que se puede usar para modelar secuencias de tiempo de regresión que muestran comportamientos de regreso a la equivalencia.

¿Qué es el proceso Ornstein-Uhlenbeck?

El proceso de Ornstein-Uhlenbeck es un proceso de aleatoriedad en tiempo continuo utilizado para modelar el comportamiento de la regresión de la equivalencia. Esto significa que, a diferencia de los desplazamientos aleatorios estándar o el movimiento de Brown, que pueden derivarse indefinidamente, el proceso de OU tiende a regresar a su promedio a largo plazo con el paso del tiempo. En términos matemáticos, el proceso de OU es la solución de una ecuación de diferenciación aleatoria específica (EDS) que controla este comportamiento de la regresión de la equivalencia. El EDS del proceso de OU se da por la siguiente fórmula:

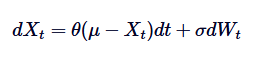
De ellas, Xt representa el proceso aleatorio en tiempo t, μ es el promedio a largo plazo, θ es el promedio de regresión, δ es la volatilidad, y dWt es el proceso de Wiener o el movimiento estándar de Brown.

Contexto histórico y aplicaciones

El proceso Ornstein-Uhlenbeck fue propuesto originalmente por Leonard Ornstein y George Eugene Uhlenbeck en 1930 para simular la velocidad de una partícula en movimiento browniano en condiciones de fricción. Con el tiempo, su utilidad ha ido más allá de la física, con aplicaciones en diversos campos como la biología, la química, la economía y la finanzas.

En finanzas cuantitativas, el proceso OU es especialmente útil para modelar el fenómeno de la regresión de la media. Ejemplos notables incluyen la volatilidad de las tasas de interés, los tipos de cambio y los mercados financieros. Por ejemplo, el popular modelo de tasas de interés, el modelo Vasicek, se deriva directamente del proceso OU.

Importancia en las finanzas cuantitativas

El proceso de Ornstein-Uhlenbeck es fundamental en la finanza cuantitativa por las siguientes razones: su naturaleza de regresión de la mediana lo convierte en una opción natural para el modelado de variables financieras que no muestran un comportamiento de desplazamiento aleatorio, sino una oscilación de la mediana a largo plazo en torno a la estabilidad. Esta característica es fundamental para el modelado de tasas de interés, donde la regresión de la mediana refleja el impacto de los bancos centrales en la estabilidad de las tasas de interés a largo plazo.

Además, el proceso OU también se usa en modelos de precios de activos (incluida la valoración de derivados) y estrategias de gestión de riesgos. También puede servir como un componente de modelos más complejos, como el modelo Cox-Ingersoll-Ross (CIR), que extiende el proceso OU para modelar tasas de interés con valores no negativos.

Principales características y intuiciones

Las principales características del proceso Ornstein-Uhlenbeck pueden resumirse como sigue:

• Regresión del promedio:El proceso OU tiende a regresar a la media a largo plazo μ. Esto contrasta con procesos como el movimiento de Brown, que no muestran esta tendencia.
• La volatilidad:El parámetro δ es el nivel de aleatoriedad o volatilidad en el proceso de control. Cuanto mayor sea la volatilidad, mayor será la desviación del promedio del proceso antes de regresar.
• Velocidad de regreso:El parámetro θ determina la velocidad a la que el proceso regresa al promedio. Cuanto mayor sea el valor θ, más rápido regresará al promedio.
• Estabilidad:El proceso OU es fluido, lo que significa que sus características estadísticas no cambian con el tiempo. Esto es fundamental para modelar sistemas estables en el ámbito financiero.

Intuitivamente, se puede considerar el proceso de Ornstein-Uhlenbeck como un modelo del comportamiento de la corteza adiposa que se extiende alrededor de la media. Aunque el proceso puede desviarse de la media por fluctuaciones aleatorias, la columna de fricción de la corteza adiposa (similar a la regresión de la media) asegura que finalmente regrese a la media.

Comparación con otros procesos aleatorios

Debido a que el proceso OU está estrechamente relacionado con la modelación de diversos fenómenos financieros, a menudo se lo compara con otros procesos aleatorios (como el movimiento Brownian y el movimiento Browniano Geométrico (GBM)). A diferencia del movimiento Browniano (donde el movimiento Browniano no tiene tendencia a regresar a la media), el proceso OU tiene un comportamiento de regreso a la media evidente. Esto lo hace más adecuado para modelar escenarios en los que las variables oscilan en torno a un equilibrio estable.

En comparación con el GBM, que se utiliza generalmente para modelar el precio de las acciones y que contiene elementos de derivación y fluctuación, el proceso OU no muestra un aumento en el índice, sino una oscilación en torno a su promedio. El GBM es más adecuado para modelar cantidades que crecen con el tiempo, mientras que el proceso OU es muy adecuado para modelar variables que muestran características de regreso en el promedio.

Ejemplos de finanzas cuantitativas

El proceso de Ornstein-Uhlenbec tiene una amplia aplicación en el campo de las finanzas, especialmente en escenarios de modelado donde la regresión de la media es una característica clave. A continuación, discutiremos algunos de los casos de uso más comunes.

Modelado de las tasas de interés

Una de las aplicaciones más destacadas del proceso OU es para la modelación de tasas de interés, especialmente en el marco del modelo de Vasicek. El modelo de Vasicek asume que las tasas de interés siguen el proceso OU, es decir, que las tasas de interés tienden a regresar a su promedio a largo plazo. Esta característica es crucial para simular con precisión el comportamiento de las tasas de interés, ya que las tasas de interés tienden a no fluctuar indefinidamente, sino que fluctúan cerca de un nivel promedio influenciado por las condiciones económicas.

Precio de los activos

En la valoración de activos, especialmente de los títulos de renta fija, el proceso OU se utiliza a menudo para simular la evolución de la rentabilidad de los bonos. La naturaleza de la regresión de la media del proceso OU asegura que la rentabilidad no se desvía demasiado de su media histórica, lo que coincide con el comportamiento observado en el mercado. Esto hace que el proceso OU sea una herramienta valiosa para la valoración de bonos y otros instrumentos sensibles a la tasa de interés.

Estrategias para el comercio de pares

El pairing trading es una estrategia de neutralidad de mercado que consiste en establecer posiciones de compensación en dos activos relacionados. En este caso, el proceso OU es especialmente útil porque permite modelar la diferencia de precios entre los dos activos, que suele ser la regresión al promedio. Mediante el uso del proceso OU para modelar la diferencia de precios, los operadores pueden confirmar los puntos de entrada y salida de ganancias cuando los precios se desvían de su promedio, y predecir la regresión al promedio, generando así una señal de negociación.

Por ejemplo, si la diferencia de precios entre dos futuros se extiende más allá de un determinado punto de desvalorización, el comerciante puede cancelar los futuros de excelente rendimiento y hacer más de los de bajo rendimiento, con la esperanza de que la diferencia de precios vuelva a su promedio histórico, lo que permite obtener ganancias cuando ocurre la reversión.

La solución de la SDE de Ornstein-Uhlenbeck

La fórmula de la ecuación diferencial del proceso de Ornstein-Uhlenbeck es la base de su solución. Para resolver esta SDE, usamos la fórmula de la integración de factores. Vamos a reescribir la SDE:

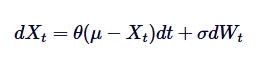
Primero, multiplicamos ambos lados por el factor de integración /upload/asset/28dfe9abfb54772651590.png:

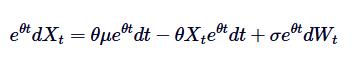
Tenga en cuenta que si sumamos 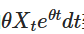a ambos lados, la izquierda puede representarse como la diferencia por el producto:

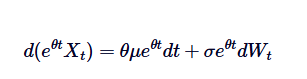
Integra ambos lados de 0 a t, y obtenemos:

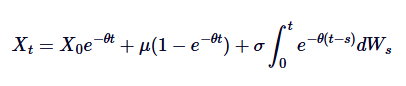
Esta es la explicación general de Ornstein-Uhlenbeck SDE.

La solución obviada derivada de lo anterior tiene varios significados importantes: el primer elemento 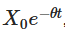indica que el valor inicial se desvanece con el tiempo, lo que indica cómo el proceso se olvida gradualmente de su punto de partida; el segundo elemento 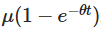indica que el proceso se orienta hacia el valor promedio de μ con el tiempo; el tercero elemento introduce la aleatoriedad, en la que la integral del proceso de Wiener explica la fluctuación aleatoria.

Esta solución enfatiza el equilibrio entre el comportamiento de regresión de la media de certeza y el coeficiente aleatorio impulsado por el movimiento de Brown. Comprender esta solución es fundamental para simular eficazmente el proceso de OU, como se describe a continuación.

Conexiones con otros procesos aleatorios

El proceso de Ornstein-Uhlenbeck tiene varias conexiones importantes con otros procesos aleatorios famosos (incluyendo el movimiento de Brown y el modelo de Vasicek).

Relación con el movimiento Brown

El proceso de Ornstein-Uhlenbeck puede ser visto como una versión de regreso a la mediana del movimiento de Brown. Un movimiento de Brown describe un proceso que tiene un incremento independiente y una tendencia a no regresar a la mediana, mientras que el proceso de OU introduce una regreso a la mediana mediante el uso de un derivado de derivación para modificar el movimiento de Brown, lo que lleva el proceso hacia el centro. Matemáticamente hablando, el proceso de OU se simplifica a un movimiento de Brown estándar con una banda oscilante si establecemos que θ = 0:

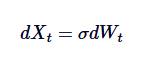
Por lo tanto, el movimiento de Brown es un caso particular del proceso OU, que corresponde a la ausencia de la regresión de la media.

Relación con el modelo Vasicek

El modelo de Vasicek es ampliamente utilizado en la modelación de tasas de interés, y es esencialmente una aplicación del proceso de Ornstein-Uhlenbeck en la evolución de las tasas de interés. El modelo de Vasicek asume que las tasas de interés siguen el proceso OU, donde la SDE se define como:

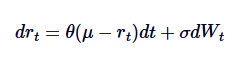
Entre ellos, rt representa la tasa de interés a corto plazo, y la interpretación de los parámetros θ, μ y δ es similar a la de la OU. La capacidad del modelo Vasicek para generar la trayectoria de la tasa de interés de regreso al promedio es una de sus principales ventajas en la modelación financiera.

El conocimiento de estas relaciones permite comprender más ampliamente cómo se utiliza el proceso OU en diferentes entornos, especialmente en el ámbito financiero. Exploraremos el significado práctico de estas conexiones al discutir ejemplos de aplicaciones a continuación.

Simulación del proceso Ornstein-Uhlenbeck en Python

En esta sección, vamos a explorar cómo usar Python para simular el proceso Ornstein-Uhlenbeck (OU). Esto implica el uso de la dispersión de Euler-Maruyama para dispersar la ecuación de diferenciación aleatoria (SDE) que define el proceso OU.

Descentralización de las SDE

Revisemos las fórmulas matemáticas de SDE arriba y resumamos cada término:

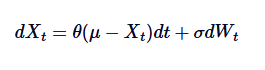
en,

• Xt es el valor del proceso en el tiempo t.
• θ es la velocidad a la que regresa el valor medio.
• μ es el promedio a largo plazo del proceso.
• δ es el parámetro de la tasa de fluctuación.
• dWt representa el incremento del proceso de Wiener (movimiento estándar de Brown).

Para simular este proceso en el ordenador, necesitamos una dispersidad del SDE de tiempo continuo. Un método común es la dispersidad de Euler-Maruyama, que se aproxima al proceso continuo teniendo en cuenta el pequeño paso de tiempo de dispersidad /upload/asset/28db85708af6d062dda8d.png. La forma dispersada del proceso de Ornstein-Uhlenbeck se da por la siguiente fórmula:

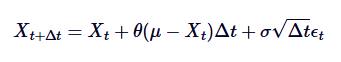
De ellos, 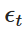es una variable aleatoria extraída de la distribución normal estándar (es decir, 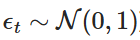). Esta dispersión nos permite calcular el valor de Xt en forma iterativa con el tiempo y así simular el comportamiento del proceso OU.

Implementación de Python

Ahora vamos a implementar el proceso Ornstein-Uhlenbeck descentralizado en Python. En este contexto, solo usamos NumPy y la biblioteca de Python Matplotlib.

En primer lugar, importamos NumPy y Matplotlib de manera estándar. Luego, asignamos todos los parámetros para el modelo OU. Luego, asignamos previamente una matriz NumPy de longitud N para agregarla después de calcular el camino OU. Luego, iteramos N-1 (el paso 1 es la condición inicial X0 especificada), simulamos el incremento aleatorio dW, y luego calcula la siguiente iterada del camino OU de acuerdo con la fórmula matemática anterior.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

El resultado de la cartografía es el siguiente:

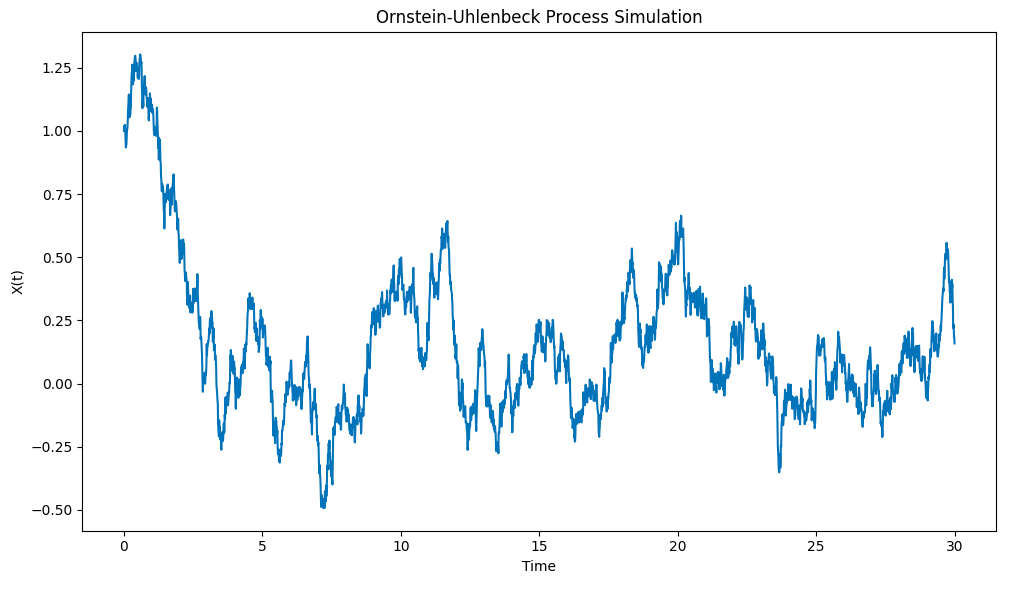
Simulación del proceso de Ornstein-Uhlenbeck dibujado con Python

Observe cómo el proceso se aleja rápidamente de la condición inicial para extraer el átomo X0 = 1 al promedio μ = 0, y luego muestra una tendencia a regresar a ese promedio cuando se aleja de ese promedio.

Resumen y pasos a seguir

En este artículo, resumimos el proceso de Ornstein-Uhlenbeck, describimos sus fórmulas matemáticas y ofrecemos una implementación básica de Python para simular una versión discreta de un SDE de tiempo continuo. En los siguientes artículos, estudiaremos los SDE más complejos construidos sobre el proceso OU y veremos cómo se utilizan en aplicaciones de transacción de sistemas y precios de derivados.

El código completo

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Enlace al artículo original: https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/