La historia de “escapar” y “sobrevivir” en el juego y la inversión
 1
1
 2876
2876
La historia de “escapar” y “sobrevivir” en el juego y la inversión
** Hablando de apuestas e inversiones, la gente generalmente está ansiosa por aprender los trucos para ganar dinero, de hecho, creo que ganar dinero no es fácil de aprender, requiere experiencia y sabiduría. Los principiantes que desean mejorar rápidamente su nivel deben practicar una buena defensa primero. No se trata de enseñar a los niños a faltar a la escuela, sino de explorar la ciencia de la fuga de la escuela con los compañeros de clase y compañeros de clase. Inspirado en una entrevista que hice hace tres años con el semanario de bolsa de valores Red Week de Liu Xiaobo. Bajo la guía de los periodistas, expuse mis profundas ideas sobre el negocio de las inversiones y las transacciones, publiqué un gran ensayo sobre la situación financiera de la economía mundial y, por cierto, hablé de algunas ideas de transacciones.
- ### El secreto de la fuga de la madre de Fang Yang, el principal manipulador de Wall Street
Un poco deprimido.
Sin embargo, cuando lo pienso detenidamente, tengo que admirar la agudeza de la redacción del periodista. La forma en que los inversionistas estadounidenses ganan dinero está un poco alejada de los ciudadanos chinos, y el panorama de la situación no es peor que el mío.
El maestro Wu Qiang puede comenzar con un cuento de misterio de Lord Yang y hacer un cuento de misterio de aprendizaje siguiendo el camino de Holmes, o puede comenzar con un cuento de misterio de fuga y desarrollar un cuento de misterio de escape. La entrevista de más de mil palabras de Wu en el semanario Liu Hong comenzó, y ahora vamos a hablar.
Primero saludo: mis pensamientos se desvían, si no estoy lejos, me perdonarán.
Recientemente descubrí que la parte que más le interesó a muchos lectores sobre el mundo de los juegos de azar de Wall Street fue la parte inicial sobre el juego ((Anteriormente, los comerciantes de Londres enviaron una versión electrónica a los amigos que dejaron su buzón de correo, con la esperanza de ayudar a todos). Parece que el punto 21 después de todo está más cerca de la masa que la caída de las tasas de interés.
Lo más importante es estar vivo.
Hablando de apuestas e inversiones, la gente suele estar ansiosa por aprender los trucos para ganar dinero, de hecho, personalmente creo que los métodos para ganar dinero no son fáciles de aprender, requieren mucha experiencia y conocimiento. Para los principiantes, mejorar rápidamente los niveles de apuestas, es mejor centrarse en practicar la defensa. La defensa es un conjunto de formas que se pueden aprender. En mi opinión, el requisito previo para el éxito de las apuestas e inversiones es hacer una buena defensa, guardar el dinero y luego esperar pacientemente la oportunidad real.
En resumen, no hay que sacrificar antes de que la revolución triunfe. No es fácil de hacer, sin mencionar que a nuestro alrededor hay muchos amigos y socios que se han enriquecido y han intentado morir antes que nosotros, incluso entre los mejores de la industria de la inversión, hay muchos que han caído de la cima.
A continuación algunos ejemplos:
Jesse Livermore: el personaje principal del libro de memorias de la bolsa de valores, el genio de la especulación, que comenzó de nada y llegó a tener un patrimonio de 100 millones de dólares en 1929, finalmente se declaró en bancarrota y se suicidó años después.
John Merryweather: Supertrader de la compañía de inversiones de los hermanos Solomon, quien creó el fondo de cobertura de capital de largo plazo de Star Wars (LTCM), que en su momento tenía un capital de 4 mil millones de dólares, pero que casi se perdió en la crisis de bonos de Rusia en 1998.
En 1988 fundó la bolsa de valores de la nación, que fue conocido como el padre de la bolsa de valores de China, pero en 1995 perdió el éxito en el caso de la deuda pública de 3.27 y quedó atrapado.
Tang Wanxin: El antiguo grupo de empresas de la familia Dron, arrogante en el mercado de capital chino, finalmente se desmoronó debido a la ruptura de la cadena de capital que provocó el derrumbe del imperio Dron.
Todos estos son genios de los mercados de capitales, pero al final han fracasado. Su experiencia nos dice que si no controlamos el riesgo, ocurrirá lo mismo que en el caso de los pescadores y los peces dorados: luchar por ser papa y volver a la cabaña junto al mar.
Lo más importante es estar vivo.
No lo sé, no lo haré.
Hace muchos años, solía viajar en autobús de Chinatown, Nueva York, a Atlantic City en busca de dinero, con gente trabajadora que trabajaba en las mesas de los restaurantes. La mayoría de ellos trataban de cambiar su destino en los casinos, pero a menudo se les pagaba un salario insignificante. Recuerdo que una vez, una chica de mi vecindario dijo que iba a jugar al casino todas las semanas y que tenía un juego de cartas secretas para ganar dinero.
En el camino de regreso, yo gané 800 dólares, y ella perdió 4000. De repente, me emocioné mucho, los 4000 dólares deberían ser su ingreso de más de un mes! Mirando el coche lleno de compatriotas sencillos vestidos, de repente me sentí muy triste, odio a los que hacen el negocio de hacer dinero, es como enviar a las ovejas a la boca del tigre! Traté de decirle a la chica que jugaría al lotería por mucho tiempo, pero ella no lo creyó, dijo que esta vez era solo mala suerte, y que volvería a leer el libro la próxima semana.
No tengo palabras, muchos fracasados usan la suerte como excusa.
Una victoria perdida es realmente una suerte, 10.000 derrotas ganadas son una teoría matemática (el que tiene más probabilidades de ganar casi siempre gana). En los juegos de casino donde los jugadores juegan con la probabilidad de ganar, ¿no es solo una cuestión de tiempo perder? Por lo tanto, hay un dicho: el casino no teme que ganes, sino que teme que no vengas.
Lo mismo ocurre con las inversiones.
El mercado bursátil es mejor que el casino, y en el largo plazo debería ser un juego de ganancias positivas. Sin embargo, debido a factores como el juego de cartas, el comercio interno y el impuesto de estampado, el inversor común y corriente tiene dificultades para ganar en el mercado si juega con demasiada frecuencia, e incluso puede perder por mucho tiempo.
En la época de la Edo, un espadachín japonés, Shigeru Miyamoto, había luchado en duelo con más de sesenta personas y nunca había sido derrotado. Además de su excelente habilidad, también tenía un secreto: nunca pelear con alguien que era más fuerte que él.
No lo sé, no lo haré.
Este es el primer consejo que los hackers y los inversores deben tener en cuenta.

¿Cuáles son las ventajas de los casinos?
El casino no tiene miedo de que ganes, sólo tiene miedo de que no vengas, porque los juegos de casino son básicamente juegos de azar. Muchos jugadores creen en la suerte, mientras que los que operan los casinos creen en la probabilidad, que es la diferencia entre el perdedor y el ganador.
Por ejemplo, en la ruleta (ver la imagen de abajo), los jugadores pueden apostar en cualquier número, y si la bola en el rollo se detiene en ese número, el casino gana 35 veces.
Suena muy tentador, ¿verdad?
El joven de la película Casablanca, que escapó de Europa, fue detenido 22 veces y luego pagó el viaje a los Estados Unidos. ¿Cuál es la realidad?
¿Qué es lo que está pasando?
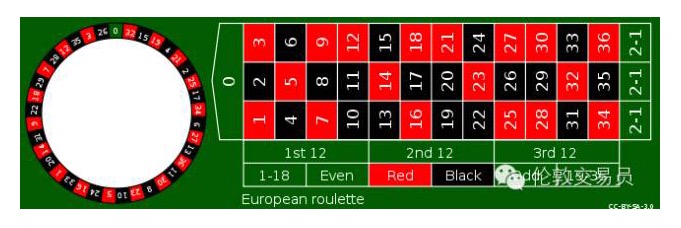
Si sólo 1-36 estos 36 números, entonces el jugador cada apuesta de 1 dólar, en promedio cada 36 gana una vez, 35 dólares ganados justo compensar el otro 35 de pérdida de dinero. Pero el casino añadió una moneda 0 a la izquierda de la ruleta, la cara de ganancia del jugador se convirtió en 1⁄37, ganando 35 dólares no es suficiente para compensar el otro 36 de pérdida de dinero, el casino ocupa 1⁄37 = 2,70% de la ventaja de probabilidad, es decir, cada jugador apuesta 100 dólares, el promedio de perder 2.7 dólares.
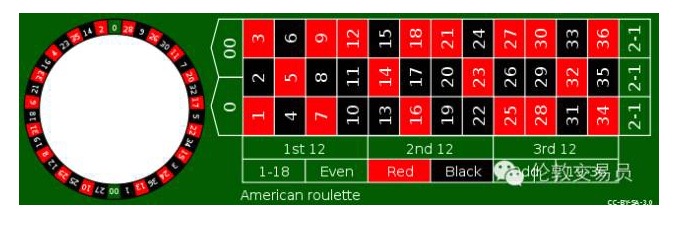
Aparte de apostar a números individuales, las cartas de ruleta también tienen otras opciones como apostar a rojo y negro. Tanto los números individuales de 1 a 35 como los números individuales de 1 a 1 en rojo y negro, la ventaja del casino es la misma. Pero hay una diferencia importante entre los dos: las fluctuaciones de pérdidas y ganancias de los números individuales son claramente más grandes que las apuestas en rojo y negro.
En primer lugar, un breve comentario: la ganancia y la volatilidad son dos de las cosas más importantes en el juego y la inversión.
En realidad, el juego de apuestas en las que el ganador de la lotería es seguro de perder es mejor que no se toque, ya que si se quiere jugar, hay que elegir entre la volatilidad de ganar y la de perder; en cambio, las inversiones en las que el ganador de la lotería es seguro de ganar deben elegir la volatilidad de ganar y la de perder.
Volviendo a los juegos de azar, la mayoría de los juegos de casino están diseñados de manera similar a los juegos de ruleta: los casinos tienen una ventaja de probabilidad. En estos juegos, los jugadores pueden ganar dinero con suerte si solo juegan unas pocas manos, y casi siempre pierden si juegan por mucho tiempo, lo que en matemáticas se llama la ley de los grandes números.
Sin embargo, los matemáticos han encontrado un hueco en el cálculo de las máquinas de casino.
Historias antiguas de las 21
A principios de la década de 1960, un matemático estadounidense llamado Edward Thorp utilizó una nueva computadora para encontrar oportunidades en el juego de 21 puntos y desarrolló un método para derrotar al casino mediante el conteo de cartas. El profesor Thorp aplicó la teoría en la práctica, y con su propio método de conteo de cartas, incluso ganó un gran casino, y pronto fue incluido en la lista negra.
El libro de Thorpe, Beat the Dealer, vendió 700.000 ejemplares y fue el libro más vendido en el New York Times, recordando a la misma persona que hizo un gran lío en Wall Street, el autor se avergonzó… y los ingresos por derechos de autor fueron mucho mayores que los ingresos de los juegos de azar.
El principio de contar cartas de Thorpe no es difícil. En primer lugar, la regla de los 21 puntos: el jugador y el crupier (casino) se enfrentan para ver quién tiene la suma de los puntos de las cartas más cerca (pero no más) de los 21 puntos. 10, J, Q, K cuentan con diez puntos, y los números de 2 a 9 se cuentan en función de sus respectivos puntos.
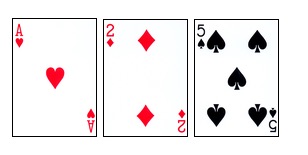
El juego de cartas comienza cuando el jugador y el crupier reciben dos cartas cada uno, y las cartas del crupier son claras y oscuras (como se muestra a continuación). Luego, el jugador toma una decisión: puede agarrar cartas, hacer acciones especiales como doblar, o optar por detener el juego en cualquier momento. Si el jugador supera los 21 puntos (explosión), pierde directamente, de lo contrario, se detiene y luego pasa a la acción del crupier.
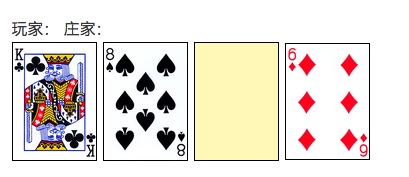
Además, hay una regla especial: una carta A y una carta de diez puntos ((10, J, Q, K) se llaman Black Jack (Blackjack), y el ganador gana directamente. Si el jugador obtiene un Black Jack, puede ganar 1.5 veces el chip. Si el casero obtiene un Black Jack, solo puede ganar 1 veces el chip.
Es evidente que el casero y el jugador tienen una ventaja en el juego de 21 puntos. La ventaja del casero es que el jugador puede ganar sin pelear si el jugador se deshace primero. La ventaja del jugador es que puede moverse con flexibilidad y decidir su estrategia según su propia carta y la carta que el casero revela. Además, las probabilidades de blackjack 3:2 también favorecen al jugador.
Cuanto más cartas de diez puntos y A, más probabilidades de blackjack, más fácil es el golpe, y la ventaja de que el jugador se mueve y se mueve de manera flexible es más valiosa. Por el contrario, cuanto más cartas pequeñas como 3, 4, 5, 6 y así sucesivamente, menor es la probabilidad de golpe, es más favorable para el casero.
En la era de Thorpe, los 21 se ganaban con una o dos cartas de póquer, y cuando las cartas se lavaban, el casino tenía una ventaja de probabilidad de alrededor del 0,5%. Lo curioso es que, a medida que avanzaba el juego de cartas, a veces la proporción de cartas grandes y A aumentaba, y la probabilidad se convertía en una ventaja para el jugador.
Un monje llamado Thorpe inventó el juego de cartas, escribió un libro que fue un éxito de ventas, luego se dio cuenta de que Wall Street se había enriquecido, y luego se hizo un mundo en el mundo de los fondos de cobertura. ¡Alguien llamado Thorpe también!
En cuanto al casino, desde entonces ha surgido un grupo de contadores de cartas que han dominado a los contadores de cartas de Sochi. En el casino, los contadores de cartas intentan hacer todo lo posible para rechazar a los jugadores de cartas fuera de la puerta, y los jugadores de cartas buscan soluciones para romper el bloqueo.
(Tenga la seguridad de que la historia contada al final siempre regresará a la inversión).
El equipo de MIT
Hablando de Thorpe, el casino tuvo problemas para atrapar a los jugadores de cartas. Con el tiempo, el casino acumuló una lista negra. Si la persona en la lista era reconocida en la mesa de 21 cartas, por lo general, era enviada de inmediato a la frontera con el regalo: ¡Vayan a jugar a otra parte!
En una época de la década de los ochenta, los detectives contratados por el casino analizaron las listas negras que habían recopilado y descubrieron una pista importante: muchas de las direcciones de los jugadores de cartas estaban cerca de Cambridge, Massachusetts. Cambridge, Massachusetts, tal vez no lo hayas oído, pero no es posible que no hayas oído hablar de las dos universidades ubicadas en esta ciudad: Harvard y el Instituto de Tecnología de Massachusetts.
La verdad fue saliendo a la luz, y un grupo de jugadores de cartas, en su mayoría estudiantes de MIT, se unieron a la causa.
Esta es una organización que opera con maquillaje comercial: hay alguien que crea el capital, alguien que administra, alguien que juega las cartas, todo el equipo de inversión y el equipo de control de riesgo del equipo de la modalidad del fondo de cobertura. El mayor beneficio de la trama de la trama de la trama de la trama de la trama es que se puede evitar el riesgo que enfrenta el pirata individual: la volatilidad de ganar y perder es grande: 21 puntos, más alta sea su técnica, la mala suerte en el corto plazo también puede perder el capital, la operación del grupo puede dispersar este riesgo. Además, los piratas del MIT también utilizan algunas técnicas de la trama de la trama de la trama.
Por ejemplo, Michael, quien contaba las cartas, lanzaba las criptomonedas preestablecidas en cada apuesta pequeña cuando la situación era favorable, mientras que James, que se hacía pasar por el menor, venía y jugaba con una apuesta de 1000 dólares.
El grupo del MIT ha estado operando por más de una década, con la participación de instituciones como el MIT y Harvard, entre ellos un chino que ganó una medalla de oro en los Juegos Olímpicos. Los soldados que se deshacen de los botines de hierro, de todos modos, el más importante en Cambridge, Massachusetts, son los genios de las matemáticas.
A mediados de los noventa, la economía estadounidense estaba en auge, los miembros de la pandilla viajaban a Silicon Valley, Wall Street y otros lugares, y la pandilla de MIT se fue dispersando. Esto también parece demostrar una verdad: los jóvenes tienen un buen trabajo, y la tasa de delincuencia disminuye.
Unos años más tarde, un compañero de clase chino de la escuela de pescadores encontró por casualidad el juego de cartas de 21 puntos, y me interesó mucho. En ese momento, no había oído hablar de Soup, ni sabía que el libro de Soup vendía solo una docena de dólares por libro, y gasté 100 dólares en comprar el llamado libro de secretos de cocina a un gran perdedor llamado Kadosa.
Pero el lago no es el lago de ese año.
La confusión sobre las apuestas
Después de aprender a contar cartas, fui con entusiasmo a Las Vegas para probar el cuchillo. El resultado fue muy bueno, gané una gruesa pila de cien dólares, que es una verdadera mina de oro. ¡Vivo en Nueva York, no puedo ir siempre a Las Vegas para cavar oro, porque cerca de Nueva York también hay la segunda ciudad más grande de los Estados Unidos, Atlantic City, así que me convertí en un cliente habitual allí!
Después de un tiempo de juego, me di cuenta de que Atlantic City no era un buen lugar para elegir, que en general sólo podía ganar poco y que había mucha volatilidad en las ganancias y en las pérdidas. Después de estudiar detenidamente, descubrí que Atlantic City no era como Las Vegas.
Como se mencionó anteriormente, los jugadores de cartas se basan principalmente en la proporción de cartas grandes y pequeñas en el resto de la carta, y apuestan mucho cuando la proporción de cartas grandes es más alta de lo normal.
Evidentemente, la proporción es más fácil de aumentar en dos situaciones, la primera es cuando no hay muchas cartas restantes, y la segunda es cuando el juego de 21 puntos solo usa 1-2 cartas de segunda mano. El juego de 21 puntos de la era Thorpe tiene estas dos características: solo usa 1-2 cartas de segunda mano, y el crupier casi lava las cartas con la luz, por lo que la proporción de las cartas grandes siempre es alta, y los jugadores de cartas tienen muchas oportunidades de apostar cuando la situación es favorable.
Naturalmente, en el casino también hay gente de alto nivel que planea cosas, ya que la mejor defensa suave para el recuento de cartas es tratar de controlar la fluctuación de la proporción de cartas grandes y pequeñas, por lo que el casino hace dos medidas tóxicas. La primera es aumentar el uso de cartas de 21 puntos, cambiando de 1-2 pares a 6-8 pares.
Es obvio que, con una sola carta, la proporción de cartas grandes y pequeñas no cambia fácilmente.
El segundo es el lavado de cartas temprano, para evitar la situación en la que la proporción es más susceptible a la fluctuación. Las casas de juego de Las Vegas son numerosas y muy competitivas, y las casas de juego reservan algunos juegos de 21 puntos de 1-2 cartas secundarias para los jugadores de azar.
El lago de mi madre ya no es el lago de Thorpe.
Sin embargo, aunque la proporción sea más alta, también tengo ventajas en el casino. Anteriormente hablé de la ley de la mayoría de la lotería: siempre que haya una ventaja, en teoría, siempre juego al final o gano. Pero la teoría a la teoría, en la práctica hay una restricción importante: mi apuesta es limitada, no puedo jugar si pierdo. La ley de la mayoría solo dice que la revolución de la lotería finalmente ganará, pero no garantiza que no sacrifique la lotería antes de la victoria de la revolución de la lotería.
Supongamos que sólo gané $10,000, no sería fácil esperar hasta que tuviéramos una ventaja de probabilidad del 1% sobre el casino.
Place your bets. (Ponga sus apuestas)
¿Cuánto apuesto? 20 dólares? El promedio es de 2 centavos, no lo entiendo. ¿Apuesto 2000 dólares?
Me quedé sin luz cuando alcancé a un cisne que no era muy negro (perdí 5 en fila). Parece que 20 dólares es demasiado poco, 2000 dólares es demasiado, y la mejor apuesta debería estar entre ambos. ¿Cuánto debería apostar?
Una persona de alto rango ya ha dado la respuesta.
(Vamos a hablar de la teoría de la inversión).
Fórmula de Kelly
En 1956 el científico John Kelly publicó un artículo en el que proponía la famosa fórmula de Kelly.
f* = (bp - q) / b Donde f* = porcentaje de la cantidad invertida en el capital total p = probabilidad de ganar q = probabilidad de fracaso, q = 1-p b = probabilidad, por ejemplo, apostar un solo número en la ruleta, b = 35, apostar en rojo y negro, b = 1。
En el problema de las 21 apuestas mencionado en el artículo anterior, suponiendo que el total de ganancias sea de $10,000, y que la probabilidad de que el jugador gane sea del 51%, con una probabilidad de 1:1 (la probabilidad real de ganar y la probabilidad de perder están ligeramente desviadas, pero no muy lejos), entonces la mejor apuesta dada por la fórmula de Kelly es:
\(10000 * (1 * 0.51 - 0.49)/ 1 = \)200 Sé que muchas personas se asombran al ver las fórmulas matemáticas, pero para jugar y invertir no hay manera de no usar las matemáticas. Lo más importante no es calcular los números con las fórmulas, sino entender el verdadero significado detrás de las fórmulas.
En primer lugar, bp - q de la molécula en la fórmula representa que el ganador gana el ganador, en matemáticas se llama el ganador del valor esperado, y la fórmula de Kelly indica que se puede apostar solo en juegos con un valor esperado positivo, que es la verdad más básica de todos los juegos de azar e inversiones, es decir, el ganador de la fórmula anterior no tiene certeza y nunca apuesta.
En segundo lugar, la ventaja es la proporción de dinero invertido dividido por la ventaja b. Es decir, si la ventaja es la misma, las probabilidades son más pequeñas y se puede apostar más. Esto no es fácil de entender intuitivamente, y lo ilustramos con un ejemplo.
La probabilidad de ganar es del 20%, ganando 1 y perdiendo 5 y perdiendo todo el juego.*20% - 80% = 20% La probabilidad de ganar es del 60%, 1 a la baja 1 ⋅ bp - q = 1*60% - 40% = 20% Las apuestas grandes y pequeñas: ganancias del 80%, pérdidas del 1 0.5 ◦ bp - q = 0.5*80% - 20% = 20%
Los tres juegos tienen el mismo valor esperado matemáticamente, es el 20%, o sea, apuesta 100 dólares y gana 20 dólares en promedio. De acuerdo con la tenacidad de la mayoría de los países, tal vez se elija el juego de lotería grande y pequeña, ¿verdad?
En realidad, la mayoría de los que juegan a los juegos de azar son piratas.
¿A quién le gusta jugar a las loterías? ¡Al casino!
Los inversionistas profesionales de Wall Street también juegan mucho a las apuestas grandes y pequeñas, ya que son más fáciles de usar para apalancarse.
Finalmente, la fórmula de Kelly señala la importancia de controlar el riesgo: incluso en juegos con un valor esperado positivo, no se puede apostar demasiado. Matemáticamente hablando, la proporción de dinero apostado supera el valor de Kelly, y la velocidad de ganancia de dinero a largo plazo, en cambio, disminuye y aumenta considerablemente la probabilidad de sufrir pérdidas catastróficas. Por ejemplo, en un caso extremo, si apuestas todo el dinero de cada mano, no importa cuánto dinero ganes, perderá la fortuna inmediatamente.
¿Por qué el mundo de los inversores ha perdido su fortuna a manos de algunos expertos en tecnología local? La razón es que la mayoría de ellos están apostando demasiado dinero.
Livermore fue derrotado por Mill City.
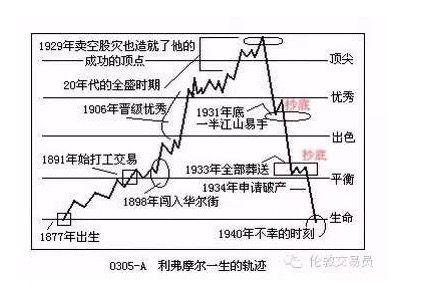
El 28 de noviembre de 1940, 16 años después de la aparición de la fórmula Kelly, un soltero que había vivido en la calle Wall Street sacó una pistola de su armario en el Waldorf Hotel de Nueva York, dejando una nota a su esposa: “Oh… estoy cansado de luchar… esta es la única liberación.
Jesse Livermore, el personaje de la famosa autobiografía de Jesse Livermore, murió de una forma muy triste.
Si aún no has leído Reminiscences of a Stock Operator, te recomiendo que lo hagas. Muchos gestores de fondos de cobertura de clase mundial han admirado este libro. Siguiendo los altibajos de la vida del protagonista, puedes vislumbrar el estilo de los mercados financieros estadounidenses, turbulentos y vibrantes, hace más de un siglo, y sorprenderte de que el mundo haya favorecido a un genio como Fermor.
En la era de los primigenios, resumió muchas de las reglas que los inversores modernos consideran clásicas: ganar dinero con dinero, perder dinero con pérdidas, no tomar a la ligera las opiniones de los demás o las llamadas “informaciones privilegiadas” y un conjunto completo de reglas para los inversores modernos.
Lo que es más impresionante es que Livermore no sólo era un teórico, sino también un practicante. Su vida de negocios fue muy variada, desde un negocio de manos de nadie que le valió millones de dólares en 1907 hasta un negocio de 100 millones de dólares en 1929! En ese momento, los automóviles se vendían por solo unos cientos de dólares cada uno, y los 100 millones de dólares que Livermore obtuvo de las transacciones equivalían a más de 10 mil millones de dólares de hoy!
Este genio no reconocido, que luego perdió una gran fortuna en el mercado, terminó representando la triste escena que comenzó este artículo. ¿Cómo salió Livermore de Macquarie? La documentación no es específica, pero si se analizan cuidadosamente sus hábitos de negociación, no es difícil encontrar huellas.
Livermore comenzó su carrera como comerciante en Bucket Shop.
A finales del siglo XIX, los mercados de valores estadounidenses estaban muy activos, y los avances tecnológicos también permitieron a la gente común de Nueva York participar en especulación bursátil en tiempo real: las máquinas de cotización automáticas conectadas a cables de telégrafo podían transmitir los últimos precios de transacción de la Bolsa de Nueva York a todo el país. En ese momento, muchas personas querían participar en especulación, pero carecían de fondos para comprar y vender acciones, y los ladrones aprovecharon la oportunidad para atraer a esta multitud a los casinos bursátiles.
Hay máquinas automáticas en los casinos que hacen que los jugadores parezcan estar negociando acciones, que en realidad son del tamaño de una piña. Por ejemplo, la última oferta de una acción es de 80 dólares, y el jugador puede comprar una piña con solo pagar un bono de 1 dólar. Si el precio aparece en la máquina de 79 dólares o menos, perdemos la luz; si el precio es de 81 dólares, el jugador puede ganar 1 dólar de ganancias, o seguir adelante.
¿Cómo ganan los ladrones de los casinos de la bolsa?
Además de aprovecharse de la característica de que las multitudes a menudo apuestan mal, también conspiran con algunos corredores para manipular el mercado. Por ejemplo, con un precio de 80 dólares, muchos jugadores apuestan el gran bono, los corredores de casino indican a sus compañeros de la bolsa de Nueva York que presionen el precio de las acciones, y el casino se queda con el gran bono apostado con tan solo un precio de 79 dólares en la máquina de cotización automática.
Cuando era joven, Livermore no tenía mucho dinero, se mezcló en el casino de acciones y poco a poco aprendió a predecir el precio del mercado basándose en las ofertas (Read Tape). En ese momento no había computadoras, ni gráficos de K en tiempo real, y el Kung Fu de Livermore era realmente el prototipo del análisis técnico.
Pero sospecho que también ha desarrollado el mal hábito de jugar en el casino de la bolsa: las apuestas son demasiado grandes.
Desde el punto de vista de la fórmula de Kelly, la garantía ultrabaja en los casinos de acciones es en realidad el asesino de los jugadores. El apalancamiento es tan grande que se apuesta por mucho más que el mejor valor de Kelly, y la pérdida es tarde o temprano. La garantía de transacción en el mercado financiero formal de los Estados Unidos en ese momento también era baja.
El historial de sus operaciones es impresionante, las acciones, el algodón, la soya, todo lo que sea, es una operación de gran apalancamiento, lo que ha logrado el legendario éxito de Livermore y lo ha llevado a la bancarrota en varias ocasiones. Afortunadamente, con la ayuda de los nobles, Livermore pudo aprovechar varias oportunidades importantes para alcanzar el pico en 1907, 1915 y 1929.
Sin embargo, el hombre sabio se equivocó y, en última instancia, falló, y sospecho que fue el error de apostar demasiado lo que hizo que Livermore perdiera todo su dinero en pocos años después de alcanzar un valor de 100 millones de dólares.
¿Cuáles son las maravillas que este genio podría crear si combinara el método de administración de fondos de Livermore basado en la fórmula de Kelly con su habilidad para dominar el mercado?
La historia no tiene si.
Livermore ha pasado como un meteorito, tal vez ha vivido décadas más.
La teoría de la gestión de fondos y el control de riesgos no se formó hasta los años cincuenta.
La fórmula de Kelly señala que los juegos con grandes ganancias y poca volatilidad pueden apostar más. Entonces, ¿cómo cuantificar las ganancias grandes y poca volatilidad? Un académico contemporáneo de Kelly presentó un indicador famoso.
Proporción de Sharpe
En la década de 1950, se propuso utilizar la relación entre la expectativa de retorno y la volatilidad como un indicador para medir la oportunidad de inversión. En 1966, el académico William Sharpe propuso el famoso índice de Sharpe sobre esta base:
S = (R r) / σ, donde: R = retorno esperado de la inversión (retorno promedio) r = tasa de retorno de la inversión sin riesgo (que se puede entender como la tasa de retorno de la inversión en bonos estatales) σ = diferencia estándar de la tasa de retorno (el indicador estadístico más utilizado para medir la volatilidad)
El mayor índice de Sharpe S, mayor calidad de la oportunidad de inversión. Por ejemplo:
A Inversión: Exceso (más deuda pública) de retorno esperado de 10%, diferencia estándar de 20%, Sharpe ratio de 0.5 B inversiones: Expectativa de rendimiento superior al 5%, diferencia estándar del 5%, Sharpe ratio del 1
A primera vista, una inversión en A con expectativas de rendimiento altas parece una buena oportunidad. De hecho, la inversión en B es mucho mejor, ya que su índice de Sharpe es alto, lo que significa que el inversor puede intercambiar 1 unidad de riesgo de A por una mayor expectativa de rendimiento. La misma conclusión se puede extraer de la perspectiva de la inversión con apalancamiento: suponiendo que el inversor financie con una tasa de interés de préstamo r, duplicando el apalancamiento en la oportunidad de inversión en B, entonces la inversión en B con apalancamiento se convierte en una expectativa de rendimiento del 10% y una diferencia estándar del 10%, la misma expectativa de rendimiento que la inversión en A, mientras que el riesgo es menor.
¿Cuál es el índice de Sharpe para ser una buena jugadora?
Veamos un ejemplo práctico: la rentabilidad media anual a largo plazo de las acciones estadounidenses es de aproximadamente 10%, la volatilidad es de aproximadamente 16%, la rentabilidad sin riesgo es de aproximadamente 3.5%, por lo que la proporción de Sharpe es de aproximadamente 0.4 (fuente: Wikipedia).
El riesgo/retorno de invertir en acciones de EE.UU. es algo del pasado para los inversores minoristas de largo plazo. Si eres un gerente de fondos de cobertura, esa tasa de Sharpe es demasiado baja: suponiendo que tu objetivo sea un retorno anual del 20%, deberías usar 2.5 veces el nivel de apalancamiento (retorno esperado = 2.5).*10% - 1.53.5% ≈ 20%), significa que el promedio de 1 de cada 6 años de rendimiento será inferior a 2.5(10% - 16%)- 1.5*3.5% = -20% . Si pierdes más del 20%, el cliente probablemente se quedará sin dinero .
En general, el índice de Sharpe superior a 1 es un buen juego. Esta oportunidad no es frecuente en los juegos de inversiones simples, por lo que los inversores profesionales a menudo utilizan métodos de cobertura para modificar el juego de inversiones de Bitcoin y mejorar el índice de Sharpe.
Por ejemplo, si inventas una manera de cubrir una inversión de Sharpe ratio de 2 con una variedad de activos, y te atreves a usar el apalancamiento (los compañeros que saben matemáticas pueden calcular la probabilidad de perder dinero por sí mismos), los inversores probablemente seguirán a tu fondo de cobertura para invertir.
Sin embargo, el método de inversión de cobertura y apalancamiento suele tener un obstáculo: se requiere mucho dinero prestado y se requiere mucha liquidez, por lo que la crisis de emergencia suele ser un problema, como se analizó en el caso de LTCM y el fondo Global Alpha de Goldman Sachs en Wall Street.
La proporción de Sharpe también tiene sus defectos, ya que asume que el rendimiento es normal, mientras que la distribución real del rendimiento de la inversión tiene un cola de acebo (la probabilidad de perder mucho dinero es mayor que la estimación de la distribución normal), por lo que hay problemas para seleccionar oportunidades de inversión simplemente en función de la proporción de Sharpe y es fácil de manipular. Este tema no se discute aquí.
Para el inversor común, el índice de Sharpe sugiere que se debe considerar de manera integral desde el punto de vista del riesgo y el rendimiento, y elegir inversiones que sean más rentables que más altas. Este es el punto de vista mencionado en el artículo anterior: el juego de ganancias positivas debe elegir un juego de baja volatilidad, el juego de ganancias negativas debe elegir un juego de gran volatilidad si tiene que jugar. En resumen, cuanto mayor sea el índice de Sharpe, mejor.
La proporción de Sharpe habla de cómo elegir las cartas de juego, mientras que la fórmula de Kelly habla de cómo elegir las apuestas después de la partida para obtener la mejor tasa de retorno a largo plazo. Ahora vamos a combinar los dos métodos para ver si la tarjeta de 21 puntos es la mejor manera de hacer dinero.
Las instrucciones adicionales sobre la proporción de Sharpe
En cuanto a la proporción de Sharpe, las preguntas se centran en varios aspectos:
La primera pregunta es: ¿cómo se calcula que el rendimiento promedio de un año de aluminio por debajo del -6% en el caso de la bolsa de valores estadounidense?
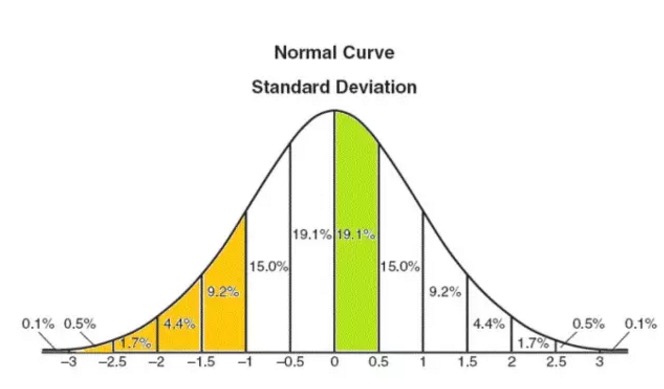
La proporción de Sharpe asume que el retorno de la inversión corresponde a una distribución normal (ver la imagen a continuación). Matemáticamente, la suma de un gran número de eventos aleatorios independientes generalmente corresponde a una distribución normal. Por ejemplo, el lanzamiento continuo de una moneda, el lado positivo es 1, el lado contrario es 1, el resultado de una gran cantidad de repeticiones corresponde a una distribución normal.
La hipótesis de la distribución normal, aunque imperfecta, es el marco básico para entender el problema. El siguiente gráfico muestra los valores de probabilidad de la distribución normal. Por ejemplo, la probabilidad de la tasa de retorno entre 0 y 0,5 veces la diferencia estándar es de 19.1% (la parte verde de la gráfica).
Del mismo modo, la probabilidad de que el rendimiento sea inferior a 1x el estándar de diferencia (la parte de color naranja en el gráfico) es de aproximadamente el 16% [2]. Se aplica a las bolsas de valores estadounidenses (el rendimiento medio es del 10%, el estándar de diferencia es del 16%) y la probabilidad de que el rendimiento anual sea inferior a 1x el estándar de diferencia, es decir, del 10% al 16% = -6%, es de aproximadamente 1⁄6.
La segunda pregunta es: ¿hay alguna discrepancia entre la hipótesis de la proporción de Sharpe y la realidad?
Por supuesto que sí. La hipótesis de una distribución normal no es perfecta. En realidad, el movimiento de la bolsa de valores no es completamente independiente de la curva aleatoria, de lo contrario no necesitaríamos preocuparnos de estudiar ninguna ley. Por ejemplo, en la crisis financiera, el movimiento de la bolsa de valores tiene una fuerte correlación de secuencia, la llamada curva de tendencia de la curva, que conduce a que los retornos reales de la bolsa de valores tengan el fenómeno de la curva de la cola de la cebolla, es decir, la probabilidad de que la curva corra hacia la posición extrema es mayor que la estimada de la distribución normal.
Además, la proporción de rendimiento sin riesgo de la tasa de Sharpe r es un concepto vago, y el costo de financiación de los inversores no es r. Además, el cálculo de la volatilidad no es una cuestión sencilla.
La tercera pregunta es: ¿qué utilidad tiene el Sharpe ratio para el inversor promedio?
La siguiente vez que alguien te diga que he tenido un retorno promedio del 30 por ciento en los últimos tres años, puedes preguntarle con timidez: ¿Cuánta volatilidad tiene el titanio? En el siguiente blog veremos un ejemplo real de un fondo de cobertura.
Ejemplos de análisis de los resultados de los fondos de cobertura
Para evaluar el rendimiento de las inversiones, no solo se debe considerar el rendimiento, sino también los factores de riesgo. Ahora veamos un ejemplo real de un fondo de cobertura. La siguiente tabla muestra el rendimiento promedio anual de varios de los fondos de cobertura más grandes conocidos.
Cuadro 1
| - | - |
| - | Rentabilidad anual combinada |
| Fondo A | 14.15% |
| Fondo B | 15.17% |
| Fondo C | 15.20% |
| Fondo D | 79.17% |
| Fondo E | 2.78% |
Usted elegiría el fondo D, que tiene un retorno anual del 79%, ¿verdad? Felicitaciones, usted eligió el Paulson Credit Opportunities Fund, que se puso en marcha en medio de la crisis financiera para hacer préstamos a corto plazo, recaudar miles de millones de dólares en ganancias y salir de riesgo. Paulson, quien creó y administró el fondo (el mismo nombre que el ex ministro de finanzas de los Estados Unidos, Paulson, pero sin parentesco) también se convirtió en uno de los gerentes de fondos más famosos.
Pero ya hemos hablado: no se puede ver solo la rentabilidad sino también el riesgo. La tabla 2 muestra la volatilidad de los fondos y la valoración del Sharpe ratio (suponiendo una rentabilidad sin riesgo del 3%). ¿Qué piensas después de ver esto?
Cuadro 2
| - | Rentabilidad anual combinada | Variabilidad de las tasas de retorno | Proporción de Sharpe |
|---|---|---|---|
| Fondo A | 14.15% | 5.94% | 1.9 |
| Fondo B | 15.17% | 12.30% | 1.0 |
| Fondo C | 15.20% | 4.53% | 2.7 |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 |
| Fondo E | 2.78% | 12.21% | <0 |
En otras palabras, la volatilidad del fondo C es solo un décimo de la de los fondos Paulson, suponiendo que el inversionista solo esté dispuesto a asumir un riesgo de volatilidad fija, entonces puede invertir 1 dólar en un fondo Paulson o 10 dólares en un fondo C, con un riesgo similar, pero con un rendimiento total más alto en el fondo C.
El fondo C es Millennium Intl Ltd, el árbol perenne de la industria de los fondos de cobertura, cuyos gerentes han tenido varios altos funcionarios de origen chino. Desde el punto de vista de los inversores, es un poco difícil elegir entre un fondo Paulson exitoso o un fondo Millennium sólido. Además, el índice de Sharpe de los fondos A y B es claramente superior al 0.4 de la bolsa estadounidense, y es una buena opción de inversión.
En un análisis más detallado, comparar sólo con la tasa de Sharpe parece ser un poco injusto para las ganancias de los fondos Paulson: aunque es muy volátil, es principalmente una ganancia que fluctúa hacia arriba, una ganancia que fluctúa en el proceso de ganancias, en realidad no es un riesgo. Los inversores temen perder dinero, especialmente si pierden varias décadas.
Cuadro 3
| - | Rentabilidad anual combinada | Variabilidad de las tasas de retorno | Proporción de Sharpe | La mayor caída (cuándo ocurrió) |
|---|---|---|---|---|
| Bluecrest | 14.15% | 5.94% | 1.9 | -4.83% (2003) |
| FORE (capital de la línea de frente) | 15.17% | 12.30% | 1.0 | -27.01%(2008) |
| El milenio | 15.20% | 4.53% | 2.7 | -7.24% (1998) |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 | -10.41%(2007) |
| Drake | 2.78% | 12.21% | <0 | -51.74%(2007-2009) |
Ahora es más interesante que el fondo A (Bluecrest Capital) haya tenido su mayor caída de menos del 5% y que ocurriera en el 2003. El fondo evitó grandes pérdidas en la gran crisis de 2007-2008, lo cual es bastante atractivo. Bluecrest y Millennium son del tipo que se mantienen firmes y evitan la crisis de subpréstamos, y parece que no hay diferencia entre los dos.
En comparación con los fondos de Paulson, se puede decir que los tres fondos son favoritos de los inversores institucionales, con fondos administrados de 8.6 millones de dólares, 10 millones de dólares y 6.3 millones de dólares respectivamente. Parece que es lógico que la gente pueda hacer grandes cosas.
El fondo E (Drake Absolute Return Fund) también era un gran fondo que administraba miles de millones de dólares, pero sufrió una gran pérdida de más del 50% durante la crisis financiera, lo que hizo que los inversores perdieran la confianza y se retiraran, por lo que el capital administrado por Drake ahora es de solo $ 200 millones.
Finalmente, el fondo B, con un rendimiento anual compuesto a largo plazo del 15%, un índice de Sharpe 1, un buen índice de composición, aunque sufrió una pérdida del 27% en 2008, ha superado la crisis. Se puede decir que el fondo B tiene una gran fuerza, por lo que también se convirtió en un gran fondo que administra miles de millones de dólares. El nombre del fondo es FORE Capital, y el asesor Matthew Li es una bandera de los chinos en el mundo de los fondos de cobertura.
A partir de este ejemplo real de la evaluación de la rentabilidad de las inversiones, podemos ver la utilidad de los indicadores de riesgo como el índice de Sharpe y la caída máxima. Los inversores principiantes a menudo tienen el problema de considerar solo los retornos y no ver el riesgo.
¡La información proporcionada es solo para referencia y no constituye una recomendación de inversión!
Sin embargo, la mayoría de los bloggers no están de acuerdo.